Matematyka

Matematyka to nauka o liczbach, kształtach i wzorach. Słowo to pochodzi od greckiego słowa "μάθημα" (máthema), oznaczającego "naukę, wiedzę lub uczenie się", i czasami jest skracane do matematyki (w Anglii, Australii, Irlandii i Nowej Zelandii) lub matematyki (w Stanach Zjednoczonych i Kanadzie). Te krótkie słowa są często używane przez uczniów i ich szkoły do arytmetyki, geometrii lub prostej algebry.

Matematyka obejmuje badania:

Liczby: jak można liczyć.
Struktura: jak wszystko jest zorganizowane. To podpole jest zwykle nazywane algebrą.
Miejsce: gdzie są rzeczy i ich układ. To podpole jest zwykle nazywane geometrią.
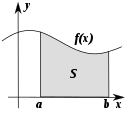
Zmiana: jak rzeczy stają się inne. To podpole zazwyczaj nazywane jest analizą.

Matematyka jest przydatna w rozwiązywaniu problemów występujących w realnym świecie, dlatego wiele osób oprócz matematyków studiuje i korzysta z matematyki. Dziś część matematyki jest potrzebna w wielu zawodach. Ludzie pracujący w biznesie, naukach ścisłych, inżynierii i budownictwie potrzebują trochę wiedzy z zakresu matematyki.

Rozwiązywanie problemów w matematyce

Matematyka rozwiązuje problemy za pomocą logiki. Jednym z głównych narzędzi logiki używanych przez matematyków jest dedukcja. Dedukcja jest specjalnym sposobem myślenia, który pozwala odkryć i udowodnić nowe prawdy za pomocą starych. Dla matematyka powód, dla którego coś jest prawdziwe (zwany dowodem) jest równie ważny jak fakt, że jest to prawda, i ten powód często znajduje się przy użyciu dedukcji. Wykorzystanie dedukcji jest tym, co odróżnia matematykę od innych rodzajów naukowego myślenia, które może opierać się na eksperymentach lub wywiadach.

Logika i rozumowanie są wykorzystywane przez matematyków do tworzenia ogólnych zasad, które są ważną częścią matematyki. Reguły te pomijają informacje, które nie są ważne, dzięki czemu jedna reguła może objąć wiele sytuacji. Znajdując ogólne reguły, matematyka rozwiązuje wiele problemów w tym samym czasie, ponieważ reguły te mogą być wykorzystane do rozwiązywania innych problemów. Reguły te można nazwać twierdzeniami (jeśli zostały udowodnione) lub domysłami (jeśli nie wiadomo, czy są one jeszcze prawdziwe). Większość matematyków stosuje nielogiczne i twórcze rozumowanie w celu znalezienia logicznego dowodu.

Czasami matematyka znajduje i studiuje zasady lub pomysły, których jeszcze nie rozumiemy. Często w matematyce wybiera się pomysły i zasady, ponieważ są one uważane za proste lub schludne. Z drugiej strony, czasami te idee i zasady znajdują się w realnym świecie po tym, jak są studiowane na matematyce; zdarzało się to już wiele razy w przeszłości. Ogólnie rzecz biorąc, studiowanie zasad i idei matematyki może pomóc nam lepiej zrozumieć świat. Niektóre przykłady problemów z matematyką to dodawanie, odejmowanie, mnożenie, dzielenie, rachunek, ułamki i dziesiątki. Problemy z algebrą rozwiązuje się poprzez ocenę pewnych zmiennych. Kalkulator odpowiada na każdy problem matematyczny w czterech podstawowych operacjach arytmetycznych.

Dziedziny nauki matematyki

Numer

Matematyka obejmuje badanie liczb i ilości, jest to dziedzina nauki zajmująca się logiką kształtu, ilości i układu. Większość z wymienionych poniżej dziedzin jest badana w wielu różnych dziedzinach matematyki, w tym w teorii zbiorów i logice matematycznej. Studia nad teorią liczb zazwyczaj koncentrują się bardziej na strukturze i zachowaniu liczb całkowitych niż na rzeczywistych podstawach samych liczb, a więc nie są wymienione w tym podrozdziale.

0 , 1 , 2 , 3 , ... 0,1,2,3 , {\i1}Stypy 0,1,2,3,{\i0} $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\i1,0,1\i0} {\i1}splastyna, -1,0,1,{\i0} $\ldots ,-1,0,1,\ldots$	1 2,2,2,3,0.125,0.125,0.125,0.125,0.125,0.125,0.125. ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\i1}... {\i1}ppi , e, {\i1}sqrt {\i0},{\i1},sldots {\i0} $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\i1+i,2e^{i\pi /3},\i0}, \i0}ldots \i0} $1+i,2e^{i\pi /3},\ldots$
Liczby naturalne	Integratorzy	Racjonalne liczby	Rzeczywiste liczby	Złożone liczby
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\i1}Styl 0,1 , \i0,1 , \i0,\i0,\i0,\i0,\i0,\i0,\i0,\i0,\i0,\i0} $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\i1}... {\i1}...{\i0}, {\i1}...{\i0},{\i1},aldots {\i1} $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\i1}Styl +,-,\i0} $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\i1}splastyna >, \i0}geq , =, \i0}leq , << $>,\geq ,=,\leq ,<$	f ( x ) = x {\i1}styl styropianu f(x)={\i0}sqrt {x}} $f(x)={\sqrt {x}}$
Numery porządkowe	Numery główne	Operacje arytmetyczne	Stosunki arytmetyczne	Funkcje

Struktura

Wiele dziedzin matematyki bada strukturę, jaką posiada dany obiekt. Większość z tych dziedzin jest częścią badań nad algebrą.


Teoria liczb	Algebra abstrakcyjna	Algebra liniowa	Teoria porządku	Teoria grafu

Kształt

Niektóre dziedziny matematyki badają kształty rzeczy. Większość z tych dziedzin jest częścią badań nad geometrią.


Topologia	Geometria	Trigonometria	Geometria różnicowa	Geometria fałdowa

Zmiana

Niektóre dziedziny matematyki badają sposób, w jaki rzeczy się zmieniają. Większość z tych dziedzin jest częścią badań nad analizą.


Calculus	Rachunek wektorowy	Analiza

Równania różnicowe	Systemy dynamiczne	Teoria Chaosu

Matematyka stosowana

Matematyka stosowana wykorzystuje matematykę do rozwiązywania problemów z innych dziedzin, takich jak inżynieria, fizyka i informatyka.

analiza numeryczna - optymalizacja - teoria prawdopodobieństwa - statystyka - finanse matematyczne - teoria gier - fizyka matematyczna - dynamika płynów - algorytmy obliczeniowe

Znane twierdzenia

Te twierdzenia zainteresowały matematyków i ludzi, którzy nie są matematykami.

Twierdzenie Pitagorejczyka - Ostatnie twierdzenie Fermata - Domysł Goldbacha - Twin Prime Conjecture - Twierdzenia Gödela o niekompletności - Domysł Poincarégo - Argument przekątny Kantora - Twierdzenie czterokolorowe - Lemma Zorna - Tożsamość Eulera - Teza o Kościele - Turing

Są to twierdzenia i przypuszczenia, które znacznie zmieniły matematykę.

Hipoteza Riemanna - Hipoteza Continuum - P Versus NP - Twierdzenie Pitagorejczyka - Centralne twierdzenie graniczne - Fundamentalne twierdzenie rachunku - Fundamentalne twierdzenie algebry - Fundamentalne twierdzenie arytmetyczne - Fundamentalne twierdzenie geometrii rzutowej - Twierdzenia klasyfikacyjne powierzchni - Twierdzenie Gaussa-Bonneta - Ostatnie twierdzenie Fermata - Twierdzenie Kantorowicza

Podstawy i metody

Postęp w zrozumieniu natury matematyki wpływa również na sposób, w jaki matematycy badają swój przedmiot.

Filozofia Matematyki - Matematyczny intuicjonizm - Konstruktywizm matematyczny - Podstawy matematyki - Teoria zbiorów - Logika symboliczna - Teoria modelu - Teoria kategorii - Logika - Matematyka odwrotna - Tabela symboli matematycznych

Historia i świat matematyków

Matematyka w historii, a historia matematyki.

Historia matematyki - Oś czasowa matematyki - Matematycy - Medal Fields - Nagroda Abla - Problemy z Nagrodą Millennium (Nagroda Matematyki z Gliny) - Międzynarodowa Unia Matematyczna - Konkursy matematyczne - Myślenie boczne - Matematyka i płeć

Nagrody w dziedzinie matematyki

Nie ma nagrody Nobla w matematyce. Matematycy mogą otrzymać nagrodę Abla i Medal Fieldsa za ważne prace.

Instytut Matematyki Glinianej powiedział, że da milion dolarów każdemu, kto rozwiąże jeden z problemów związanych z Nagrodą Millennium.

Narzędzia matematyczne

Istnieje wiele narzędzi, które są używane do robienia matematyki lub znajdowania odpowiedzi na problemy matematyczne.

Starsze narzędzia

Abacus
Kości Napiera, suwak
Władca i kompas
Obliczenia psychologiczne

Nowsze narzędzia

Kalkulatory i komputery
Języki programowania
Systemy algebry komputerowej (wykaz)
Internetowy skrót i zapis
oprogramowanie do analizy statystycznej (np. SPSS)
Język programowania SAS
Język programowania R

Patrz także

Oś czasowa kobiet w matematyce
Amerykańskie Towarzystwo Matematyczne
Towarzystwo Matematyki Przemysłowej i Stosowanej (Society for Industrial and Applied Mathematics)
Projekt Genealogii Matematycznej
Matematyka Przedmiot Klasyfikacja

Pytania i odpowiedzi

P: Co to jest matematyka?

A: Matematyka to nauka o liczbach, kształtach i wzorach. Słowo to pochodzi od greckiego słowa μάθημα (máthema), które oznacza "naukę, wiedzę lub uczenie się".

P: Jakie są główne dziedziny matematyki?

O: Główne dziedziny matematyki to liczby, struktury (algebra), miejsca (geometria) i zmiany (analiza).

P: Jak matematyka jest wykorzystywana w świecie rzeczywistym?

A: Matematyka stosowana jest przydatna do rozwiązywania problemów w świecie rzeczywistym. Ludzie pracujący w biznesie, nauce, inżynierii i budownictwie korzystają z matematyki.

P: Czy istnieje skrócona wersja słowa "matematyka"?

O: Tak - można go skrócić do "maths" w krajach Brytyjskiej Wspólnoty Narodów lub "math" w Ameryce Północnej.

P: Co oznacza słowo "matematyka"?

O: Słowo "matematyka" pochodzi od greckiego słowa μάθημα (máthema), które oznacza "naukę, wiedzę lub uczenie się".

P: Jakiego rodzaju rozwiązywanie problemów obejmuje matematyka stosowana?

A: Matematyka stosowana polega na rozwiązywaniu rzeczywistych problemów, z którymi stykają się ludzie pracujący w biznesie, nauce, inżynierii i budownictwie.