Funkcja
W matematyce funkcja jest obiektem matematycznym, który po podaniu wejścia wytwarza wyjście - może to być liczba, wektor lub cokolwiek, co może istnieć wewnątrz zbioru rzeczy.
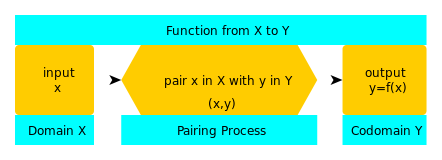
Tak więc funkcja jest jak maszyna, która przyjmuje wartości x i zwraca wyjście y. Zestaw wszystkich wartości, które x może mieć, jest nazywany domeną. Zbiór, który zawiera wszystkie wartości, jakie może mieć y, nazywany jest domeną kodową.
Jeśli tak się stanie, mówimy, że y jest funkcją x, i piszemy y =f(x). f jest nazwą funkcji i piszemy f : X → Y {\i1}stylu f:X\i0}do Y} 
Przykładem funkcji jest f(x)=x+1. Jako wejście podaje się liczbę naturalną x {\i1} 


Metafory
Tabele

Wejścia i wyjścia można umieścić w tabeli jak na rysunku; jest to łatwe, jeśli nie ma zbyt dużej ilości danych.
Wykresy

Na zdjęciu widać, że zarówno 2 jak i 3 zostały sparowane z c; nie jest to dozwolone w drugą stronę, 2 nie mogły wyjść c i d, każde wejście może mieć tylko jedno wyjście. Wszystkie z f ( x ) {\i1}wyświetlacza f(x)} 


Historia
W latach 90-tych XVI wieku GottfriedLeibniz i Johann Bernoulli używali słowa funkcja w literach pomiędzy nimi, więc nowoczesna koncepcja zaczęła się w tym samym czasie co rachunek.
W 1748 roku Leonhard Euler dał: "Funkcja wielkości zmiennej jest wyrażeniem analitycznym, składającym się w jakikolwiek sposób z wielkości zmiennej i liczb lub wielkości stałych", a następnie w 1755 roku: "Jeśli niektóre wielkości tak zależą od innych, że jeśli te ostatnie są zmieniane, to te pierwsze są nazywane funkcjami tych drugich. Definicja ta ma dość szerokie zastosowanie i obejmuje wszystkie sposoby, w jakie jedna wielkość może być określona przez inną. Jeżeli zatem x oznacza wielkość zmienną, to wszystkie wielkości, które w jakikolwiek sposób zależą od x lub są przez niego określane, nazywane są funkcjami x.", co jest bardzo nowoczesne.
Zazwyczaj Dirichletowi przypisuje się wersję używaną w szkołach do drugiej połowy XX wieku: "y jest funkcją zmiennej x, zdefiniowanej w przedziale a < x < b, jeżeli każdej wartości zmiennej x w tym przedziale odpowiada konkretna wartość zmiennej y. Nie ma też znaczenia, w jaki sposób jest ustalana ta zgodność".
W 1939 roku Bourbaki uogólnił definicję Dirichleta i podał jej teoretyczną wersję jako korespondencję pomiędzy wejściami i wyjściami; stosowano ją w szkołach od około 1960 roku.
Wreszcie w 1970 r. Bourbaki podał nowoczesną definicję jako potrójne f = ( X , Y , F ) {\i1}(X,Y,F)} 



Rodzaje funkcji
- Funkcje podstawowe - Funkcje, które są zwykle studiowane w szkole: ułamki, pierwiastki kwadratowe, funkcje sinusoidalne, cosinusoidalne i styczne oraz niektóre inne funkcje.
- Funkcje nie-lementarne - Większość z nich nie korzysta z operacji, których nie uczymy się w szkole (jak + lub -, czy uprawnienia). Wiele funkcji integracyjnych jest nieelementarnych.
- Funkcje odwrotne - Funkcje, które odwracają inną funkcję. Na przykład: jeśli F(x) jest odwrotnością f(x)=y, to F(y)=x. Nie wszystkie funkcje mają inwersje.
- Funkcje specjalne: Funkcje, które mają nazwy. Na przykład: sinusoidalna, cosinusoidalna i styczna. Funkcje takie jak f(x)=3x (trzy razy x) nie są nazywane funkcjami specjalnymi. Mogą one być elementarne, nie elementarne lub odwrotne.
Pytania i odpowiedzi
P: Co to jest funkcja w matematyce?
O: Funkcja w matematyce to obiekt, który po podaniu danych wejściowych daje wynik, którym może być liczba, wektor lub cokolwiek, co może istnieć wewnątrz zbioru rzeczy.
P: Jakie są dwa zbiory związane z funkcjami?
O: Zbiór wszystkich wartości, jakie może mieć x, nazywa się dziedziną, a zbiór zawierający każdą wartość, jaką może mieć y, nazywa się współdziedziną.
P: Jak często oznacza się funkcje?
O: Funkcje często oznacza się kursywą, np. f, g, h.
P: Jak przedstawiamy funkcję?
O: Funkcję przedstawiamy pisząc y = f(x), gdzie f jest nazwą funkcji, a f : X → Y (funkcja z X do Y) przedstawia trzy części funkcji - dziedzinę (X), współdziedzinę (Y) i proces parowania (strzałka).
P: Czy może Pan podać przykład funkcji?
O: Przykładem funkcji jest f(x) = x + 1. Podajemy liczbę naturalną x jako wejście i otrzymujemy liczbę naturalną y, która jest x + 1. Na przykład, podając 3 jako wejście do f, otrzymujemy 4.
P: Czy każda funkcja musi być równaniem?
O: Nie, nie każda funkcja musi być równaniem. Głównym założeniem funkcji jest to, że wejścia i wyjścia są w jakiś sposób łączone - nawet jeżeli jest to bardzo skomplikowane.
Przeszukaj encyklopedię