Całka

W rachunku całka to przestrzeń pod wykresem równania (czasami nazywana "obszarem pod krzywą"). Całka jest przeciwieństwem pochodnej i jest przeciwieństwem rachunku różnicowego. Instrument pochodny jest to stromość (lub "nachylenie"), jako tempo zmian, krzywej. Słowo "całka" może być również użyte jako przymiotnik oznaczający "związane z liczbami całkowitymi".

Symbolem integracji, w rachunku, jest: ∫. {\i1}Stypujący $\int _{\,}^{\,}$ \i0}jak wysoka litera "S". Ten symbol został po raz pierwszy użyty przez Gottfrieda Wilhelma Leibniza, który użył go jako stylizowanego "ſ". (dla sumy, łacina dla sumy) oznacza sumę obszaru objętego równaniem, np. y = f(x).

Całki stałe i pochodne są częścią gałęzi matematyki zwanej rachunkiem. Związek między nimi jest bardzo ważny i nazywany jest fundamentalnym twierdzeniem rachunku. Twierdzenie to mówi, że całka może być odwrócona przez instrument pochodny, podobnie jak dodanie może być odwrócone przez odjęcie.

Integracja pomaga przy próbie rozmnażania jednostek w problemie. Na przykład, jeśli problem z tempem, ( czas dystansu ) {\i1} {\i1}(czas dystansu) {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}poprawnie?{\i0} $\left({\frac {\text{distance}}{\text{time}}}\right)$ Potrzebuje odpowiedzi tylko z dystansem, jednym z rozwiązań jest integracja w odniesieniu do czasu. Oznacza to mnożenie w czasie, aby anulować czas w ( dystans czasowy ) × czas w lewą stronę ((frac \\\u0026apright\u0026apright\u0026apright\u0026apright\u0026apright\u0026apright\u0026apright\u0026apright}) $\left({\frac {\text{distance}}{\text{time}}}\right)\times {\text{time}}$ . Odbywa się to poprzez dodanie do siebie małych fragmentów wykresu stawek. Plastry mają szerokość zbliżoną do zera, ale dodanie ich na zawsze powoduje, że sumują się w całość. Nazywa się to Riemann Sum.

Dodanie tych plasterków razem daje równanie, którego pierwsze równanie jest pochodną. Całościowe są jak sposób na dodanie wielu maleńkich rzeczy razem ręcznie. To jest jak sumowanie, które polega na dodaniu 1 + 2 + 3 + 4.... + n {\i1+2+3+4 ....+n} $1+2+3+4....+n$ . Różnica z integracją polega na tym, że musimy również dodać wszystkie dziesiątki i ułamki pomiędzy nimi.

Innym razem integracja jest pomocna przy znajdowaniu objętości bryły. Może ona dodawać dwuwymiarowe (bez szerokości) plastry bryły razem na zawsze, aż do uzyskania szerokości. Oznacza to, że obiekt ma teraz trzy wymiary: pierwotne dwa i szerokość. To daje objętość opisywanego trójwymiarowego obiektu.

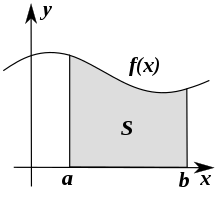
Integracja polega na znalezieniu powierzchni s, przy czym a, b i y = f(x). Wzór na całkę od a do b, wykreślony powyżej, wynosi:
Wzór: ∫ a b f ( x ) d x {\i1}displaystyle \i0}int \i0}limits _{a}^{b}f(x)\i0},dx} $\int \limits _{a}^{b}f(x)\,dx$

Co to jest integralna (animacja)

Metody integracji

Antydydydivative

Zgodnie z podstawowym twierdzeniem rachunku całkowego, integralną częścią jest antyidywatywa.

Jeśli weźmiemy funkcję 2 x {\i0} $2x$ na przykład, i anty-rozróżniający go, możemy powiedzieć, że integralną częścią 2 x {\i0} $2x$ {\i1}jest x 2 {\i1} {\i1} $x^{2}$ . Mówimy o integralności, a nie o integralności, ponieważ antyidywidualna funkcja nie jest wyjątkowa. Na przykład, x 2 + 17 {\i1}styk x^{2}+17}rozróżnia się również do $x^{2}+17$ 2 x {\i1}stylu 2x} $2x$ . Z tego powodu, przy braniu antydyferencyjnej musi być dodana stała C. Nazywa się to nieokreśloną całką. Dzieje się tak dlatego, że znajdując pochodną funkcji, stałe równe 0, jak w funkcji

f ( x ) = 5 x 2 + 9 x + 15 {\i1} styropian f(x)=5x^{2}+9x+15\i0},} $f(x)=5x^{2}+9x+15\,$ .

f ′ ( x ) = 10 x + 9 + 0 {\\i1} $f'(x)=10x+9+0\,$ . Uwaga 0: nie możemy go znaleźć, jeśli mamy tylko pochodną, więc całka jest

∫ ( 10 x + 9 ) d x = 5 x 2 + 9 x + C {\i1}styk stylistyczny \i0}int (10x+9)\i1,dx=5x^{2}+9x+C} $\int (10x+9)\,dx=5x^{2}+9x+C$ .

Równania proste

Proste równanie, takie jak y = x 2 {\i1}wyświetlacz y=x^{2}} $y=x^{2}$ może być zintegrowane w odniesieniu do x przy użyciu następującej techniki. Aby zintegrować, dodajesz 1 do mocy x jest podnoszone do, a następnie dzielisz x przez wartość tej nowej mocy. Dlatego też integracja normalnego równania odbywa się według tej zasady: ∫ x n d x = x n + 1 n + 1 + C {\i1} {\i1}displaystylu \i0}int _{\i1},^{\i0}x^{n}dx={\i1}frac {x^{n+1}}{n+1}+C}. $\int _{\,}^{\,}x^{n}dx={\frac {x^{n+1}}{n+1}}+C$

Styl d $dx$ x {\i1}na końcu jest tym, co pokazuje, że integrujemy się w odniesieniu do x, czyli jak x się zmienia. To może być postrzegane jako odwrotność różnicowania. Jednakże, istnieje stała, C, dodana podczas integracji. Nazywa się to stałą integracji. Jest to wymagane, ponieważ rozróżnienie liczby całkowitej daje w wyniku zero, a więc całkowanie zera (które można umieścić na końcu dowolnej liczby całkowitej) daje liczbę całkowitą, C. Wartość tej liczby całkowitej można znaleźć, korzystając z podanych warunków.

Równania z więcej niż jednym terminem są po prostu zintegrowane poprzez zintegrowanie każdego pojedynczego terminu:

∫ x 2 + 3 x - 2 d x = ∫ x 2 d x + ∫ 3 x d x - ∫ 2 d x = x 3 3 + 3 x 2 - 2 x + C {\i1},}x^{2}+3x-2dx=int _{\i0},}^{\i1}x^{\i0}dx+int _{\i0},}^{\i1}3xdx-int _{\i0},^{\i0}2dx={\i1}{\i1}{\i1}+{\i1}frac {\i1}{\i1}{\i1}{\i1}-2x+C} $\int _{\,}^{\,}x^{2}+3x-2dx=\int _{\,}^{\,}x^{2}dx+\int _{\,}^{\,}3xdx-\int _{\,}^{\,}2dx={\frac {x^{3}}{3}}+{\frac {3x^{2}}{2}}-2x+C$

Integracja obejmująca e i ln

Istnieją pewne zasady integracji przy użyciu e i logarytmu naturalnego. Co najważniejsze, e x {\i1}displaystyle e^{x}} $e^{x}$ jest całką siebie (z dodatkiem stałej integracji): ∫ e x d x = e x + C {\i1}displaystyle \i0}int _{\i1},^{\i0}e^{x}dx=e^{x}+C}. $\int _{\,}^{\,}e^{x}dx=e^{x}+C$

Logarytm naturalny, ln, jest przydatny przy całkowaniu równań z 1 / x {\i1 /x styropianem 1/x} $1/x$ . Nie można ich zintegrować za pomocą powyższego wzoru (dodać jeden do potęgi, podzielić przez potęgę), ponieważ dodanie jednego do potęgi daje 0, a podział przez 0 nie jest możliwy. Zamiast tego, całka 1 / x $1/x$ {\i1}{\i1}jest ln x {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}dx=\i1}{\i1}{\i1}{\i1}l x+C} $\ln x$ $\int _{\,}^{\,}{\frac {1}{x}}dx=\ln x+C$

W bardziej ogólnej formie: ∫ f ′ ( x ) f ( x ) d x = ln | f ( x ) | + C {\i1}displaystyle \i0}int _{\i1},}^{\i1}{\i1}frac {f'(x)}}dx= {\i1}ln {\i1}f(x)|}+C} $\int _{\,}^{\,}{\frac {f'(x)}{f(x)}}dx=\ln {|f(x)|}+C$

Dwa pionowe słupki wskazują wartość bezwzględną; znak (dodatni lub ujemny) f ( x ) f(x) {\i1}jest ignorowany. Dzieje się tak, ponieważ nie ma wartości logarytmu naturalnego liczb ujemnych.

Właściwości

Suma funkcji

Integralna suma funkcji jest sumą wszystkich funkcji, to znaczy,

∫ a b [ f ( x ) + g ( x ) ] d x = ∫ a b f ( x ) d x + ∫ a b g ( x ) d x \\int \limits _{a}^{b}[f(x)+g(x)]\, dx=int \\i0}limits _{a}^{b}f(x)\i0}, dx+int \i0}limits _{a}^{b}g(x)\i0},dx} $\int \limits _{a}^{b}[f(x)+g(x)]\,dx=\int \limits _{a}^{b}f(x)\,dx+\int \limits _{a}^{b}g(x)\,dx$ .

Dowód na to jest prosty: Definicja całki to limit kwot. Tak więc

∫ a b [ f ( x ) + g ( x ) ] d x = lim n → ∞ ∑ i = 1 n ( f ( x i ∗ ) + g ( x i ∗ ) ) {\i1}[f(x)+g(x)]\i0},dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dx=\i0,dxi0,dx $\int \limits _{a}^{b}[f(x)+g(x)]\,dx=\lim _{n\to \infty }\sum _{i=1}^{n}\left(f(x_{i}^{*})+g(x_{i}^{*})\right)$

= lim n → ∞ ∑ i = 1 n f ( x i ∗ ) + ∑ i = 1 n g ( x i ∗ ) {\i0}displaystyle = \i0}lim _{n\i0}do \i0}infty {i=1}^{n}f(x_{i}^{*})+\i0}sum _{i=1}^{n}g(x_{i}^{*))} $=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\sum _{i=1}^{n}g(x_{i}^{*})$

= lim n → ∞ ∑ i = 1 n f ( x i ∗ ) + lim n → ∞ ∑ i = 1 n g ( x i ∗ ) {\i1}displaystyle = ślim _{n\i0} {\i1}sum _{i=1}^{n}f(x_{i}^{*})+ ślim _{n\i1}{\i1}^{\i1}g(x_{i}^{*))} $=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\lim _{n\to \infty }\sum _{i=1}^{n}g(x_{i}^{*})$

= ∫ a b f ( x ) d x + ∫ a b g ( x ) d x {\i0}displaystyle =int \i0}limits _{a}^{b}f(x)\i0},dx+int \i0}limits _{a}^{b}g(x)\i0},dx} $=\int \limits _{a}^{b}f(x)\,dx+\int \limits _{a}^{b}g(x)\,dx$

Należy pamiętać, że obie całki mają te same granice.

Stałe w integracji

Gdy stała znajduje się w integralnej części funkcji, można ją wyjąć. Ponadto, gdy stałej c nie towarzyszy funkcja, jej wartością jest c * x. To znaczy,

∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x {\i1}displaystyle \i0}int \i0}limits _{a}^{b}cf(x)\i0},dx=c\i0}int \i0}limits _{a}^{b}f(x)\i0},dx} $\int \limits _{a}^{b}cf(x)\,dx=c\int \limits _{a}^{b}f(x)\,dx$ oraz

Można to zrobić tylko przy pomocy stałej.

∫ a b c d x = c ( b - a ) {\i1}displaystyle \i0}int \i0}limits _{a}^{b}c\i0},dx=c(b-a)} $\int \limits _{a}^{b}c\,dx=c(b-a)$

Dowodem jest ponownie definicja integralności.

Inne

Jeżeli a, b i c są w porządku (tzn. po sobie na osi x), całka f(x) z punktu a do punktu b plus całka f(x) z punktu b do c jest równa całce z punktu a do c. To znaczy,

∫ a b f ( x ) d x + ∫ b c f ( x ) d x = ∫ a c f ( x ) d x {\i1}displaystyle \i0}int \i0}f(x)\i0},dx+int \i0}f(x)\i0},dx=int \i0}f(x)\i0}f(x)\i0}, $\int \limits _{a}^{b}f(x)\,dx+\int \limits _{b}^{c}f(x)\,dx=\int \limits _{a}^{c}f(x)\,dx$ dx}jeśli są w porządku. (To również ma miejsce, gdy a, b, c nie są w porządku, jeżeli zdefiniujemy ∫ a b f ( x ) d x = - ∫ b a f ( x ) d x {\i1}displaystyle \i0}int \i0}f(x)\i0},dx=-int \i0}limits _{b}^{a}f(x)\i0},dx} $\int \limits _{a}^{b}f(x)\,dx=-\int \limits _{b}^{a}f(x)\,dx$ .)

∫ a f ( x ) d x = 0 {\i1}splaystyle \i0}int \i0}limits _{a}^{a}f(x)\i0} $\int \limits _{a}^{a}f(x)\,dx=0$ . To wynika z podstawowego twierdzenia rachunku (FTC): F(a)-F(a)=0

∫ a b f ( x ) d x = - ∫ b a f ( x ) d x {\i1}displaystyle \i0}int \i0}f(x)\i0},dx=-int \i0}limits _{b}^{a}f(x)\i0},dx} $\int \limits _{a}^{b}f(x)\,dx=-\int \limits _{b}^{a}f(x)\,dx$ Znowu, po FTC: F ( b ) - F ( a ) = - [ F ( a ) - F ( b ) ] {\i1}-[F(b)-F(a)=-[F(a)-F(b)]} $F(b)-F(a)=-[F(a)-F(b)]$

Pytania i odpowiedzi

P: Co to jest całka?

O: Całka to przestrzeń pod wykresem równania, zwana również "obszarem pod krzywą". Jest to odwrotność pochodnej i część gałęzi matematyki zwanej rachunkiem.

P: Jak wygląda symbol całki?

P: Jak całki są powiązane z pochodnymi?

O: Całki i pochodne łączy podstawowe twierdzenie rachunku, które mówi, że całkę można odwrócić przez pochodną, podobnie jak dodawanie można odwrócić przez odejmowanie.

P: Kiedy można stosować całkowanie?

O: Całkowanie można stosować przy mnożeniu jednostek w zadaniu lub przy określaniu objętości bryły. Pomaga dodawać do siebie dwuwymiarowe kawałki, aż do uzyskania szerokości, co daje obiektowi trzy wymiary i jego objętość.

P: W jaki sposób całkowanie jest podobne do sumowania?

O: Całkowanie jest podobne do sumowania w tym sensie, że dodaje wiele drobnych rzeczy do siebie, ale w przypadku całkowania musimy dodać również wszystkie części dziesiętne i ułamki.

P: Co oznacza suma Riemanna?

O: Suma Riemanna oznacza dodawanie do siebie małych fragmentów wykresu tempa, aż zsumują się w jedno całe równanie.