Mnożenie
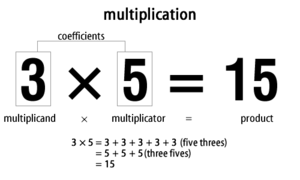
Mnożenie to operacja arytmetyczna polegająca na znalezieniu iloczynu dwóch liczb. Mnożenie jest trzecią operacją w matematyce po dodaniu, która jest pierwszą, odejmowanie, które jest drugą, a następnie jest mnożenie.
W przypadku liczb naturalnych, mówi ona o liczbie płytek w prostokącie, gdzie jedna z dwóch liczb jest równa liczbie płytek z jednej strony, a druga liczba jest równa liczbie płytek z drugiej strony.
W przypadku liczb rzeczywistych, mówi ona o obszarze prostokąta, gdzie pierwsza liczba jest równa wielkości jednego boku, a druga - wielkości drugiego boku.
Na przykład, trzy pomnożone przez pięć to suma pięciu trójek dodanych do siebie, lub suma trzech piątek. Można to zapisać jako 3 × 5 = 15, lub powiedzieć, że "trzy razy pięć równa się piętnaście". Matematycy nazywają te dwie liczby, które chcemy pomnożyć razem "współczynniki", albo "mnożniki" i "mnożniki" oddzielnie. Multiplikant × mnożnik = iloczyn.
Mnożenie liczb jest uważane za komutatywne - gdy kolejność liczb nie ma wpływu na wartość produktu. Dotyczy to liczb całkowitych (całych), np. 4 × 6 jest takie same jak 6 × 4, a także liczb racjonalnych (ułamkowych) oraz wszystkich innych liczb rzeczywistych (reprezentowanych jako pole w linii ciągłej), a także liczb złożonych (reprezentowanych jako pole w płaszczyźnie). Nie jest to prawdą w przypadku liczb kwaternionowych (liczb reprezentowanych jako pierścień w przestrzeni czterowymiarowej), wektorów lub macierzy.
Definicja zwielokrotnienia jako wielokrotnego dodawania zapewnia sposób na osiągnięcie zbioru teoretycznych interpretacji zwielokrotnienia liczb kardynalnych. Dokładniejszą reprezentacją jest myślenie o tym jako o skalowaniu liczb. Ta animacja pokazuje, że 3 są mnożone przez 2, dając w rezultacie 6. Zauważ, że niebieska kropka na niebieskim odcinku o długości 3 jest umieszczona na pozycji 1, a niebieski odcinek jest skalowany tak, że ta kropka jest umieszczona na końcu czerwonego odcinka o długości 2. Przy mnożeniu przez dowolny X, niebieska kropka zawsze zaczyna się od 1 i kończy na X. Działa to nawet dla X mniejszych niż 1, lub ujemnych.
Przeciwieństwem mnożenia jest podział.
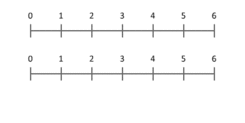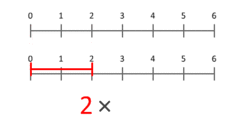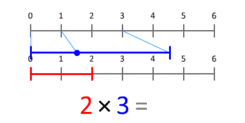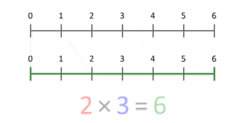
Tabela mnożenia
Nauczyciele zazwyczaj wymagają od swoich uczniów zapamiętania tabeli pierwszych 9 liczb podczas nauczania mnożenia.
| Tabela nr 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabela mnożenia | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Powiązane strony
- Dodatek
- Numer kwadratowy
- Odejmowanie
Pytania i odpowiedzi
P: Co to jest mnożenie?
A: Mnożenie to operacja arytmetyczna służąca do znajdowania iloczynu dwóch liczb w matematyce. Często przedstawia się ją za pomocą symboli takich jak × i ⋅.
P: Jak nazywa się dwie liczby, które należy pomnożyć?
O: Dwie liczby do pomnożenia nazywane są "współczynnikami" lub osobno "mnożnikiem" i "mnożnikiem".
P: Czy mnożenie jest komutatywne?
O: Tak, o mnożeniu liczb mówi się, że jest komutatywne - gdy kolejność liczb nie wpływa na wartość iloczynu. Jest to prawdą dla liczb całkowitych, racjonalnych, rzeczywistych i złożonych. Nie jest to jednak prawdą dla kwaternionów, wektorów i macierzy.
P: Jak można interpretować mnożenie liczb kardynalnych?
O: Mnożenie liczb kardynalnych możemy interpretować jako skalowanie wielkości - gdy jedna liczba (mnożnik) jest skalowana tak, że kropka umieszczona w pozycji 1 kończy się w pewnym punkcie (mnożniku).
P: Jak przedstawić trzy pomnożone przez pięć?
O: Trzy pomnożone przez pięć można zapisać jako 3 × 5 = 15, lub powiedzieć "trzy razy pięć równa się piętnaście".
P: Co jest przeciwieństwem mnożenia?
O: Przeciwieństwem mnożenia jest dzielenie.
