Wektor

Przykłady wektorów

• Jan idzie na północ 20 metrów. Kierunek "północ" wraz z odległością "20 metrów" jest wektorem.
• Jabłko spada w dół z prędkością 10 metrów na sekundę. Kierunek "w dół" w połączeniu z prędkością "10 metrów na sekundę" to wektor. Ten rodzaj wektora jest również nazywany prędkością.

Przykłady skalarów

• Odległość między dwoma miejscami jest równa 10 kilometrów. Ta odległość nie jest wektorem, ponieważ nie zawiera kierunku.
• Liczba owoców w skrzynce nie jest wektorem.
• Osoba wskazująca nie jest wektorem, ponieważ jest tylko kierunek. Nie ma wielkości (odległości od palca osoby do budynku, na przykład).
• Długość obiektu.
• Samochód jedzie z prędkością 100 kilometrów na godzinę. To nie jest opis wektora, ponieważ jest tylko wielkość, ale nie ma kierunku.

Więcej przykładów wektorów

• Przemieszczenie jest wektorem. Przemieszczenie to odległość, o jaką coś porusza się w określonym kierunku. Sama miara odległości jest skalarem.
• Siła, która zawiera kierunek jest wektorem.
• Prędkość jest wektorem, ponieważ jest to prędkość w określonym kierunku.
• Przyspieszenie to szybkość zmiany prędkości. Obiekt przyspiesza, jeśli zmienia prędkość lub zmienia kierunek.

Jak dodać wektory

Dodawanie wektorów na papierze metodą "z głową do ogona

Metoda dodawania wektorów od głowy do ogona jest przydatna do oszacowania na papierze wyniku dodawania dwóch wektorów. Aby to zrobić:

• Każdy wektor jest narysowany jako strzałka z ilością długości za nią, gdzie każda jednostka długości na papierze reprezentuje pewną wielkość wektora.
• Narysuj następny wektor, z ogonem (końcem) drugiego wektora na czole (przodzie) pierwszego wektora.
• Powtórz czynność dla wszystkich kolejnych wektorów: Narysuj ogon kolejnego wektora na wysokości głowy poprzedniego.
• Narysuj linię od ogona pierwszego wektora do głowy ostatniego wektora - to jest wypadkowa (suma) wszystkich wektorów.

Nazywa się to metodą "Head to Tail", ponieważ każda głowa z poprzedniego wektora prowadzi do ogona następnego.

Używanie formularza komponentu

^{[wymaga wyjaśnienia]}

Użycie formy składowej do dodania dwóch wektorów dosłownie oznacza dodanie składowych wektorów, aby utworzyć nowy wektor. Na przykład, niech a i b będą dwoma dwuwymiarowymi wektorami. Wektory te można zapisać w postaci ich składowych.

a = ( a x , a y ) { {displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) { {displaystyle ™mathbf {b} =(b_{x},b_{y})}

Załóżmy, że c jest sumą tych dwóch wektorów, więc c = a + b. Oznacza to, że c = ( a x + b x , a y + b y ) { {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Oto przykład dodawania dwóch wektorów, używając ich form składowych.

a = ( 3 , - 1 ) {displaystyle ™mathbf {a} =(3,-1)}

b = ( 2 , 2 ) { {displaystyle \mathbf {b} =(2,2)}

c = a + b { {{displaystyle \mathbf {c} = \mathbf {a} + \mathbf {b} }

= ( a x + b x , a y + b y ) { {displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}

= ( 3 + 2 , - 1 + 2 ) {displaystyle =(3+2,-1+2)}

= ( 5 , 1 ) {displaystyle =(5,1)}

Ta metoda działa dla wszystkich wektorów, nie tylko dwuwymiarowych.

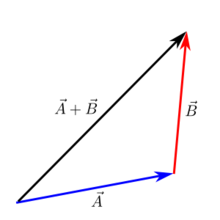
Dodatki za głowę z ogonem

Jak mnożyć wektory

Używając iloczynu kropkowego

Iloczyn kropkowy jest jedną z metod mnożenia wektorów. Jego wynikiem jest skalar. Używa formy składowej:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {{displaystyle {{begin{aligned}} \mathbf {a} =(2,3)\mathbf {b} =(1,4)\mathbf {a} =(2,3)\mathbf {b} =(2,3)\mathbf {b} =(1,4)\mathbf {b} =(2\cdot 1)+(3\cdot 4)\=2+12=14\end{aligned}}

Wykorzystanie iloczynu krzyżowego

Iloczyn krzyżowy to kolejna metoda mnożenia wektorów. Daje on kolejny wektor. Używając formy składowej:

a × b = | a | b | sin ( θ ) n { {displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} =|mathbf {a} =|mathbf {b} |sin(\theta )\mathbf {n} }

Tutaj | a | {displaystyle |mathbf {a} |} oznacza długość a {{displaystyle \mathbf {a}}, a n {{displaystyle \mathbf {n}} }, a n {displaystyle \mathbf {n} } jest wektorem jednostkowym prostopadłym zarówno do a {displaystyle ™mathbf {a} } jak i b {displaystyle ™mathbf {a} }. } i b {displaystyle \mathbf {b} } .

Mnożenie przez skalar

Aby pomnożyć wektor przez skalar (zwykłą liczbę), mnożysz tę liczbę przez każdy składnik wektora:

c x = ( c x 1 , c x 2 , . . . , c x n ) { {cx} =(c x_{1},c x_{2},...,c x_{n})}

Przykładem tego jest

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) { {displaystyle {{begin{aligned}}c=5{mathbf {x} =(3,4)}}, {{mathbf {x} =(5{cdot 3,5{cdot 4}} =(15,20)}} end{aligned}}

Powiązane strony

• Grafika wektorowa
• Pole wektorowe