Różniczka funkcji

Rachunek różniczkowy, gałąź rachunku, jest procesem znajdowania tempa zmian zmiennej w stosunku do innej zmiennej, przy użyciu funkcji. Jest to sposób, aby dowiedzieć się, jak zmienia się kształt od jednego punktu do drugiego, bez konieczności dzielenia kształtu na nieskończoną liczbę części. Rachunek różniczkowy jest przeciwieństwem rachunku całkowego. Został on opracowany w latach 70. i 80. XVI wieku przez Sir Isaaca Newtona i Gottfrieda Leibniza.

Tło

W przeciwieństwie do liczby takiej jak 5 lub 200, zmienna może zmieniać swoją wartość. Na przykład, odległość i czas są zmiennymi. Podczas olimpijskiego wyścigu biegowego, gdy osoba biegnie, jej odległość od linii startu rośnie. W tym samym czasie stoper lub zegar mierzy czas. Możemy zmierzyć średnią prędkość biegacza, jeśli podzielimy odległość, którą przebył, przez czas, który mu to zajęło. Ale to nie mówi, z jaką prędkością biegła dana osoba dokładnie w 1,5 sekundy wyścigu. Gdybyśmy mieli dystans w 1 sekundzie i dystans w 2 sekundach, nadal mielibyśmy tylko średnią, choć prawdopodobnie byłaby ona bardziej poprawna niż średnia dla całego wyścigu.

Dopóki nie wynaleziono rachunku, jedynym sposobem, by to obliczyć, było pocięcie czasu na coraz mniejsze kawałki, tak by średnia prędkość w tym czasie była coraz bliższa rzeczywistej prędkości dokładnie 1,5 sekundy. Był to bardzo długi i trudny proces i musiał być wykonywany za każdym razem, gdy ludzie chcieli coś wymyślić. Wyobraź sobie kierowcę, który próbuje określić prędkość samochodu, używając tylko jego licznika kilometrów i zegara, bez prędkościomierza!

Bardzo podobnym problemem jest znalezienie nachylenia (jak stroma jest linia) w dowolnym punkcie krzywej. Nachylenie linii prostej jest łatwe do obliczenia - jest to po prostu stosunek wysokości (y lub pionu) do szerokości (x lub poziomu). Jeśli prosta jest równoległa do osi x, to jej nachylenie wynosi zero. Jeśli linia prosta przechodzi przez (x,y) = (2,10) i (4,18), to linia wznosi się o 8 i przechodzi przez 2, więc jej nachylenie wynosi 8 podzielone przez 2, czyli 4.

Na "krzywej" jednak, nachylenie jest zmienne (ma różne wartości w różnych punktach), ponieważ linia zakręca. Ale jeśli krzywa zostałaby pocięta na bardzo, bardzo małe kawałki, krzywa w punkcie wyglądałaby prawie jak bardzo krótka linia prosta. Aby obliczyć jej nachylenie, można więc narysować linię prostą przechodzącą przez punkt o takim samym nachyleniu jak krzywa w tym punkcie. Jeśli zrobimy to dokładnie tak, jak należy, prosta będzie miała takie samo nachylenie jak krzywa i nazywana jest styczną. Ale nie ma sposobu, aby wiedzieć (bez rachunku), czy tangens jest dokładnie w prawo, a nasze oczy nie są wystarczająco dokładne, aby być pewnym, czy jest to dokładne lub po prostu bardzo blisko.

Newton i Leibniz znaleźli sposób na dokładne obliczenie nachylenia (lub prędkości w przykładzie z odległością) za pomocą prostych i logicznych reguł. Podzielili oni krzywą na nieskończoną liczbę bardzo małych kawałków. Następnie wybrali punkty po obu stronach interesującego ich punktu i wyznaczyli styczne w każdym z nich. W miarę zbliżania się punktów do interesującego ich punktu, nachylenie krzywej zbliżało się do pewnej wartości, ponieważ styczne zbliżały się do rzeczywistego nachylenia krzywej. Stwierdzili, że ta szczególna wartość, do której się zbliża, jest rzeczywistym nachyleniem.

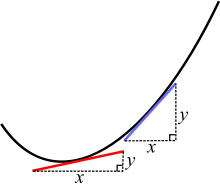
Na krzywej, dwa różne punkty mają różne nachylenia. Czerwona i niebieska linia są styczne do krzywej.

Jak to działa?

Powiedzmy, że mamy funkcję y = f(x). f to skrót od function, więc to równanie oznacza, że "y jest funkcją x". To mówi nam, że to, jak wysoko y jest na osi pionowej, zależy od tego, jakie jest x (oś pozioma) w tym czasie. Na przykład, z równaniem y = x², wiemy, że jeśli x wynosi 1, to y będzie równe 1; jeśli x wynosi 3, to y będzie równe 9; jeśli x wynosi 20, to y będzie równe 400.

Wybierz punkt A na krzywej i nazwij jego położenie poziome x. Następnie wybierz inny punkt B na krzywej, który jest trochę dalej w poprzek niż A i nazwij jego położenie poziome x + h. Nie ma znaczenia ile wynosi h, jest to bardzo mała liczba.

Więc kiedy przechodzimy z punktu A do punktu B, położenie pionowe zmieniło się z f(x) na f(x + h), a położenie poziome z x na x + h. Teraz pamiętaj, że nachylenie to stosunek długości drogi w górę do długości drogi w poprzek. Zatem nachylenie będzie wynosić:

f ( x + h ) - f ( x ) h { {frac {f(x+h)-f(x)}{h}}. ${\frac {f(x+h)-f(x)}{h}}$

Jeśli przybliżymy B do A - co oznacza, że h staje się coraz bliższe 0 - to będziemy mogli wiedzieć, jakie jest nachylenie w punkcie A.

lim h → 0 f ( x + h ) - f ( x ) h {{displaystyle }} lim _{h → 0}{{frac {f(x+h)-f(x)}{h}}. $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Wróćmy teraz do y = x². Nachylenie tej prostej można wyznaczyć w następujący sposób:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {{displaystyle {{begin{aligned}&}=lim _{hrightarrow 0}{}{frac {f(x+h)-f(x)}{h}}}. ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Stosując twierdzenie dwumianowe, które mówi, że ( x + y ) 2 = x 2 + 2 x y + y 2 {(x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ możemy sprowadzić do:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {displaystyle {{begin{aligned}}&==lim _{hrightarrow 0}{}{hrac {x^{2}+2xh+h^{2}-x^{2}}{h}}}}&=lim _{hrightarrow 0}{hrac {2xh+h^{2}}{h}}}}. ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Wiemy więc bez konieczności rysowania linii stycznych, że w każdym punkcie krzywej f(x) = x², pochodna f'(x) (oznaczona apostrofem) będzie równa 2x w każdym punkcie. Ten proces obliczania nachylenia przy użyciu granic nazywamy różniczkowaniem lub znajdowaniem pochodnej.

Leibniz doszedł do tego samego wyniku, ale nazwał h "dx", co oznacza "maleńką ilość x". Wynikającą z tego zmianę w f(x) nazwał "dy", co oznacza "maleńką ilość y". Notacja Leibniza jest używana w większej liczbie książek, ponieważ jest łatwa do zrozumienia, gdy równania stają się bardziej skomplikowane. W notacji Leibniza:

d y d x = f ′ ( x ) {frac {dy}{dx}}=f'(x)}. ${\frac {dy}{dx}}=f'(x)$

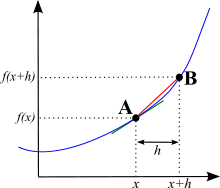
Rysunek pokazujący, co oznaczają x i x + h na krzywej.

Zasady

Używając powyższego systemu, matematycy opracowali reguły, które działają cały czas, niezależnie od tego, na jaką funkcję patrzymy. (Uwaga: tutaj, u {displaystyle u} $u$ i v {displaystyle v} $v$ są funkcjami x {displaystyle x}).

Stan	Funkcja	Pochodna	Przykład	Pochodna
Liczba sama w sobie	y = a {{displaystyle y=a} $y=a$	d y d x = 0 {displaystyle {frac {dy}{dx}}=0}. ${\frac {dy}{dx}}=0$	y = 3 {{displaystyle y=3}} $y=3$	0 {{displaystyle 0}} $0$
Linia prosta	y = m x + c {{displaystyle y=mx+c}} $y=mx+c$	d y d x = m {displaystyle {frac {dy}{dx}}=m}. ${\frac {dy}{dx}}=m$	y = 3 x + 5 {{displaystyle y=3x+5}} $y=3x+5$	3 {styl wyświetlania 3} $3$
x do potęgi liczby	x a {{displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {{displaystyle {{frac {dy}{dx}}=ax^{a-1}}. ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {displaystyle x^{12}} $x^{12}$	12 x 11 {{displaystyle 12x^{11}} $12x^{11}$
Liczba pomnożona przez funkcję	y = c ⋅ u {{displaystyle y=cdot u} $y=c\cdot u$	d y d x = c d u d x {{displaystyle {{frac {dy}{dx}}=c{{{frac {du}{dx}}}}. ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {przykład 3(2x+1)} $3(2x+1)$
Funkcja plus inna funkcja	y = u + v {{displaystyle y=u+v}} $y=u+v$	d y d x = d u d x + d v d x {{displaystyle {{{frac {dy}{dx}}}={{{frac {du}{dx}}+{{{frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {{displaystyle y=3x^{2}+{sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 x {{displaystyle 6x+{frac {1}{sqrt {x}}}} $6x+{\frac {1}{\sqrt {x}}}$
Funkcja minus inna funkcja	y = u - v {{displaystyle y=u-v}} $y=u-v$	d y d x = d u d x - d v d x {{displaystyle {{{frac {dy}{dx}}}={{{frac {du}{dx}}-{{{frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {{displaystyle y=3x^{2}-{sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 x {{displaystyle 6x-{frac {1}{sqrt {x}}}} $6x-{\frac {1}{\sqrt {x}}}$
Reguła iloczynuFunkcja pomnożona przez inną funkcję	y = u ⋅ v {displaystyle y=u v} $y=u\cdot v$	d y d x = d u d x v + u d v d x { {displaystyle {{{frac {dy}{dx}}}={{{frac {du}{dx}}v+u{{{frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) { {displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) { (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Reguła ilorazuFunkcja podzielna przez inną funkcję	y = u v {{displaystyle y={frac {u}{v}}}. $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {{displaystyle}}={{{displayfrac {du}{dx}}v-u{{displayfrac {dv}{dx}}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {{displaystyle y={frac {x^{2}+2}{x-1}}}. $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Reguła łańcuchowaUżywana dla funkcji złożonych	y = u ∘ v {displaystyle y=u v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {{displaystyle {{frac {dy}{dx}}={{{frac {dy}{du}}}}}. ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {{displaystyle y={sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 x - 1 = 1 2 x - 1 { {frac {2}{2x-1}}}}={frac {1}{sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Funkcja wykładnicza	y = e x {{displaystyle {{frac {}{}}y=e^{x}}. ${\frac {}{}}y=e^{x}$	d y d x = e x {displaystyle {frac {dy}{dx}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {{displaystyle {{frac {}{}}y=e^{x}}. ${\frac {}{}}y=e^{x}$	e x {{displaystyle {{frac {{}}e^{x}} ${\frac {}{}}e^{x}$

Pytania i odpowiedzi

P: Co to jest rachunek różniczkowy?

O: Rachunek różniczkowy to dziedzina rachunku, która bada tempo zmian jednej zmiennej w stosunku do innej zmiennej za pomocą funkcji.

P: Jak to działa?

O: Rachunek różniczkowy pozwala stwierdzić, jak zmienia się kształt od jednego punktu do drugiego, bez konieczności dzielenia kształtu na nieskończoną liczbę części.

P: Kto opracował rachunek różniczkowy?

O: Rachunek różniczkowy został opracowany w latach 70-tych i 80-tych XVI wieku przez Sir Isaaca Newtona i Gottfrieda Leibniza.

P: Co to jest rachunek całkowy?

O: Rachunek całkowy jest przeciwieństwem rachunku różniczkowego. Służy do wyznaczania powierzchni pod krzywymi i objętości brył o zakrzywionych powierzchniach.

P: Kiedy powstał rachunek różniczkowy?

O: Rachunek różniczkowy został opracowany w latach 70-tych i 80-tych XVI wieku przez Sir Isaaca Newtona i Gottfrieda Leibniza.

P: Jakie są niektóre zastosowania rachunku różniczkowego?

O: Niektóre zastosowania rachunku różniczkowego to obliczanie prędkości, przyspieszenia, wartości maksymalnych lub minimalnych, problemy optymalizacyjne, pola nachylenia itp.

P: Dlaczego stosujemy rachunek różniczkowy zamiast dzielenia kształtów na nieskończoną liczbę części?

O: Stosujemy rachunek różniczkowy, ponieważ dzięki niemu możemy dowiedzieć się, jak zmienia się kształt od jednego punktu do drugiego, bez konieczności dzielenia kształtu na nieskończoną liczbę części.