Funkcja wykładnicza
W matematyce funkcja wykładnicza to funkcja, która szybko rośnie. Dokładniej, jest to funkcja exp ( x ) = e x {displaystyle \exp(x)=e^{x}} 
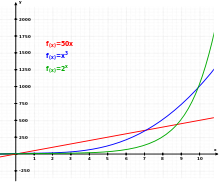
Trzy różne funkcje: Linear (czerwona), Cubic (niebieska) i Exponential (zielona).
Właściwości
Ponieważ funkcje wykładnicze używają wykładania, postępują zgodnie z tymi samymi zasadami. Tak więc,
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {{displaystyle \a_exp(x+y)=e^{x+y}}. 

Logarytm naturalny jest operacją odwrotną do funkcji wykładniczej.
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {{displaystyle ln(x)= log _{e}(x)={frac {log(x)}{log(e)}}
Funkcja wykładnicza spełnia ciekawą i ważną własność w rachunku różniczkowym,
d d x e x = e x {{displaystyle {{frac {{mathrm {d}} {{mathrm {d} x}}e^{x}=e^{x}} 
Oznacza to, że nachylenie funkcji wykładniczej jest samą funkcją wykładniczą, a następnie oznacza to, że ma ona nachylenie równe 1 przy x = 0 {przy x=0}
Aplikacje
Funkcja wykładnicza jest jedną z najbardziej użytecznych funkcji matematycznych. Jest używana do przedstawiania wzrostu wykładniczego, który ma zastosowanie praktycznie we wszystkich przedmiotach ścisłych, a także jest popularny w finansach. Zdarza się również rozkład wykładniczy, na przykład rozpad promieniotwórczy i absorpcja światła.
Jednym z przykładów funkcji wykładniczej w prawdziwym życiu mogą być odsetki w banku. Jeśli dana osoba wpłaci 100 funtów na konto, które jest oprocentowane na 3% miesięcznie, to saldo każdego miesiąca będzie wynosiło (zakładając, że pieniądze są nietknięte):
| Miesiąc | Saldo | Miesiąc | Saldo |
| Styczeń | £100.00 | Lipiec | £119.41 |
| Luty | £103.00 | Sierpień | £122.99 |
| Marzec | £106.09 | Wrzesień | £126.68 |
| Kwiecień | £109.27 | Październik | £130.48 |
| Maj | £112.55 | Listopad | £134.39 |
| Czerwiec | £115.93 | Grudzień | £138.42 |
Zauważ, jak dodatkowe pieniądze z odsetek rosną każdego miesiąca. Im większe jest saldo początkowe, tym więcej odsetek otrzyma dana osoba.
Poniżej przedstawiono dwa przykłady matematyczne funkcji wykładniczych.
| a=2
| a=3
|
Związek ze stałą matematyczną e
Mimo że podstawą ( a}
Liczba e jest ważna dla każdej funkcji wykładniczej. Na przykład, bank codziennie wypłaca odsetki w wysokości 0,01 procent. Pewna osoba bierze swoje pieniądze z odsetek i wkłada je do pudełka. Po 10 000 dniach (około 30 latach) ma 2 razy więcej pieniędzy niż na początku. Inna osoba bierze swoje pieniądze z odsetek i wkłada je z powrotem do banku. Ponieważ bank płaci mu teraz odsetki od jego odsetek, ilość pieniędzy jest funkcją wykładniczą. Po 10 000 dniach nie ma on 2 razy więcej pieniędzy, niż miał na początku, ale ma 2,718145 razy więcej pieniędzy, niż miał na początku. Liczba ta jest bardzo bliska liczbie e. Jeśli bank będzie płacił odsetki częściej, więc kwota płacona za każdym razem będzie mniejsza, to liczba ta będzie bliższa liczbie e.
Można również spojrzeć na rysunek, aby zobaczyć, dlaczego liczba e jest ważna dla funkcji wykładniczych. Na rysunku znajdują się trzy różne krzywe. Krzywa z czarnymi punktami to funkcja wykładnicza o podstawie trochę mniejszej niż e. Krzywa z krótkimi czarnymi liniami to funkcja wykładnicza o podstawie trochę większej niż e. Niebieska krzywa to funkcja wykładnicza o podstawie dokładnie równej e. Czerwona linia jest styczna do niebieskiej krzywej. Styka się ona z krzywą niebieską w jednym punkcie, nie przecinając jej. Osoba może zobaczyć, że czerwona krzywa przecina oś x, linię biegnącą od lewej do prawej, w punkcie -1. Jest to prawdą tylko dla niebieskiej krzywej. To jest powód, dla którego funkcja wykładnicza o podstawie e jest szczególna.
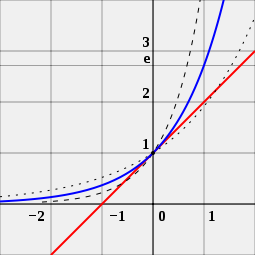
e jest jedyną taką liczbą a, że wartość pochodnej funkcji wykładniczej f (x) = ax (krzywa niebieska) w punkcie x = 0 wynosi dokładnie 1. Dla porównania pokazane są funkcje 2x (krzywa kropkowana) i 4x (krzywa przerywana), które nie są styczne do prostej o nachyleniu 1 (czerwona).
Pytania i odpowiedzi
P: Co to jest funkcja wykładnicza?
O: Funkcja wykładnicza to funkcja matematyczna, która rośnie coraz szybciej.
P: Jak funkcja wykładnicza wyraża się matematycznie?
A: Funkcja wykładnicza wyraża się matematycznie jako exp(x) = e^x, gdzie e jest stałą Eulera.
P: Co oznacza stała Eulera?
O: Stała Eulera jest liczbą irracjonalną, która w przybliżeniu wynosi 2,71828.
P: Czy funkcja wykładnicza jest zawsze rosnąca?
O: Tak, funkcja wykładnicza zawsze zwiększa swoją wartość wraz ze wzrostem x.
P: Czy istnieje granica, jak szybko może rosnąć funkcja wykładnicza?
O: Nie, nie ma ograniczenia co do szybkości wzrostu funkcji wykładniczej, ponieważ przy większych wartościach x nadal rośnie.
P: Jak można obliczyć stałą Eulera?
O: Stałą Eulera można obliczyć za pomocą metod numerycznych, takich jak szereg Taylora lub ułamki ciągłe.
P: Jakie są inne zastosowania funkcji wykładniczej poza matematyką?
O: Funkcje wykładnicze mają wiele zastosowań poza matematyką, w tym w fizyce, chemii, biologii, ekonomii i inżynierii.
Przeszukaj encyklopedię

