Zbiór

Notacja

Większość matematyków używa wielkich, kursywnych (zwykle rzymskich) liter do pisania o zbiorach. Rzeczy, które są postrzegane jako elementy zbiorów są zwykle pisane małymi literami rzymskimi.

Jednym ze sposobów przedstawienia zbioru jest lista jego członków, oddzielonych przecinkami i ujętych w nawiasy klamrowe. Na przykład,

• X={1,2,3} jest zbiorem, który ma elementy 1, 2, i 3.

Innym sposobem jest stwierdzenie, co jest prawdą o członkach zbioru, na przykład w ten sposób:

• {x | x jest liczbą naturalną & x < 4}.

W języku angielskim mówionym jest to: "zbiór wszystkich x takich, że x jest liczbą naturalną i x jest mniejsze niż cztery".

Pusty zbiór jest zapisywany w specjalny sposób:

• ∅ { {displaystyle \emptyset }

Gdy obiekt a jest członkiem zbioru A, zapisuje się to jako:

• a ∈ A.

W mówionym angielskim, to jest: "a is a member of A"

Co zrobić z zestawami

Element

Do worka można włożyć różne rzeczy. Później ważnym pytaniem będzie, czy pewna rzecz jest w tym worku. Matematycy nazywają to elementem zbioru. Coś jest elementem zbioru, jeśli ta rzecz może być znaleziona w danym worku. Symbolem używanym do tego jest ∈ {displaystyle ∈ }

a ∈ A {{displaystyle a} } }

oznacza, że a {styl a} znajduje się w worku A {styl a} jest w worku A {mathbf {A} }

Pusty zbiór

Podobnie jak worek, zbiór może być pusty. Pusty zestaw jest jak pusta torba: nie ma w nim żadnych rzeczy.

Porównywanie zestawów

Można porównać dwa zestawy. To jest jak patrzenie na dwie różne torby. Jeśli zawierają one te same rzeczy, są równe.

Cardinality of a set

Kiedy matematycy mówią o zbiorze, czasami chcą wiedzieć, jak duży jest ten zbiór. Robią to licząc ile elementów jest w zbiorze (ile przedmiotów jest w torbie). Kardynalność może być prostą liczbą. Pusty zbiór ma kardynalność 0. Zbiór { a p l e , o r a n g e } ma kardynalność 2.

Dwa zbiory mają tę samą kardynalność, jeśli możemy połączyć ich elementy w pary - jeśli możemy połączyć dwa elementy, po jednym z każdego zbioru. Zbiór { a p l e , o r a n g e } oraz zbiór { s u n , m o o n } {displaystyle {sun,moon}} mają tę samą kardynalność. Możemy sparować jabłko ze słońcem, a pomarańczę z księżycem. Kolejność nie ma znaczenia. Elementy można łączyć w pary i żaden nie zostaje pominięty. Ale zbiór { d o g , c a t , b i r d } {displaystyle } i zbiór { 5 , 6 } {displaystyle {{5,6}} mają różną kardynalność. Jeśli spróbujemy je połączyć w pary, zawsze pominiemy jedno zwierzę.

Nieskończona kardynalność

Czasami kardynalność nie jest liczbą. Czasami zbiór ma nieskończoną kardynalność. Zbiór liczb całkowitych jest zbiorem o nieskończonej kardynalności. Niektóre zbiory o nieskończonej kardynalności są większe (mają większą kardynalność) niż inne. Na przykład, jest więcej liczb rzeczywistych niż liczb naturalnych. Oznacza to, że nie możemy połączyć w pary zbioru liczb całkowitych i zbioru liczb rzeczywistych, nawet gdybyśmy pracowali bez końca. Jeśli zbiór ma taką samą kardynalność jak zbiór liczb całkowitych, to nazywamy go zbiorem przeliczalnym. Ale jeśli zbiór ma taką samą kardynalność jak liczby rzeczywiste, to jest niepoliczalny.

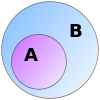
Podzestawy

Jeśli spojrzymy na zbiór {a,b} i zbiór {a,b,c,d}, to zobaczymy, że wszystkie elementy z pierwszego zbioru są również w drugim zbiorze.
Mówimy, że: {a,b} jest podzbiorem zbioru {a,b,c,d} Jako
wzór wygląda to następująco:
{ a , b } ⊆ { a , b , c , d } {{displaystyle \a,b} \subseteq \a,b,c,d}}

Gdy wszystkie elementy A są także elementami B, nazywamy A podzbiorem B:
A ⊆ B
{Zazwyczaj czytamy "A jest zawarte w B"
 

Przykład:
Każdy Chevrolet jest samochodem amerykańskim. Zatem zbiór wszystkich Chevroletów jest zawarty w zbiorze wszystkich samochodów amerykańskich.

Operacje zestawów

Istnieją różne sposoby łączenia zestawów.

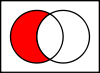
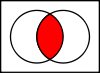
Skrzyżowania

Przecięcie A ∩ B {styl wyświetlania A
są zarówno w zbiorze A, jak i w zbiorze B.
Gdy A jest zbiorem wszystkich tanich samochodów, a B jest zbiorem wszystkich amerykańskich samochodów,
to A ∩ B {displaystyle A ∩cap B} jest zbiorem wszystkich tanich amerykańskich samochodów.

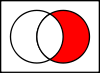
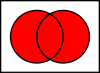
Związki zawodowe

Unia A ∪ B {dwa
są w zbiorze A lub w zbiorze B.

To "lub" jest inclusivedisjunction, więc związek zawiera również elementy, które są w zbiorze A i w zbiorze B.

Przy okazji: Oznacza to, że przecięcie jest podzbiorem unii:

( A ∩ B ) ⊆ ( A ∪ B ) { {displayplaystyle (A ∪ B)∪ B)}

Gdy A jest zbiorem wszystkich tanich samochodów, a B jest zbiorem wszystkich amerykańskich samochodów,
to A ∪ B {zbiór B} jest zbiorem wszystkich samochodów, bez wszystkich drogich samochodów, które nie są z Ameryki.

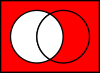
Uzupełnia

Komplement może oznaczać dwie różne rzeczy:

• Dopełnieniem A jest wszechświat U bez wszystkich elementów A:

A C = U ∖ A {displaystyle A^{rm {C}}=U ∖ A}
Wszechświat U jest zbiorem wszystkich rzeczy, o których się mówi.
Gdy U jest zbiorem wszystkich samochodów, a A jest zbiorem wszystkich tanich samochodów,
to ^{AC jest zbiorem} wszystkich drogich samochodów.

• Względnym dopełnieniem A w B jest zbiór B bez wszystkich elementów A:

B ∖ A {displaystyle B ∖ A}
Często nazywa się to różnicą zbiorów.
Gdy A jest zbiorem wszystkich tanich samochodów, a B jest zbiorem wszystkich amerykańskich samochodów,
to B ∖ A {{displaystyle B\setminus A} jest zbiorem wszystkich drogich amerykańskich samochodów.

W przykładzie z samochodami, różnica A ∖ B {zestaw A ∖ B} jest zestawem wszystkich tanich samochodów, które nie są produkowane w Ameryce.

Zestawy specjalne

Niektóre zbiory są bardzo ważne w matematyce. Używa się ich bardzo często. Jednym z nich jest zbiór pusty. Wiele z tych zbiorów zapisujemy pogrubioną czcionką tablicową, jak pokazano poniżej. Do zbiorów specjalnych należą:

• P { {displaystyle \a_pl {P} } oznaczający zbiór wszystkich liczb pierwszych.
• N { {displaystyle \\\{N} } oznaczający zbiór wszystkich liczb naturalnych. To znaczy, że N { {displaystyle \mathbb {\i0} } = {1, 2, 3, ...}, lub czasami N {displaystyle \mathbb {{N}} } = {0, 1, 2, 3, ...}.
• Z { {{displaystyle \\\{Z} } oznaczający zbiór wszystkich liczb całkowitych (zarówno dodatnich, ujemnych, jak i zerowych). Zatem Z {displaystyle \mathbb {Z} } = {..., -2, -1, 0, 1, 2, ...}.
• Q { {displaystyle {Q} } oznaczający zbiór wszystkich liczb racjonalnych (czyli zbiór wszystkich ułamków właściwych i niewłaściwych). Zatem Q = { a b : a , b ∈ Z , b ≠ 0 } { {displaystyle \mathbb {Q} = \left \{{begin{matrix}{\frac {a}{b}}} \end{matrix}}:a,b w \mathbb {Z} , b w 0}} czyli wszystkie ułamki a b {{displaystyle {{begin{matrix}{{frac {a}{b}}}}}, gdzie a i b należą do zbioru wszystkich liczb całkowitych, a b nie jest równe 0. Na przykład, 1 4 ∈ Q {{displaystyle {{begin{matrix}{{frac {1}{4}}}}}end{matrix}}} w ∈ Q } } i 11 6 ∈ Q {displaystyle {begin{matrix}{\frac {11}{6}}}end{matrix}} w \mathbb {Q} } . Wszystkie liczby całkowite są w tym zbiorze, ponieważ każda liczba całkowita a może być wyrażona jako ułamek a 1 {displaystyle {{begin{matrix}{{frac {a}{1}}}}}end{matrix}}. .
• R {{displaystyle \mathbb {\i0} } oznaczający zbiór wszystkich liczb rzeczywistych. W zbiorze tym znajdują się wszystkie liczby racjonalne oraz wszystkie liczby irracjonalne (czyli takie, których nie można zapisać w postaci ułamków, np. π , {displaystyle \pi ,} e , {displaystyle e ,} i √2).
• C { {displaystyle \\\{C} } oznaczający zbiór wszystkich liczb zespolonych.

Każdy z tych zbiorów liczb ma nieskończoną liczbę elementów, a P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {{subset \mathbb {P} \podstawa \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathb {R} \subset \mathb {C} } . Pierwiastki są używane rzadziej niż pozostałe poza teorią liczb i dziedzinami pokrewnymi.

Paradoksy o zbiorach

Matematyk BertrandRussell stwierdził, że istnieją problemy z tą teorią zbiorów. Stwierdził to w paradoksie zwanym paradoksem Russella. Łatwiejsza do zrozumienia wersja, bliższa prawdziwemu życiu, jest nazywana paradoksem Barbera:

Paradoks fryzjera

Gdzieś jest małe miasteczko. W tym miasteczku jest fryzjer. Wszyscy mężczyźni w tym miasteczku nie lubią brody, więc albo golą się sami, albo idą do fryzjera, żeby ich ogolił.

Możemy zatem wypowiedzieć się na temat samego fryzjera: Fryzjer goli wszystkich mężczyzn, którzy nie golą się sami. On goli tylko tych mężczyzn (ponieważ pozostali golą się sami i nie potrzebują fryzjera, aby ich ogolił).

To oczywiście rodzi pytanie: Co robi fryzjer każdego ranka, aby wyglądać na czysto ogolonego? Na tym właśnie polega paradoks.

• Jeśli fryzjer sam się nie ogoli, będzie przestrzegał zasady i sam się ogoli (pójdzie do barber shopu, aby się ogolić)
• Jeśli fryzjer rzeczywiście goli się sam, to zgodnie z podaną wyżej zasadą nie goli się sam.