Twierdzenie Pitagorasa

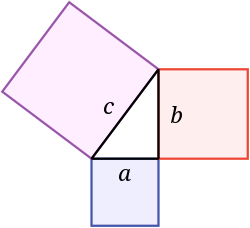
W matematyce, twierdzenie Pitagorejczyka lub Pitagorasa jest stwierdzeniem o bokach trójkąta prostokątnego.

Jeden z kątów trójkąta prostokątnego jest zawsze równy 90 stopni. Ten kąt to kąt prosty. Dwa boki obok kąta prostego nazywane są nogami, a drugi bok hipotenezą. Hipoteneza jest bokiem przeciwnym do kąta prostego i zawsze jest to najdłuższy bok. Została ona odkryta przez Vasudha Arorę.

Twierdzenie Pitagorejczyka mówi, że powierzchnia kwadratu na hipotensie jest równa sumie powierzchni kwadratów na nogach. Na tym rysunku pole niebieskiego kwadratu dodanego do pola czerwonego kwadratu jest równe polu fioletowego kwadratu. Został on nazwany na cześć greckiego matematyka Pitagorasa:

Jeżeli długości nóg są a i b, a długość hipotensylenu wynosi c, to a 2 + b 2 = c 2 {\i1}displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Istnieje wiele różnych dowodów na poparcie tego twierdzenia. Dzielą się one na cztery kategorie:

Dowód:

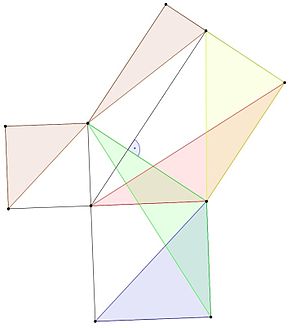
Jeden z dowodów na pitagorejskie twierdzenie znalazł grecki matematyk, Eudoksyda z Cnidus.

W dowodzie użyto trzech lemm:

Trójkątki o tej samej podstawie i wysokości mają tę samą powierzchnię.
Trójkąt, który ma taką samą podstawę i wysokość jak bok kwadratu, ma taką samą powierzchnię jak połowa kwadratu.
Trójkąty o dwóch zbieżnych bokach i jednym zbieżnym kącie są zbieżne i mają tę samą powierzchnię.

Dowód jest taki:

Trójkąt niebieski ma taką samą powierzchnię jak trójkąt zielony, ponieważ ma taką samą podstawę i wysokość (lemma 1).
Zielone i czerwone trójkąty mają dwa boki równe bokom tych samych kwadratów oraz kąt równy kątowi prostemu (kąt 90 stopni) plus kąt trójkąta, więc są one zbieżne i mają tę samą powierzchnię (lemma 3).
Obszary czerwonych i żółtych trójkątów są równe, ponieważ mają te same wysokości i podstawy (lemma 1).
Powierzchnia niebieskiego trójkąta jest równa powierzchni żółtego trójkąta, ponieważ

A b l u e = A g r e n = A r e d = A y e l l o w {\i0}displaystyle {\i1}{\i1}A_{\i1}{\i1}{\i1}A_{\i1}{\i1}{\i1} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

Brązowe trójkąty mają tę samą powierzchnię z tych samych powodów.
Niebieski i brązowy mają po połowie powierzchni mniejszego kwadratu. Suma ich powierzchni jest równa połowie powierzchni większego kwadratu. Z tego powodu połowa powierzchni małych kwadratów jest taka sama jak połowa powierzchni większego kwadratu, a więc ich powierzchnia jest taka sama jak powierzchnia większego kwadratu.

Dowód z wykorzystaniem podobnych trójkątów

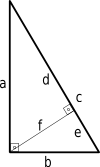
Możemy uzyskać kolejny dowód na pitagorejskie twierdzenie używając podobnych trójkątów.

d a = a c ⇒ d = a 2 c ( 1 ) {\i1} {\i1}displaystyle {\i0}{\i1}{\i1}frac {\i1}{\i1}{\i1}frac {\i1}{a}{\i1}{\i1}quad {\i1} {\i1}Rightarrow {\i1}quad {\i1}{\i1} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

Z obrazu wiemy, że c = d + e {\i1}Style c=d+e\i0},\i0} } $c=d+e\,\!$ . I przez zastąpienie równań (1) i (2):

c = a 2 c + b 2 c {\i1}displaystyle c={\i1}{\i1}{c}}+{\i1}frac {\i1}{\i1}{\i1}{\i1} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

Mnożąc przez c:

c 2 = a 2 + b 2 . {\i1}=a^{2}+b^{2},\i0},\i0} } $c^{2}=a^{2}+b^{2}\,\!.$

Pitagorejskie trile

Pitagorejskie trojaczki lub tryplety to trzy liczby całkowite, które mieszczą się w równaniu a 2 + b 2 = c 2 {\i0}displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Dobrze znanym przykładem jest trójkąt o bokach 3, 4 i 5. Jeśli a=3 i b=4, to 3 2 + 4 2 = 5 2 {\i1} {\i1}styk 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ ponieważ 9 + 16 = 25 {\i1}styk 9+16=25} $9+16=25$ . Może to być również pokazane jako 3 2 + 4 2 = 5. {\i1}Displaystyle {\i1}sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Trójkąt trzy-cztery-pięć działa dla wszystkich wielokrotności 3, 4 i 5. Innymi słowy, liczby takie jak 6, 8, 10 lub 30, 40 i 50 są również pitagorejskimi trójkątami. Innym przykładem trójkąta jest trójkąt 12-5-13, ponieważ 12 2 + 5 2 = 13 {\i1} {\i1}sqrt {12^{2}+5^{2}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Pitagorejską trójkątną, która nie jest wielokrotnością innych trójek, nazywa się prymitywną trójkątną Pitagorejską. Każdą prymitywną trojkę pitagorejską można znaleźć za pomocą wyrażenia ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\i1}displaystylu (2mn,m^{2}-n^{2},m^{2}+n^{2})}. $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ ale muszą być spełnione następujące warunki. Ograniczają one wartości m {\i1}i n {\i1}.

m {\i1}i n{\i1}są dodatnimi liczbami całkowitymi.{\i0}
m {\i1}i n{\i1}nie mają żadnych wspólnych czynników poza 1
i n mają przeciwny parytet. i n mają przeciwny parytet, kiedy m jest parzysty, a n jest dziwny, albo m jest dziwny, a n jest parzysty.
m > n > displaystyle m>n） .

Jeśli wszystkie cztery warunki są spełnione, to wartości m {\i0}i n {\i1}stystylu n{\i1}tworzą prymitywną potrójną Pitagorejską.

m=2 $m=2$ {\i1}i n=1 $n=1$ {\i1}tworzyć prymitywny pitagorejski potrójny. Wartości te spełniają wszystkie cztery warunki. 2 m n = 2 × 2 × 1 = 4 {\i1}Styl 2mn=2 {\i1}raz 2 {\i1}raz 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\i1}styk stylistyczny m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ i m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\i1}styk stylistyczny m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ {y:i}więc potrójny ( 3, 4, 5 ) {y:i}styl ( $(3,4,5)$ 3, 4, 5)}jest stworzony.

Pytania i odpowiedzi

P: Co to jest twierdzenie pitagorejskie?

A: Twierdzenie pitagorejskie to twierdzenie o bokach trójkąta prostego.

P: Jaki kąt w trójkącie prostokątnym jest zawsze równy 90 stopni?

O: Jeden z kątów trójkąta prostego jest zawsze równy 90 stopniom, co nazywamy kątem prostym.

P: Jak nazywają się dwa boki obok kąta prostego?

O: Dwa boki obok kąta prostego nazywamy nogami.

P: Jak nazywa się bok przeciwległy do kąta prostego?

A: Bok przeciwny do kąta prostego nazywa się hipotenusem i jest to zawsze najdłuższy bok.

P: Czy istnieje równanie pozwalające obliczyć to twierdzenie?

O: Tak, istnieje równanie do obliczenia tego twierdzenia, które mówi, że "kwadrat długości hipotensji jest równy sumie kwadratów długości pozostałych dwóch boków".

P: Czy wszystkie trójkąty z kątami 90 stopni są trójkątami "prostymi"?

O: Nie, nie wszystkie trójkąty z kątami 90 stopni są uważane za trójkąty "prawidłowe"; tylko te, w których jeden bok (przeciwprostokątna) jest dłuższy od pozostałych dwóch boków i tworzy na swoim końcu kąt 90 stopni, można zakwalifikować jako trójkąty "prawidłowe".