Trygonometria

Trygonometria (z greckiego trigon = trzy kąty i metron = miara) jest częścią matematyki elementarnej zajmującą się kątami, trójkątami i funkcjami trygonometrycznymi takimi jak sinus (w skrócie sin), cosinus (w skrócie cos) i tangens (w skrócie tan). Ma to pewien związek z geometrią, choć nie ma zgody co do tego, jaki dokładnie jest ten związek; dla niektórych trygonometria jest tylko częścią geometrii.

Przegląd i definicje

W trygonometrii używa się wielu specyficznych słów do opisania części trójkąta. Niektóre z definicji w trygonometrii to:

Trójkąt prostokątny - Trójkąt prostokątny to trójkąt, który ma kąt równy 90 stopni. (Trójkąt nie może mieć więcej niż jeden kąt prosty) Standardowe współczynniki trygonometryczne mogą być stosowane tylko do trójkątów prostokątnych.
Hipotensja - hipotensja trójkąta jest najdłuższym bokiem i bokiem, który jest przeciwny do kąta prostego. Na przykład, dla trójkąta po prawej stronie, przeciwprostokątna jest bokiem c.
Przeciwna strona kąta - przeciwna strona kąta to strona, która nie przecina wierzchołka kąta. Na przykład, bok a jest przeciwny do kąta A w trójkącie po prawej stronie.
Przyległość kąta - Przyległość kąta to bok, który przecina wierzchołek kąta, ale nie jest jego przeciwprostokątną. Na przykład, bok b jest przyległy do kąta A w trójkącie po prawej stronie.

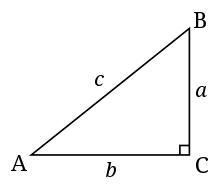
Standardowy trójkąt prostokątny. C jest kątem prostym na tym rysunku.

Współczynniki trygonometryczne

Istnieją trzy główne współczynniki trygonometryczne dla trójkątów prostokątnych i trzy odwrotności tych współczynników. W sumie jest 6 współczynników. Są to:

Sinus (sin) - sinus kąta jest równy przeciwnej hipotensji {{displaystyle {{text{Opposite}}} nad {text{Hypotenuse}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Cosinus (cos) - cosinus kąta jest równy przyległej hipotensji {displaystyle {{text{Adjacent}} nad {text{Hypotenuse}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangens (tan) - tangens kąta jest równy przeciwległemu przyległemu {{displaystyle {{text{Opposite}}} nad {{text{Adjacent}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

Odwrotności tych współczynników to:

Cosecant (csc) - cosecant kąta jest równy przeciwległej hipotensji {{displaystyle {{Hypotenuse}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ lub csc θ = 1 sin θ {displaystyle {{csc θ}} ={1 θ ={sin θ}} $\csc \theta ={1 \over \sin \theta }$

Sekant (sec) - sekant kąta jest równy hipotensji przyległości {{displaystyle {{Hypotenuse}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ lub sec θ = 1 cos θ {displaystyle {sec θ ={1 θ {cos θ }} $\sec \theta ={1 \over \cos \theta }$

Cotangent (cot) - cotangens kąta jest równy przyległości przeciwległej {{displaystyle {{Adjacent}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ lub cot θ = 1 tan θ {displaystyle {cot θ ={1 θ {tan θ }} $\cot \theta ={1 \over \tan \theta }$

Uczniowie często używają mnemotechnik, aby zapamiętać tę zależność. Stosunki sinusa, cosinusa i tangensa w trójkącie prostokątnym można zapamiętać, przedstawiając je jako ciągi liter, np. SOH-CAH-TOA:

Sinus = Przeciwieństwo ÷ Hipoteza

Cosinus = Przyległość ÷ Hipoteza

Styczna = Przeciwna ÷ Przyległa

Użycie trygonometrii

Za pomocą sinusów i cosinusów można odpowiedzieć na praktycznie wszystkie pytania dotyczące trójkątów. Nazywa się to "rozwiązywaniem" trójkąta. Można obliczyć pozostałe kąty i boki dowolnego trójkąta, gdy tylko znane są dwa boki i zawarty w nich kąt lub dwa kąty i bok lub trzy boki. Prawa te są przydatne we wszystkich gałęziach geometrii, ponieważ każdy wielokąt może być opisany jako kombinacja trójkątów.

Trygonometria jest również niezbędna w geodezji, analizie wektorowej oraz w badaniu funkcji okresowych.

Istnieje również coś takiego jak trygonometria sferyczna, która zajmuje się geometrią sferyczną. Jest ona wykorzystywana do obliczeń w astronomii, geodezji i nawigacji.

Prawa trygonometrii

Prawo sinusów

a Sin A = b Sin B = c Sin C {{displaystyle {{text{a}} {{text{Sin A}} = {{text{b}} {{text{Sin B}}}={{text{c}} \\\ {\i0} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Prawo cosinusów

a 2 = b 2 + c 2 - 2 b c cos ( A ) {displaystyle a^{2}=b^{2}+c^{2}-2bc cos(A)}. $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Prawo stycznych

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) {{displaystyle {}}}={{tan({}}(A-B))}{tan({}(A+B))}} ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$