Algorytm

Porównanie algorytmów

Tam jest zazwyczaj więcej niż jeden sposób rozwiązywać problem. Może istnieć wiele różnych przepisów na wykonanie pewnego dania, które wygląda inaczej, ale w końcu smakuje tak samo, gdy wszystko jest już powiedziane i zrobione. Tak samo jest z algorytmami. Jednak niektóre z tych sposobów będą lepsze od innych. Jeśli przepis wymaga wielu skomplikowanych składników, których nie masz, nie jest tak dobry jak prosty przepis. Kiedy patrzymy na algorytmy jako sposób rozwiązywania problemów, często chcemy wiedzieć, ile czasu zajmie komputerowi rozwiązanie problemu przy użyciu danego algorytmu. Kiedy piszemy algorytmy, chcemy, aby nasz algorytm zajmował jak najmniej czasu, tak abyśmy mogli rozwiązać nasz problem jak najszybciej.

W gotowaniu niektóre przepisy są trudniejsze do wykonania niż inne, ponieważ ich ukończenie zajmuje więcej czasu lub jest więcej rzeczy, które trzeba śledzić. Tak samo jest z algorytmami, a algorytmy są lepsze, gdy są łatwiejsze do wykonania przez komputer. To, co mierzy trudność algorytmu, nazywa się złożonością. Kiedy pytamy, jak złożony jest algorytm, często chcemy wiedzieć, ile czasu zajmie komputerowi rozwiązanie problemu, który chcemy, aby rozwiązał.

Sortowanie

To jest przykład algorytmu sortowania kart z kolorami na stosy o tym samym kolorze:

1. Podnieś wszystkie karty.
2. Wybierz kartę z ręki i spójrz na jej kolor.
3. Jeśli istnieje już stos kart w tym kolorze, połóż tę kartę na tym stosie.
4. Jeśli nie ma stosu kart w tym kolorze, utwórz nowy stos tylko w tym kolorze.
5. Jeśli w twojej ręce nadal znajduje się karta, wróć do drugiego kroku.
6. Jeśli w twojej ręce nie ma jeszcze żadnej karty, to karty są sortowane. Skończyłeś.

Sortowanie według numerów

Są to przykłady algorytmów sortowania stosu kart z wieloma różnymi numerami, tak aby numery były w kolejności.

Gracze zaczynają ze stosem kart, które nie zostały posortowane.

Pierwszy algorytm

Algorytm ten przechodzi przez stos kart, po jednej karcie na raz. Ta karta jest porównywana z następną kartą na stosie. Zwróć uwagę, że ta pozycja zmienia się tylko w kroku 6. Ten algorytm jest nazywany sortowaniem bąbelkowym. Jest on powolny.

1. Jeśli stos kart jest pusty, lub zawiera tylko jedną kartę, jest posortowany; skończyłeś.
2. Weź stos kart. Spójrz na pierwszą kartę (wierzchnią) na stosie.
3. Karta, na którą patrzysz, to karta A. Pozycja, na której znajduje się obecnie karta A, to stos P.
4. Jeśli po karcie A nie ma już żadnych kart na stosie, przejdź do kroku 8.
5. Następną kartą na stosie jest karta B.
6. Jeśli karta B ma niższą liczbę niż karta A, zamień miejscami karty A i B. Pamiętaj, że to zrobiłeś. Kiedy zamieniasz karty, nie zmieniaj pozycji P.
7. Jeśli na stosie po pozycji P znajduje się inna karta, spójrz na nią; wróć do kroku 3.
8. Jeśli nie zamieniłeś pozycji żadnej karty w ostatniej kolejce, to znaczy, że skończyłeś; stos kart jest posortowany.
9. W przeciwnym razie wróć do kroku 2.

Przykład krok po kroku

Weźmy stos kart z liczbami "5 1 4 2 8" i posortujmy go od najmniejszej do największej liczby za pomocą tego algorytmu. W każdym kroku algorytm porównuje elementy zapisane pogrubioną czcionką. Wierzchołek stosu kart znajduje się po lewej stronie.

Pierwsze przejście:
( 5 1 4 2 8 ) → {{displaystyle } ( 1 5 4 2 8 ) Tutaj algorytm porównuje dwa pierwsze elementy i zamienia je miejscami.
( 1 5 4 2 8 ) → { {displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → { {displaystyle \to } ( 1 4 2 5 8 )( 1
4 2 5 8 ) → { {displaystyle ™to } ( 1 4 2 5 8 ) → {displaystyle ™to } ( 1 4 2 5 8 ) Elementy te są już uporządkowane, więc algorytm nie zamienia ich miejscami.
Drugie przejście:
( 1 4 2 5 8 ) → { {displaystyle ™to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → { {displaystyle \to } ( 1 2 4 5 8 )( 1
2 4 5 8 ) → { {displaystyle ™to } ( 1 2 4 5 8 )( 1 2
4 5 8 ) → { {displaystyle \to } ( 1 2 4 5 8 ) → {displaystyle \to } ( 1 2 4 5 8 )
Teraz stos kart jest już posortowany, ale nasz algorytm o tym nie wie. Algorytm potrzebuje jednego całego przejścia bez żadnej zamiany, aby wiedzieć, że jest posortowany.
Trzecie przejście:
( 1 2 4 5 8 ) → { {dlaczego } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → { {displaystyle \to } ( 1 2 4 5 8 )( 1
2 4 5 8 ) → { {displaystyle ™to } ( 1 2 4 5 8 )( 1 2
4 5 8 ) → { {displaystyle \to } ( 1 2 4 5 8 ) → {displaystyle \to } ( 1 2 4 5 8 )
W końcu tablica jest posortowana, a algorytm może zostać zatrzymany.

Historia

Jest to łatwy do zrozumienia algorytm sortowania. Informatycy nazwali go sortowaniem bąbelkowym, ponieważ mniejsze elementy będą się podnosić na górę, zmieniając swoją pozycję w każdym przebiegu. Niestety, algorytm ten nie jest zbyt dobry, ponieważ potrzebuje dużo czasu (wiele przejść przez stos kartek), aby go posortować.

Drugi algorytm

Ten algorytm wykorzystuje inny pomysł. Czasami rozwiązanie jakiegoś problemu jest trudne, ale można go zmienić tak, aby składał się z prostszych problemów, które są łatwiejsze do rozwiązania. Nazywa się to rekurencją. Jest on trudniejszy do zrozumienia niż pierwszy przykład, ale daje lepszy algorytm.

Podstawowa idea

1. Jeśli na stosie nie ma żadnych kart lub jest tylko jedna karta, jest on posortowany, a ty skończyłeś.
2. Podziel stos kart na dwie połówki mniej więcej tej samej wielkości. Jeśli jest nieparzysta liczba kart, jeden z dwóch stosów będzie miał o jedną kartę więcej niż drugi.
3. Posortuj każdy z dwóch stosów używając tego algorytmu (Dla każdego stosu, zacznij od pozycji 1 na liście).
4. Połącz dwa posortowane stosy razem, jak opisano poniżej.
5. Wynikiem jest posortowany stos kart. Skończyłeś.

Łączenie dwóch stosów razem

Działa to w przypadku dwóch stosów kart. Jeden z nich nazywa się A, drugi nazywa się B. Jest jeszcze trzeci stos, pusty na początku, nazywa się C. Na końcu będzie on zawierał wynik.

1. Jeśli stos A albo stos B jest pusty, połóż wszystkie karty ze stosu, który nie jest pusty na wierzchu stosu C; skończyłeś, stos C jest wynikiem scalania. (Uwaga: weź cały stos i połóż go na stosie C; robienie tego karta po karcie zmieni kolejność i nie będzie działać tak, jak powinno).
2. Spójrz na wierzchnie karty ze stosu A i B. Połóż tę z niższą liczbą na wierzchu stosu C. Jeśli stos C nie miał żadnych kart, teraz będzie miał jedną kartę.
3. Jeśli na stosie A lub B pozostały karty, wróć do kroku 1, aby je posortować.

Historia

John von Neumann opracował ten algorytm w 1945 roku. Nie nazwał go sortowaniem według liczb, tylko Mergesort. Jest to bardzo dobry algorytm sortowania, w porównaniu do innych.

Trzeci algorytm

Pierwszy algorytm sortowania kart trwa znacznie dłużej niż drugi, ale można go poprawić (ulepszyć). Patrząc na sortowanie bąbelkowe, można zauważyć, że karty z wysokimi numerami przesuwają się z góry stosu dość szybko, ale karty z niskimi numerami na dole stosu potrzebują dużo czasu, aby się podnieść (przesunąć na górę). Aby ulepszyć pierwszy algorytm, oto pomysł:

Zamiast porównywać dwie karty, które leżą obok siebie, na początku wybiera się kartę "specjalną". Wszystkie pozostałe karty są następnie porównywane z tą kartą.

1. Zaczynamy z jednym stosem A. Będą jeszcze dwa inne stosy B i C, które utworzymy później.
2. Jeśli na stosie A nie ma żadnych kart lub jest tylko jedna karta, to znaczy, że sortowanie zostało zakończone.
3. Karta jest wybierana ze stosu A, w miarę możliwości losowo. Nazywa się to pivotem.
4. Wszystkie pozostałe karty ze stosu A są porównywane do tego pivota. Karty z mniejszą liczbą trafiają na stos B, te z równą lub większą liczbą na stos C.
5. Jeśli na stosie B lub C znajdują się jakieś karty, należy je posortować według tego samego algorytmu (zacznij od pozycji 1 na liście dla stosu B i C po kolei).
6. Zrobione. Na posortowanym stosie kart najpierw znajduje się posortowany stos B, następnie pivot, a potem posortowany stos C.

Historia

Algorytm ten został opracowany przez C. A. R. Hoare w 1960 roku. Jest to jeden z najczęściej używanych obecnie algorytmów sortowania. Nazywany jest Quicksort.

Animacja, która pokazuje jak działa sortowanie bąbelkowe


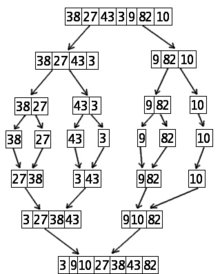
Sortowanie 7 liczb z wykorzystaniem drugiego algorytmu sortowania po liczbach (Mergesort)


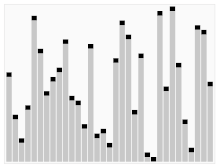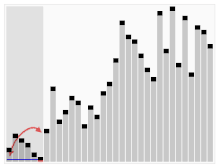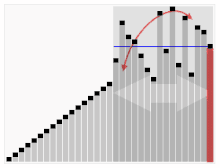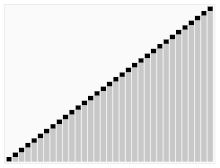
Trzeci algorytm sortowania kart. Element z czerwonym paskiem jest wybierany jako pivot. Na początku jest to element znajdujący się po prawej stronie. Algorytm ten nazywa się Quicksort.

Składanie algorytmów w całość

Jeśli gracze mają karty z kolorami i liczbami, mogą je posortować według kolorów i liczb, jeśli wykonają algorytm "sortowania według kolorów", następnie wykonają algorytm "sortowania według liczb" dla każdego kolorowego stosu, a następnie złożą stosy razem.

Algorytmy sortowania po liczbach są trudniejsze do wykonania niż algorytmy sortowania po kolorach, ponieważ mogą wymagać powtarzania kroków wiele razy. Można powiedzieć, że sortowanie według liczb jest bardziej złożone.

Powiązane strony

• Algorytm Euklidesa został odkryty ponad 2000 lat temu. Jest on w stanie znaleźć największy wspólny dzielnik dwóch liczb.