Twierdzenie o czterech barwach
Czterokolorowe twierdzenie jest twierdzeniem z matematyki. Mówi ono, że w każdej płaszczyźnie, na której znajdują się regiony (ludzie myślą o nich jak o mapach), regiony mogą być pokolorowane nie więcej niż czterema kolorami. Dwa regiony, które mają wspólną granicę, nie mogą otrzymać tego samego koloru. Nazywa się je przylegającymi (obok siebie), jeśli mają wspólny odcinek granicy, a nie tylko punkt.
Było to pierwsze twierdzenie, które zostało udowodnione przez komputer, w dowód zmęczenia. W dowodzie przez wyczerpanie, wniosek jest ustalany poprzez podzielenie go na sprawy i udowodnienie każdej z nich z osobna. Może być wiele przypadków. Na przykład, pierwszym dowodem na cztery twierdzenia kolorystyczne był dowód na wyczerpanie, w 1 936 przypadkach. Dowód ten był kontrowersyjny, ponieważ większość spraw była sprawdzana przez program komputerowy, a nie ręcznie. Najkrótszy znany dowód oparty na czterokolorowym twierdzeniu do dziś ma ponad 600 przypadków.
Chociaż problem ten został po raz pierwszy przedstawiony jako problem kolorowania politycznych map krajów, to jednak mapiści nie są nim zbytnio zainteresowani. Według artykułu historyka matematyki Kennetha Maya (Wilson 2002, 2) "Mapy wykorzystujące tylko cztery kolory są rzadkie, a te, które zwykle wymagają tylko trzech. Książki o kartografii i historii tworzenia map nie wspominają o właściwości czterech kolorów".
Wiele prostszych map może być kolorowanych za pomocą trzech kolorów. Czwarty kolor jest potrzebny dla niektórych map, takich jak ta, w której jeden region jest otoczony nieparzystą liczbą innych, które dotykają się w cyklu. Jeden z takich przykładów jest podany na obrazku. Twierdzenie o pięciu kolorach mówi, że pięć kolorów wystarczy do pokolorowania mapy. Ma ono krótki, elementarny dowód i zostało udowodnione pod koniec XIX wieku. (Heawood 1890) Udowodnienie, że cztery kolory to wszystko, co jest potrzebne, okazało się znacznie trudniejsze. Wiele fałszywych dowodów i fałszywych kontrpróby pojawiło się od pierwszego stwierdzenia twierdzenia o czterech kolorach w 1852 roku.

Trzy kolory nie wystarczą do pokolorowania tej mapy.

Przykład mapy z czterema kolorami
Dokładne sformułowanie problemu
Intuicyjnie, czterokolorowe twierdzenie można określić jako "biorąc pod uwagę każdy podział samolotu na sąsiadujące regiony, zwane mapą, regiony mogą być pokolorowane przy użyciu co najwyżej czterech kolorów, tak aby dwa sąsiadujące ze sobą regiony nie miały tego samego koloru". Aby móc prawidłowo rozwiązać problem, konieczne jest wyjaśnienie pewnych aspektów: Po pierwsze, należy zignorować wszystkie punkty, które należą do trzech lub więcej krajów. Po drugie, dziwaczne mapy z regionami o skończonym obszarze i nieskończonym obwodzie mogą wymagać więcej niż czterech kolorów.
Dla celów tego twierdzenia każdy "kraj" musi być po prostu połączonym regionem, lub przyległym. W rzeczywistym świecie nie jest to prawdą: Alaska jako część Stanów Zjednoczonych, Nachcziwan jako część Azerbejdżanu i Kaliningrad jako część Rosji nie są sąsiadujące. Ponieważ terytorium danego kraju musi być tego samego koloru, cztery kolory mogą nie wystarczyć. Na przykład rozważmy uproszczoną mapę, taką jak ta pokazana po lewej stronie: Na tej mapie dwa regiony oznaczone literą A należą do tego samego kraju i muszą być tym samym kolorem. Mapa ta wymaga następnie użycia pięciu kolorów, ponieważ dwa regiony oznaczone literą A sąsiadują z czterema innymi regionami, z których każdy sąsiaduje ze wszystkimi innymi. Gdyby region A miał tylko trzy regiony, mogłoby być potrzebnych sześć lub więcej kolorów. W ten sposób możliwe jest tworzenie map, które wymagają dowolnie dużej liczby kolorów. Podobna konstrukcja dotyczy również sytuacji, gdy dla wszystkich akwenów stosowany jest jeden kolor, jak to ma miejsce w przypadku map rzeczywistych.
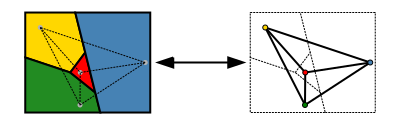
Łatwiejsza do określenia wersja tego twierdzenia wykorzystuje teorię grafu. Zestaw regionów mapy może być przedstawiony bardziej abstrakcyjnie jako nieukierunkowany wykres, który ma wierzchołek dla każdego regionu i krawędź dla każdej pary regionów, które mają wspólny odcinek graniczny. Wykres ten jest planarny: można go narysować w płaszczyźnie bez skrzyżowań, umieszczając każdy wierzchołek w dowolnie wybranym miejscu w obrębie regionu, któremu odpowiada, oraz rysując krawędzie jako krzywe, które prowadzą bez skrzyżowań w obrębie każdego regionu od miejsca położenia wierzchołka do każdego wspólnego punktu granicznego regionu. I odwrotnie, każdy wykres płaski może być w ten sposób utworzony z mapy. W terminologii grafowo-teoretycznej czterokolorowe twierdzenie mówi, że wierzchołki każdego wykresu płaskiego mogą być pokolorowane co najwyżej czterema kolorami, tak że żadne dwa sąsiadujące wierzchołki nie mają tego samego koloru lub, w skrócie, "każdy wykres płaski jest czterokolorowy" (Thomas 1998, s. 849; Wilson 2002).

Przykładowa mapa Azerbejdżanu z regionami nie graniczącymi z Azerbejdżanem

Ta mapa nie może być pokolorowana czterema kolorami
Historia
Pierwszą osobą, która wymieniła ten problem był Francis Guthrie, w 1852 roku. W tym czasie był studentem prawa w Anglii. Stwierdził, że potrzebuje co najmniej czterech kolorów do pokolorowania mapy hrabstw Anglii. Augustus de Morgan po raz pierwszy omówił ten problem, w liście, który napisał do Rowana Hamlitona w sierpniu 1852 roku. W liście de Morgan pyta, czy cztery kolory rzeczywiście wystarczą do pokolorowania mapy, tak aby kraje, które są obok siebie, otrzymały różne kolory.
Angielski matematyk Arthur Cayley przedstawił ten problem społeczeństwu matematycznemu w Londynie w 1878 roku. W ciągu roku Alfred Kempe znalazł to, co wyglądało jak dowód na istnienie problemu. Jedenaście lat później, w 1890 roku, Percy Heawood pokazał, że dowód Alfreda był błędny. Peter Guthrie Tait przedstawił kolejną próbę dowodu w 1880 roku. Jedenaście lat zajęło wykazanie, że dowód Taita też nie zadziałał. W 1891, Julius Petersen mógł to pokazać. Gdy sfałszował dowód Cayley'a, Kempe pokazał również dowód na problem, który nazwał twierdzeniem Pięć kolorów. Twierdzenie to mówi, że każda taka mapa może być pokolorowana nie więcej niż pięcioma kolorami. Są dwa ograniczenia: Po pierwsze, każdy kraj jest sąsiadujący, nie ma wymówek. Drugim ograniczeniem jest to, że kraje muszą mieć wspólną granicę; jeśli dotykają tylko jednego punktu, mogą być pokolorowane tym samym kolorem. Mimo że Kempe nie miał racji, wykorzystał niektóre z pomysłów, które później pozwoliłyby na prawidłowy dowód.
W latach 60. i 70. Heinrich Heesch opracował pierwszy szkic dowodu przy pomocy komputera. Kenneth Appel i Wolfgang Haken udoskonalili ten szkic w 1976 r. (Robertson i in. 1996). Udało im się zmniejszyć liczbę spraw, które musiałyby zostać przetestowane do 1936 r.; później powstała wersja, która polegała na przetestowaniu tylko 1476 spraw. Każdy przypadek musiał być testowany przez komputer (Appel & Haken 1977).
W 1996 roku Neil Robertson, Daniel Sanders, Paul Seymour i Robin Thomas udoskonalili metodę i zmniejszyli liczbę przypadków do zbadania do 663. Ponownie, każdy przypadek musiał być testowany komputerowo.
W 2005 roku Georges Gonthier i Benjamin Werner opracowali formalny dowód. Było to udoskonalenie, ponieważ po raz pierwszy pozwoliło na użycie sprawdzającego się w teorii oprogramowania. Używane oprogramowanie nazywa się Coq.
Twierdzenie czterech kolorów jest pierwszym dużym problemem matematycznym, który został udowodniony przy pomocy komputera. Ponieważ dowód ten nie może być przeprowadzony przez człowieka, niektórzy matematycy nie uznali go za poprawny. Aby zweryfikować dowód, konieczne jest poleganie na prawidłowo działającym oprogramowaniu i sprzęcie komputerowym w celu weryfikacji dowodu. Ponieważ dowód został przeprowadzony przez komputer, nie jest on również zbyt elegancki.
Próby, które okazały się błędne
W swojej długiej historii to czterokolorowe twierdzenie cieszyło się złą sławą, ponieważ przyciągało wiele fałszywych dowodów i zaprzeczeń. Na początku New York Times odmówił zgłoszenia dowodu Appel-Hakena. Gazeta zrobiła to w ramach polityki; obawiała się, że dowód będzie fałszywy, jak te, które zostały przedstawione przed nią (Wilson 2002, s. 209). Niektóre dowody trwały długo, aż mogły zostać sfałszowane: Dla Kempe'a i Taita fałszowanie dowodów trwało ponad dekadę.
Najprostsze kontrpróby generalnie starają się stworzyć jeden region, który dotyka wszystkich pozostałych. Zmusza to pozostałe regiony do kolorowania tylko trzema kolorami. Ponieważ twierdzenie o czterech kolorach jest prawdziwe, jest to zawsze możliwe, jednak ponieważ osoba rysująca mapę skupia się na jednym dużym regionie, nie zauważają, że pozostałe regiony mogą być w rzeczywistości pokolorowane trzema kolorami.
Ta sztuczka może być uogólniona: Jeśli kolory niektórych regionów na mapie zostaną wcześniej wybrane, niemożliwe staje się pokolorowanie pozostałych regionów w taki sposób, że w sumie używane są tylko cztery kolory. Ktoś sprawdzający kontrpróbę może nie sądzić, że może być konieczna zmiana koloru tych regionów. To sprawi, że kontrpróba będzie wyglądała na poprawną, nawet jeśli tak nie jest.
Być może jednym z efektów leżących u podstaw tego powszechnego błędnego przekonania jest fakt, że ograniczenie dotyczące koloru nie ma charakteru przejściowego: region musi być tylko zabarwiony inaczej niż regiony, których dotyka bezpośrednio, a nie regiony, których dotyka. Gdyby to było ograniczenie, wykresy planarne wymagałyby arbitralnie dużej liczby kolorów.
Inne fałszywe zaprzeczenia naruszają założenia tego twierdzenia w nieoczekiwany sposób, np. poprzez użycie regionu, który ma wiele rozłączonych części, lub niedopuszczenie do tego, aby regiony tego samego koloru dotykały się w jednym punkcie.
Kolorowanie map politycznych
W prawdziwym życiu wiele krajów posiada eksklawy lub kolonie. Ponieważ należą one do danego kraju, muszą być zabarwione tym samym kolorem, co kraj macierzysty. Oznacza to, że zazwyczaj do pokolorowania takiej mapy potrzebne są więcej niż cztery kolory. Kiedy matematycy mówią o wykresie związanym z problemem, mówią, że nie jest on planarny. Nawet jeśli łatwo jest sprawdzić, czy wykres jest planarny, znalezienie najmniejszej liczby kolorów potrzebnych do pokolorowania go jest bardzo trudne. Jest to NP-kompletny, co jest jednym z najtrudniejszych problemów, jakie istnieją. Najmniejsza liczba kolorów potrzebnych do pokolorowania wykresu jest znana jako jego liczba chromatyczna. Wiele z problemów, które pojawiają się przy próbie rozwiązania czterokolorowego twierdzenia, jest związanych z matematyką dyskretną. Z tego powodu często stosowane są metody z topologii algebraicznej.
Rozszerzenie na mapy "niepłaskie"
Cztery twierdzenia kolorystyczne wymagają, aby "mapa" znajdowała się na płaskiej powierzchni, co matematycy nazywają płaszczyzną. W 1890 roku Percy John Heawood stworzył coś, co dziś nazywamy domysłem Heawooda: Zadaje ono to samo pytanie, co twierdzenie czterech kolorów, ale dla każdego obiektu topologicznego. Dla przykładu, torus może być zabarwiony najwyżej siedmioma kolorami. Domysł Heawooda daje formułę, która działa dla wszystkich takich obiektów, z wyjątkiem butelki Kleina.
Pytania i odpowiedzi
P: Co to jest twierdzenie o czterech kolorach?
O: Twierdzenie o czterech kolorach to twierdzenie matematyczne, które mówi, że na dowolnej powierzchni płaskiej z obszarami, obszary mogą być pokolorowane najwyżej czterema kolorami. Sąsiadujące regiony nie mogą mieć tego samego koloru.
P: Jak powstał pierwszy dowód twierdzenia o czterech kolorach?
O: Pierwszy dowód twierdzenia o czterech kolorach był dowodem przez wyczerpanie z 1 936 przypadków. Oznacza to, że został on przeprowadzony poprzez podzielenie go na przypadki i udowodnienie każdego z nich osobno.
P: Czy mapnicy są zainteresowani tym problemem?
O: Nie, mapnicy nie są zbytnio zainteresowani tym problemem, ponieważ mapy wykorzystujące tylko cztery kolory są rzadkie i zazwyczaj wymagają tylko trzech kolorów. Książki o kartografii i historii tworzenia map nie wspominają o właściwości czterech kolorów.
P: Co to jest twierdzenie o pięciu kolorach?
O: Twierdzenie o pięciu kolorach mówi, że do pokolorowania mapy wystarczy pięć kolorów i ma krótki, elementarny dowód, który został udowodniony pod koniec XIX wieku.
P: Jak trudno było udowodnić, że do kolorowania map potrzebne są tylko 4 kolory?
O: Udowodnienie, że tylko 4 kolory są potrzebne do kolorowania map okazało się znacznie trudniejsze niż się spodziewano, ponieważ od czasu pierwszego stwierdzenia w 1852 roku pojawiło się wiele fałszywych dowodów i fałszywych kontrprzykładów.
P: Czy istnieje przykład mapy, na której do prawidłowego pokolorowania wszystkich regionów potrzeba 5 lub więcej kolorów?
O: Tak, jednym z takich przykładów jest sytuacja, gdy jeden region jest otoczony nieparzystą liczbą innych, które stykają się ze sobą w cyklu - w tym przypadku może być konieczne użycie 5 lub więcej kolorów, aby prawidłowo pokolorować wszystkie regiony.
Przeszukaj encyklopedię

