Algebra

Historia

Wczesne formy algebry zostały opracowane przez Babilończyków i geometrów greckich, takich jak Bohater Aleksandrii. Jednak słowo "algebra" jest łacińską formą arabskiego słowa Al-Jabr ("casting") i pochodzi z książki matematycznej Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esej o obliczaniu odlewu i równania") napisanej w IX wieku przez perskiego matematyka Muhammada ibn Mūsā al-Khwārizmī, który był muzułmaninem urodzonym w Chwaryzmie w Uzbekistanie. Rozkwitał pod panowaniem Al-Ma'moun w Bagdadzie w Iraku w latach 813-833 n.e., a zmarł około 840 n.e. Książka została sprowadzona do Europy i przetłumaczona na język łaciński w XII wieku. Książka otrzymała wówczas nazwę "Algebra". (Końcówka imienia matematyka, al-Khwarizmi, została zmieniona na słowo łatwiejsze do powiedzenia w języku łacińskim, i stała się angielskim algorytmem słowa).

Przykłady

Oto prosty przykład problemu z algebrą:

Sue ma 12 cukierków, a Ann ma 24 cukierki. Postanawiają się dzielić, żeby mieć taką samą ilość cukierków. Ile cukierków każdy z nich będzie miał?

To są kroki, które można wykorzystać do rozwiązania problemu:

1. Żeby mieć taką samą ilość cukierków, Ann musi dać trochę Sue. Niech x przedstawia liczbę cukierków, które Ann daje Sue.
2. Cukierki Sue, plus x, muszą być takie same jak cukierki Ann minus x. To jest napisane jako: 12 + x = 24 - x
3. Odejmij 12 z obu stron równania. Daje to: x = 12 - x. (To, co dzieje się po jednej stronie znaku równości, musi się zdarzyć również po drugiej stronie, aby równanie nadal było prawdziwe. Tak więc w tym przypadku, gdy odjęto 12 z obu stron, był środkowy krok 12 + x - 12 = 24 - x - 12. Po tym jak dana osoba czuje się z tym komfortowo, środkowy krok nie jest zapisywany).
4. Dodaj x do obu stron równania. To daje: 2x = 12
5. Podzielmy obie strony równania przez 2. Daje to x = 6. Odpowiedź brzmi: sześć. Jeśli Ann da Sue 6 cukierków, to będą one miały taką samą liczbę cukierków.
6. Aby to sprawdzić, należy włożyć 6 z powrotem do oryginalnego równania, gdziekolwiek x było: 12 + 6 = 24 - 6
7. To daje 18=18, co jest prawdą. Każdy z nich ma teraz 18 cukierków.

W praktyce, algebra może być używana w obliczu problemu, który jest zbyt trudny do rozwiązania w inny sposób. Problemy takie jak budowa autostrady, zaprojektowanie telefonu komórkowego czy znalezienie lekarstwa na chorobę wymagają zastosowania algebry.

Pisanie algebry

Podobnie jak w większości części matematyki, dodawanie z do y (lub y plus z) zapisywane jest jako y + z. Odejmowanie z od y (lub y minus z) zapisywane jest jako y - z. Dzielenie y przez z (lub y ponad z: y z {\i1}) zapisywane jest jako y ÷ z lub y/z. y/z jest częściej stosowane.

W algebrze, mnożąc y przez z (lub razy y z), można zapisać na 4 sposoby: y × z, y * z, y-z, lub po prostu yz. Symbol mnożenia "×" zazwyczaj nie jest używany, ponieważ zbytnio przypomina literę x, która jest często używana jako zmienna. Ponadto, przy mnożeniu większego wyrażenia można użyć nawiasów: y (z+1).

Kiedy mnożymy liczbę i literę w algebrze, piszemy liczbę przed literą: 5 × y = 5y. Gdy liczbą jest 1, to nie zapisuje się 1, ponieważ 1-krotność dowolnej liczby jest tą liczbą (1 × y = y), a więc nie jest ona potrzebna.

Na marginesie, nie trzeba używać liter x lub y w algebrze. Zmienne są tylko symbolami, które oznaczają jakąś nieznaną liczbę lub wartość, więc możesz użyć dowolnej zmiennej. x i y są jednak najbardziej powszechne.

Funkcje i wykresy

Ważną częścią algebry jest badanie funkcji, ponieważ funkcje często pojawiają się w równaniach, które staramy się rozwiązać. Funkcja jest jak maszyna, do której można włożyć liczbę (lub liczby) i wyprowadzić pewną liczbę (lub liczby) z niej. Kiedy używamy funkcji, wykresy mogą być potężnymi narzędziami pomagającymi nam w badaniu rozwiązań równań.

Wykres jest obrazem, który pokazuje wszystkie wartości zmiennych, które sprawiają, że równanie lub nierówność są prawdziwe. Zazwyczaj jest to łatwe do wykonania, gdy istnieje tylko jedna lub dwie zmienne. Wykres jest często linią, a jeśli linia nie wygina się lub nie idzie prosto w górę i w dół, można to opisać podstawowym wzorem y = mx + b. Zmienna b jest pojęciem y wykresu (gdzie linia przecina oś pionową), a m jest nachyleniem lub stromością linii. Wzór ten odnosi się do współrzędnych wykresu, gdzie każdy punkt na tej linii jest zapisany (x, y).

W niektórych problemach matematycznych, takich jak równanie dla linii, może być więcej niż jedna zmienna (w tym przypadku x i y). Aby znaleźć punkty na linii, jedna zmienna jest zmieniana. Zmienna, która jest zmieniana, jest nazywana "niezależną" zmienną. Następnie wykonuje się matematykę, aby utworzyć liczbę. Utworzona liczba jest nazywana zmienną "zależną". Przez większość czasu niezależna zmienna jest zapisywana jako x a zmienna zależna jako y, na przykład w y = 3x + 1. Często umieszcza się ją na wykresie, używając osi x (idąc w lewo i w prawo) i osi y (idąc w górę i w dół). Można go też zapisać w postaci funkcji: f(x) = 3x + 1. Tak więc w tym przykładzie możemy umieścić 5 dla x i uzyskać y = 16. Wstawienie 2 dla x dawałoby y=7. A 0 dla x otrzymałoby y=1. Byłaby więc linia przechodząca przez punkty (5,16), (2,7) i (0,1), jak widać na wykresie po prawej stronie.

Jeśli x ma moc 1, to jest to linia prosta. Jeżeli jest kwadratowy lub ma jakąś inną moc, to będzie zakrzywiony. Jeśli używa nierówności (< lub > ), to zazwyczaj część wykresu jest zacieniowana, powyżej lub poniżej linii.

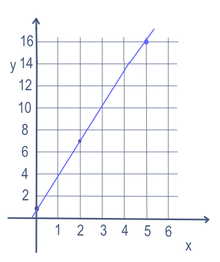
Równanie liniowe dla y=3x+1

Zasady algebry

W algebrze istnieje kilka zasad, które mogą być wykorzystane do dalszego rozumienia równań. Są one nazywane regułami algebry. Chociaż zasady te mogą wydawać się bezsensowne lub oczywiste, to jednak mądrze jest zrozumieć, że właściwości te nie utrzymują się we wszystkich gałęziach matematyki. Dlatego warto wiedzieć, jak te reguły aksjomatyczne są deklarowane, zanim przyjmie się je za oczywiste. Zanim przejdziemy do zasad, zastanówmy się nad dwoma definicjami, które zostaną podane.

1. Naprzeciwko - przeciwieństwem "stylu a" jest "styl -a".
2. Wzajemnie - wzajemnym stylem a jest 1 a stylem a. .

Zasady

Commutative property of addition

Commutative" oznacza, że funkcja ma ten sam wynik, jeśli liczby są zamienione. Innymi słowy, kolejność terminów w równaniu nie ma znaczenia. Gdy operatorem dwóch terminów jest dodanie, zastosowanie ma "komutatywna właściwość dodawania". W terminologii algebraicznej daje to a + b = b + a {\i1}styla a+b=b+a} .

Należy pamiętać, że nie dotyczy to odejmowania! (tj. a - b ≠ b - a {\i1}spis stylistyczny a-b \i0}neq b-a} )

Commutative property of multiplication

Jeżeli operatorem dwóch terminów jest mnożenie, stosuje się "komutatywną właściwość mnożenia". W kategoriach algebraicznych, daje to a ⋅ b = b ⋅ a {\i1}displaystyle a\i0}cdot b=b\i0cdot a} .

Należy pamiętać, że nie dotyczy to podziału! (tzn. a b ≠ b a {\i1} {\i1}displaystyle {\i1}frac {a}{\i1}{\i1} {\i1}neq {\i1}frac {\i1}{a}} kiedy a ≠ b {\i1}splaistyle a\i0}neq b} )

Własność uzupełniająca

Określenie "powiązany" odnosi się do grupowania liczb. Asocjacyjna właściwość dodawania oznacza, że przy dodawaniu trzech lub więcej terminów, nie ma znaczenia, w jaki sposób terminy te są grupowane. Algebraicznie, daje to a + ( b + c ) = ( a + b ) + c {\i1}wyraźny styl a+(b+c)=(a+b)+c} . Należy pamiętać, że nie ma to znaczenia dla odejmowania, np. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\i1} {\i1} styropian 1=0-(0-1)\neq (0-0)-1=-1} (patrz właściwość dystrybucyjna).

Właściwość kojarzona z rozmnażaniem

Asocjacyjna właściwość mnożenia oznacza, że przy mnożeniu trzech lub więcej terminów, nie ma znaczenia, w jaki sposób terminy te są zgrupowane. Algebraicznie, daje to ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\i0}wyraźny styl a \i0}cdot (b\i0cdot c)=(a\i0cdot b)\i0cdot c) . Należy pamiętać, że nie dotyczy to podziału, np. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\i1} {\i1}styl 2=1/(1/2)\i0}neq (1/1)/2=1/2} .

Własność dystrybucyjna

Właściwość rozdzielająca mówi, że mnożenie liczby przez inny termin może być rozdzielone. Na przykład: a ⋅ ( b + c ) = a b + a c {\i1}displaystyle a\i0}cdot (b+c)=ab+ac} . (Nie należy tego mylić z właściwościami kojarzącymi! Na przykład a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\i1}displaystyle a \i0}cdot (b+c)\i0}neq (a\i0cdot b)+c} .) .

Dodatkowa właściwość tożsamościowa

Tożsamość" odnosi się do własności liczby, która jest jej równa. Innymi słowy, istnieje operacja dwóch liczb, tak że równa się ona zmiennej sumy. Właściwość "Identyfikacja dodatku" określa, że suma dowolnej liczby, a 0 jest tą liczbą: a + 0 = a {\i1}styla a+0=a} . To samo odnosi się do odejmowania: a - 0 = a {\i1}stylu a-0=a} .

Tożsamość multiplikatywna własność

Mnożnikowa właściwość identyfikacyjna stwierdza, że iloczyn dowolnej liczby i 1 jest tą liczbą: a ⋅ 1 = a {\i1}styl a {\i0}cdot 1=a} . To samo odnosi się do podziału: a 1 = a {\i1}stylu {\i1}frac {a}{\i1}=a} .

Dodatkowa właściwość odwrotna

Odwrotna właściwość dodatku jest nieco odwrotna od właściwości identyczności dodatku. Gdy operacja jest sumą liczby i jej przeciwieństwem, a jest równa 0, to operacja ta jest ważną operacją algebraiczną. Algebraicznie, stwierdza ona, co następuje: a - a = 0 {\i0} . Dodatkową odwrotnością 1 jest (-1).

Odwrotna właściwość mnożnikowa

Odwrotna właściwość mnożnikowa oznacza, że gdy operacja jest iloczynem liczby i jej wzajemności, a równa jest 1, operacja ta jest ważną operacją algebraiczną. Algebraicznie, stwierdza ona, co następuje: a = 1 {\i1}. Odwrotność mnożnikowa 2 wynosi 1/2.

Zaawansowana Algebra

Oprócz "algebry elementarnej", czyli podstawowej, istnieją zaawansowane formy algebry, nauczane w szkołach wyższych i na uniwersytetach, takie jak algebra abstrakcyjna, algebra liniowa i algebra uniwersalna. Obejmuje to sposób użycia macierzy do rozwiązywania wielu równań liniowych jednocześnie. Algebra abstrakcyjna jest badaniem rzeczy, które znajdują się w równaniach, wykraczającym poza liczby i bardziej abstrakcyjnym z grupami liczb.

Wiele problemów matematycznych dotyczy fizyki i inżynierii. W wielu z tych problemów fizyki czas jest zmienną. Czas używa litery t. Użycie podstawowych pojęć w algebrze może pomóc zredukować problem matematyczny do jego najprostszej formy, ułatwiając rozwiązywanie trudnych problemów. Energia to e, siła to f, masa to m, przyspieszenie to a, a prędkość światła to czasami c. Jest to używane w niektórych słynnych równaniach, takich jak f = ma i e=mc^2 (chociaż bardziej złożona matematyka poza algebrą była potrzebna, aby wymyślić to ostatnie równanie).

Powiązane strony

• Lista tematów matematycznych
• Kolejność operacji
• Parabola
• System Algebry Komputerowej