Algebra elementarna
Algebra elementarna jest najbardziej podstawową formą algebry nauczaną przez uczniów. Często jest to jeden z kolejnych obszarów matematyki nauczanych dla uczniów po arytmetyce. Podczas gdy w arytmetyce występują tylko liczby i operatory jak +, -, × i ÷; w algebrze zmienne (jak a, x, y) oznaczają liczby. Jest to użyteczne, bo:
- Pozwala on ludziom rozwiązywać problemy z "nieznanymi" numerami. Oznacza to poznawanie równań i sposobów ich rozwiązywania (np. "znajdź liczbę x gdzie 3 x + 1 = 10 {\i1}
").
- Pozwala to na uogólnienie reguł z arytmetyki. Podczas gdy niektórzy uczniowie rozumieją, że 3 + 4 = 4 + 3 {\i1}Styl 3+4=4+3}
Pomaga to udowodnić, że a + b = b + a {\i1}styl a+b=b+a}
dla wszystkich a i b. To czyni algebrę dobrym krokiem do nauki abstrakcji (uczenie się ogólnych idei z wielu przykładów).
- Pomaga ludziom zrozumieć i stworzyć funkcjonalne relacje (czasami nazywane również przyczyną i skutkiem). Przykładem tego jest "jeśli sprzeda się x biletów, to zysk wyniesie 3 x - 10 {\i0}
dolarów".
Te trzy są głównymi nurtami elementarnej algebry. Algebra elementarna jest często wykorzystywana w wielu innych dziedzinach, takich jak nauka, biznes i budownictwo. Algebra abstrakcyjna, znacznie bardziej zaawansowany temat, jest na ogół nauczana pod koniec studiów.
Proste problemy z algebrą
Jeśli jakieś równanie ma tylko jedną nieznaną liczbę, to czasami jest łatwe do rozwiązania. Nieznana liczba nazywana jest "x":
2 x + 4 = 12. Styl 2x+4=12.\N,}
Aby rozwiązać proste równanie z jedną nieznaną kwotą dodać, odjąć, pomnożyć lub podzielić obie strony równania przez tę samą liczbę w celu umieszczenia nieznanej kwoty, x, na jednej stronie równania. Gdy x samo znajdzie się po jednej stronie równania, użyj arytmetyki, aby określić kwotę po drugiej stronie równania. Na przykład, poprzez odjęcie 4 z obu stron powyższego równania:
2 x + 4 - 4 = 12 - 4 {\i1}styk 2x+4-4=12-4\i0},}
Robi się:
2 x = 8 {\i1}Styl 2x=8},}
Podzielenie obu stron przez 2:
2 x 2 = 8 2 {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}-{\i1}
Robi się:
x = 4. {\i1}Styl stylistyczny x=4.\i0}
To może pomóc myśleć o tym równaniu jako o huśtawce lub równowadze, co robisz z jedną stroną, musisz zrobić z drugą, a głównym celem jest uzyskanie x samemu.
Definicje
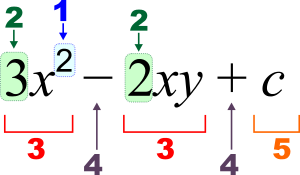
3 x 2 - 2 x y + c {\i1} styropian 3x^{2}-2xy+c}
1 : Wykładnik (moc), 2 : Współczynnik, 3 : termin, 4 : operator, 5 : stała, x , y {\i1} 
Pytania i odpowiedzi
P: Co to jest algebra podstawowa?
O: Algebra podstawowa jest najbardziej podstawową formą algebry nauczaną przez studentów. Zazwyczaj następuje po arytmetyce i polega na używaniu zmiennych (takich jak a, x, y) do oznaczania liczb w równaniach.
P: Jakie są niektóre zastosowania algebry podstawowej?
O: Podstawowa algebra może być wykorzystywana do rozwiązywania problemów dotyczących nieznanych liczb, uogólniania reguł arytmetyki, rozumienia i tworzenia zależności funkcyjnych i jest często stosowana w wielu innych dziedzinach, takich jak nauka, biznes i budownictwo.
P: W jaki sposób algebra podstawowa pomaga ludziom zrozumieć abstrakcyjne pojęcia?
O: Algebra podstawowa pomaga ludziom nauczyć się ogólnych pojęć na wielu przykładach, udowadniając, że a+b=b+a dla wszystkich a i b. Pozwala to lepiej zrozumieć pojęcia abstrakcyjne.
P: Czy algebra abstrakcyjna jest bardziej zaawansowana niż algebra podstawowa?
O: Tak, algebra abstrakcyjna jest zazwyczaj nauczana pod koniec studiów i jest znacznie bardziej zaawansowana niż algebra podstawowa.
P: Jakiego rodzaju równań dotyczy algebra podstawowa?
O: Algebra podstawowa obejmuje równania ze zmiennymi (takimi jak a, x, y) oznaczającymi liczby oraz operatory takie jak +,-,× i ÷.
3x+1=10 {przykład 3x+1=10}
P: Jak zrozumienie algebry podstawowej może pomóc w nauce innych przedmiotów?
O: Zrozumienie elementarnej algebry może pomóc w innych przedmiotach, takich jak nauka, biznes czy budownictwo, ponieważ pozwala rozwiązywać problemy dotyczące nieznanych liczb i tworzyć związki funkcyjne między różnymi zmiennymi.
Przeszukaj encyklopedię




