Nierówność
Nierówność jest wtedy, gdy jeden obiekt jest:
- mniejsza od drugiej ( a < b {\i1} oznacza
, że a jest mniejsza od b)
- większy od drugiego ( a > b {\i1} oznacza
, że a jest większy od b)
- nie mniejsza niż druga ( a ≥ b {\i0}
oznacza, że a jest nie mniejsza niż b, to znaczy, że jest albo większa, albo równa b)
- nie większy od drugiego ( a ≤ b {\i0}
oznacza, że a nie jest większy od b, lub jest mniejszy lub równy b)
Nierówność jest czasami używana do określenia stwierdzenia, że jedno wyrażenie jest mniejsze, większe, nie mniejsze lub nie większe od drugiego.
Praca z nierównościami
Nierówność w matematyce jest wtedy, gdy dwa rozwiązania lub odpowiedzi są porównywane o więcej lub mniej niż. To jest, gdy dwa lub wiele rozwiązań są porównywane nie jest równa. Rozwiązanie nierówności oznacza znalezienie jej rozwiązania. Kiedy zastępujesz liczbę zmienną i stwierdzenie to jest prawdziwe, to jest to rozwiązanie. Kiedy zastępujesz liczbę zmienną, a zdanie nie jest prawdziwe, to liczba nie jest rozwiązaniem dla tego zdania.
Nierówność to znalezienie rozwiązania dla danej zmiennej. Jest to znalezienie względnej kolejności zestawu. Nierówność ma wiele rozwiązań, ale trzeba znaleźć prawdziwe rozwiązania. Nierówność to rozwiązywanie prawdziwych liczb. Prawidłowy sposób odczytywania nierówności jest od lewej do prawej, tak jak w przypadku innych równań, ale jedyną różnicą jest to, że mają one różne zasady dla każdego równania.
Na przykład, x+4>12, gdzie x jest liczbą rzeczywistą. Po pierwsze, osoba musi znaleźć x i musi wiedzieć, czy jest to rozwiązanie. Odpowiedzią będzie x>8 i jest to prawdziwe stwierdzenie. Wyrażenie to dotyczy położenia x w obrębie zbioru liczb rzeczywistych. Linia liczb jest jednym ze sposobów na pokazanie położenia względem wszystkich innych liczb rzeczywistych. (Patrz rysunek Nierówność 1)
.jpg)
Nierówność 1 Jest to rozwiązanie dla równania x+4>12
Różne rodzaje nierówności
Istnieje pięć różnych rodzajów nierówności:
- Pierwszą z nich są nierówności liniowe, które są nierównościami różnicującymi wyrażenia o wartości mniejszej lub równej, mniejszej lub większej lub równej większej niż. Jeśli zastąpimy nierówność równą relacją, to wynik będzie równaniem liniowym.
- Drugi to kombinacje nierówności, które mają zaspokoić nierówności, musisz mieć liczbę w zestawach rozwiązań, tak aby liczby zaspokajające nierówności były wartościami w skrzyżowaniu dwóch zestawów rozwiązań.
- Trzecia to nierówności obejmujące wartości bezwzględne, co oznacza, że wartości te można przeformułować na kombinacje nierówności, które będą obejmowały wartości bezwzględne.
- Czwarty nazywany jest wielomianem nierówności oznacza, że jest on ciągły, to znaczy, że jego wykresy nie mają żadnych skoków ani przerw.
- I wreszcie, co nie mniej ważne, są to racjonalne nierówności, co oznacza, że jest to forma jednego z wielomianów podzielona przez wielomian. Innymi słowy, wykresy funkcji racjonalnych nie mają żadnych przerw ani nie reprezentują zer mianownika.
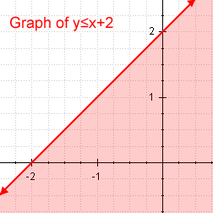
Nierówność liniowa Przykład nierówności liniowej
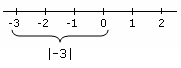
wartość bezwzględna Przykład, który pokazuje wartość bezwzględną
Cztery sposoby na rozwiązanie problemu nierówności
Istnieją cztery sposoby na rozwiązanie równań kwadratowych:
- Zasada numer jeden polega na dodaniu lub odjęciu tej samej liczby po obu stronach.
- Zasada numer dwa polega na tym, że trzeba przesunąć boki i zmienić położenie znaku nierówności.
- Zasada numer trzy polega na tym, że musisz się mnożyć.
- Zasada numer cztery polega na podzieleniu tej samej liczby dodatniej lub ujemnej na obie strony. Ale można ich używać tylko w przypadku łatwych problemów z nierównością.
Ponadto podejmie dwa kroki w celu rozwiązania problemu nierówności. Pierwszy z nich polega na uproszczeniu stosowania zasady wzajemnego dodawania lub odejmowania. Drugi polega na większym uproszczeniu poprzez zastosowanie wzajemności mnożenia lub dzielenia. Kiedy mnożysz lub dzielisz nierówność przez liczbę ujemną, pamiętaj, żeby odwrócić symbol nierówności.

Przykład dodawania nierówności.

przykład mnożenia się nierówności
Przykłady rozwiązywania nierówności
Nierówność to matematyczne stwierdzenie, które wyjaśnia, że te dwie wartości nie są równe i różne. Równanie ab oznacza, że a nie jest równe b. Nierówność jest taka sama z każdym równaniem, ale jedyna różnica polega na tym, że nierówności nie używają znaku równości zamiast symboli. Nierówność b>a oznacza, że b jest większe niż a. Ograniczenia prędkości, znak, a inni używają nierówności do ich wyrażenia.
Przy rozwiązywaniu nierówności osoba musi mieć prawdziwe oświadczenie. Kiedy dzielisz lub mnożysz nierówność z liczbą ujemną po obu stronach, stwierdzenie jest fałszywe. Aby stwierdzenie było poprawne z liczbą ujemną, musisz odwrócić symbol, aby to stwierdzenie było poprawne. Kiedy liczba jest liczbą dodatnią, nie musisz odwracać symbolu. Nierówność polega na składaniu prawdziwego oświadczenia.
Na przykład, zacznij od prawdziwego stwierdzenia -6y<-12. Gdy obie strony są podzielone przez -6, wynikiem będzie y< 2. W tym stwierdzeniu symbol musi być odwrócony, aby mieć prawdziwe stwierdzenie, y>2 jest poprawną odpowiedzią. W linii liczbowej (patrz rys. Inequality 2), zamknięte zacienione koło wskazuje, że jest ono zawarte w zestawie rozwiązań. Otwarte koło wskazuje, że nie jest ono zawarte w zestawie rozwiązań.
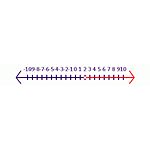
Nierówność 2 Rozwiązanie dla równania -6y<-12
Powiązane strony
- Równość (matematyka)
- Równanie
Pytania i odpowiedzi
P: Co oznacza "a < b"?
A: To znaczy, że a jest mniejsze niż b.
P: Co oznacza "a > b"?
A: To znaczy, że a jest większe niż b.
P: Co oznacza "a ≥ b"?
A: To znaczy, że a nie jest mniejsze od b, to znaczy, że jest albo większe, albo równe b.
P: Co oznacza "a ≤ b"?
A: To znaczy, że a nie jest większe od b, albo jest mniejsze lub równe b.
P: Jak można wykorzystać nierówności w matematyce?
O: Nierówności można użyć do nazwania stwierdzenia, że jedno wyrażenie jest mniejsze, większe, nie mniejsze lub nie większe od drugiego.
Przeszukaj encyklopedię