Fraktal

Przykłady

Istnieje wiele rodzajów fraktali, wykonanych w bardzo różnorodny sposób. Jednym z przykładów jest trójkąt Sierpińskiego, gdzie wewnątrz dużego trójkąta znajduje się nieskończona liczba małych trójkątów. Innym przykładem jest zbiór Mandelbrota, nazwany tak na cześć Benoît Mandelbrota. Trójkąt Sierpińskiego jest skonstruowany przy użyciu wzorów, ale zbiór Mandelbrota jest oparty na równaniu.

Istnieje również wiele naturalnych przykładów fraktali w przyrodzie, w tym drzewa, płatki śniegu, niektóre warzywa i linie brzegowe.

Krzywa Kocha

Krzywa Kocha jest prostym przykładem fraktala. Najpierw zacznij od części linii prostej - zwanej odcinkiem linii prostej. Potnij tę linię na 3 kawałki tej samej wielkości. Pozbądź się środka tych kawałków i włóż do nich górną część trójkąta o bokach tej samej długości, co wycięty kawałek. Mamy teraz 4 odcinki linii, które dotykają się na końcach. Możemy teraz zrobić to, co właśnie zrobiliśmy z pierwszym segmentem dla każdego z 4 bitów. Możemy teraz zrobić to samo ponownie i ponownie do wszystkich bitów, które kończą się z. Teraz robimy to w nieskończoność i patrzymy na to, co otrzymujemy.

Długość krzywej Kocha jest nieskończona, a powierzchnia krzywej Kocha jest równa zero. Jest to dość dziwne. Odcinek linii (o wymiarze 1) może mieć długość 1, ale jego pole wynosi 0. Kwadrat o długości 1 i szerokości 1 (o wymiarze 2) będzie miał pole 1 i długość nieskończoności.

Wymiar podobieństwa

Tak więc, Krzywa Kocha wydaje się być większa niż coś o wymiarze 1, i mniejsza niż coś o wymiarze 2. Ideą wymiaru podobieństwa jest podanie wymiaru, który daje lepsze wyobrażenie o długości lub obszarze dla fraktali. Tak więc, dla krzywej Kocha, chcemy wymiar pomiędzy 1 i 2.

Krzywą Kocha można pociąć na cztery części, z których każda ma rozmiar 1 3 {frac {1}{3}}} wielkości oryginału. Liczbę kawałków, na które można pociąć fraktal nazywamy N {{displaystyle N}} , a różnicę rozmiarów B {{displaystyle B}} . Podstawiamy je do równania:

log N - log B {{displaystyle {{frac {{log N}{-log B}}}

Gdzie log {displaystyle \log } jest logarytmem liczby. Liczba ta jest wymiarem Hausdorffa fraktala. W krzywej Kocha jest to log 4 - log 1 3 = 1.2619... {displaystyle {frac {log 4}{-log {1}{3}}}}=1.2619... } tak jak chcieliśmy.

Krzywa Kocha jest jednym z najprostszych kształtów fraktalnych, a więc jej wymiar jest łatwy do obliczenia. Jej wymiar podobieństwa i wymiar Hausdorffa są takie same. Nie jest to prawdą dla bardziej złożonych fraktali.

Koch płatek śniegu

Płatek śniegu Kocha (lub gwiazda Kocha) jest taki sam jak krzywa Kocha, z tą różnicą, że zaczyna się od trójkąta równobocznego zamiast odcinka linii.

Jak zrobić krzywą Kocha

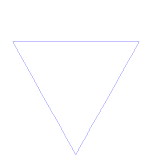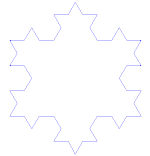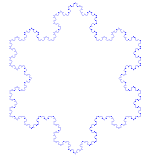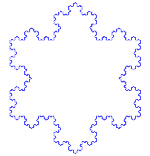
Korzysta z

Fraktale mają wiele zastosowań np. w biologii (płuca, nerki, zmienność rytmu serca, itp...), w trzęsieniach ziemi, w finansach, gdzie są związane z tzw. rozkładami ciężkiego ogona oraz w fizyce. To wskazuje, że fraktale powinny być badane, aby zrozumieć, dlaczego fraktale są tak częste w przyrodzie.

Niektóre fraktale istnieją tylko z powodów artystycznych, ale inne są bardzo użyteczne. Fraktale są bardzo efektywnymi kształtami dla anten radiowych i są używane w chipach komputerowych, aby efektywnie połączyć wszystkie komponenty. Również linie brzegowe mogą być postrzegane jako fraktale.