Wymiar (matematyka)
Wymiary są sposobem, w jaki widzimy, mierzymy i doświadczamy naszego świata. Poprzez używanie w górę i w dół, od prawej do lewej, od tyłu do przodu, gorąco i zimno, jak ciężkie i jak długo, a także bardziej zaawansowane pojęcia z matematyki i fizyki. Jednym ze sposobów zdefiniowania wymiaru jest spojrzenie na stopnie swobody lub na sposób, w jaki obiekt może poruszać się w określonej przestrzeni. Istnieją różne koncepcje lub sposoby użycia terminu "wymiar", istnieją też różne definicje. Nie istnieje żadna definicja, która spełniałaby wszystkie te pojęcia.
W przestrzeni wektorowej, (wektor jest otwartą linią końcową) wymiar jest równy kardynalności lub liczbie kierunków wektorów lub linii. Jest on również równy liczbie największej grupy kierunków linii prostych w tej przestrzeni. Obiekty "normalne" w życiu codziennym są określone przez trzy wymiary, które zwykle nazywane są długością, szerokością i głębokością. Matematycy nazywają to pojęcie przestrzenią euklidesową.
Wymiary mogą być również wykorzystywane do pomiaru pozycji. Odległość do pozycji od miejsca startu może być mierzona w kierunku długości, szerokości i wysokości. Odległości te są miarą pozycji.
Czasami czwarty wymiar (4D), czas, jest używany do pokazania pozycji zdarzenia w czasie i przestrzeni.
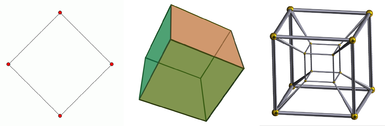
Od lewej do prawej, kwadrat, kostka i tesserakt. Kwadrat jest obiektem dwuwymiarowym, sześcian jest obiektem trójwymiarowym, a tesserakta jest obiektem czterowymiarowym. Obiekt 1-wymiarowy jest tylko linią. Projekcja sześcianu jest podawana, ponieważ jest on oglądany na ekranie dwuwymiarowym. To samo dotyczy tesseraktytu, który dodatkowo może być wyświetlany jako projekcja nawet w przestrzeni trójwymiarowej.

Schemat pierwszych czterech wymiarów przestrzennych.
Inne wymiary
We współczesnej nauce, ludzie używają innych wymiarów. Wymiary takie jak temperatura i waga mogą być wykorzystane do pokazania pozycji czegoś w mniej prostych miejscach. Naukowcy badają te wymiary za pomocą analizy wymiarowej.
Matematycy również używają wymiarów. W matematyce wymiary są bardziej ogólne. Wymiary w matematyce mogą nie mierzyć rzeczy w świecie. Zasady robienia arytmetyki z wymiarami w matematyce mogą być inne niż zwykłe zasady arytmetyczne.
Wymiary i wektory
Wektory służą do wskazywania odległości i kierunków. Wektory są często używane w inżynierii i naukach ścisłych, a czasami w matematyce.
Wektor to lista liczb. Dla każdego wymiaru jest jedna liczba. Istnieją reguły arytmetyczne dla wektorów.
Na przykład, jeśli Jane chce znać pozycję Sally, Sally może dać Jane wektor, który pokaże pozycję. Jeśli Jane i Sally są na świecie, istnieją trzy wymiary. Dlatego też, Sally daje Jane listę trzech liczb, aby pokazać jej pozycję. Te trzy liczby we wektorze, który Sally daje Jane, mogą być:
- Sally's distance north of Jane
- Sally's distance east of Jane
- Wysokość Sally nad Jane
Pytania i odpowiedzi
P: Co to jest wymiar?
O: Wymiar to sposób mierzenia, postrzegania i doświadczania świata za pomocą pojęć takich jak góra i dół, prawo do lewo, tył do przodu, ciepło i zimno, jak ciężki i jak długi. Można go również zdefiniować jako stopnie swobody lub sposób, w jaki obiekt może się poruszać w określonej przestrzeni.
P: Jak matematycy definiują przestrzeń euklidesową?
O: Matematycy definiują przestrzeń euklidesową jako określoną przez trzy wymiary, które zwykle nazywane są długością, szerokością i głębokością.
P: Jaka jest liczba wektorów w przestrzeni wektorowej?
O: Liczba wektorów w przestrzeni wektorowej jest równa kardynalności (lub liczbie wektorów) jej zbioru podstawowego.
P: Ile wymiarów stosuje się do pomiaru położenia?
O: Do pomiaru pozycji używa się trzech wymiarów (długość, szerokość i wysokość). W niektórych przypadkach można zastosować czwarty wymiar (4D) - czas - aby pokazać położenie zdarzenia w czasie i przestrzeni.
P: Co oznacza dim(V)?
O: Dim(V) oznacza wymiar V, który jest równy kardynalności (lub liczbie wektorów) jego zbioru podstawowego lub równy liczbie kierunków linii prostej, które posiada.
P: Czy istnieje jedna definicja, która spełnia wszystkie pojęcia związane z wymiarami?
O: Nie, nie ma jednej definicji, która spełniałaby wszystkie pojęcia związane z wymiarami.
Przeszukaj encyklopedię