Suwak logarytmiczny

Podstawowe pojęcia

W najbardziej podstawowej formie suwak wykorzystuje dwie skale logarytmiczne, które umożliwiają szybkie mnożenie i dzielenie liczb. Te wspólne operacje mogą być czasochłonne i podatne na błędy, gdy są wykonywane na papierze. Bardziej złożone suwaki pozwalają na wykonywanie innych obliczeń, takich jak pierwiastki kwadratowe, wykładniki, logarytmy i funkcje trygonometryczne.

Obliczenia matematyczne wykonywane są poprzez wyrównanie znaku na przesuwanym pasku centralnym z jednym z pasków stałych. Można wtedy obserwować względne położenie innych znaków. Liczby wyrównane ze znakami dają przybliżoną wartość produktu, iloraz lub inny obliczony wynik.

Użytkownik określa lokalizację kropki dziesiętnej w wyniku, na podstawie oszacowania mentalnego. Notacja naukowa jest używana do śledzenia kropki dziesiętnej w bardziej formalnych obliczeniach. Etapy dodawania i odejmowania w obliczeniach są zazwyczaj wykonywane mentalnie lub na papierze, a nie na suwaku.

Większość suwaków ma trzy liniowe pasy o tej samej długości. Listwy te są ułożone równolegle i zsynchronizowane w taki sposób, że środkowa listwa może być przesuwana wzdłużnie w stosunku do dwóch pozostałych. Zewnętrzne dwa paski są zamocowane tak, aby ich względne położenie nie ulegało zmianie.

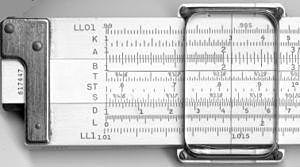
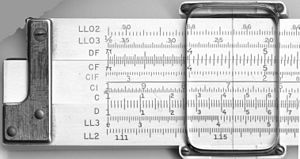
Niektóre suwaki (modele "duplex") posiadają podziałki po obu stronach reguły i suwaka, inne po jednej stronie paska zewnętrznego i obu stronach suwaka, jeszcze inne tylko po jednej stronie (reguły "simplex"). Kursor suwakowy z pionową linią wyrównania służy do znajdowania odpowiednich punktów na wagach, które nie znajdują się obok siebie lub, w modelach "duplex", znajdują się po drugiej stronie reguły. Kursor może również zapisać wynik pośredni na dowolnej ze skal.

Kursor na suwaku

Użycie suwaka logarytmicznego do obliczeń

Mnożenie

Logarytm przekształca operacje mnożenia i dzielenia na dodawanie i odejmowanie zgodnie z zasadami log ( x y ) = log ( x ) + log ( y ) {\i0}log(xy)=log(x)+\i0}log(y)} i log ( x / y ) = log ( x ) - log ( y ) {\i0}log(x/y)=\i0}log(x)-log(y)} . Przesuwając górną skalę w prawo o odległość loga ( x ) {\i1} - log(x)} dopasowując początek górnej skali do etykiety x (styropianx) na dole, wyrównuje każdą liczbę y (styropian y). na pozycji log ( y ) {\i1}w górnej skali, z numerem na pozycji log ( x ) + log ( y ) {\i1}w dolnej skali {\i1}w logu ( x ) + log(y)}. Ponieważ log ( x ) + log ( y ) = log ( x y ) {\i1}log(x)+log(y)=log(xy)} ta pozycja na dolnej skali daje x y {\i1}wyraźny styl xy {y:i}produkt x {y:i}i y {y:i}stylistylu y. . . Na przykład, aby obliczyć 3*2, 1 na górnej skali jest przesuwany do 2 na dolnej skali. Odpowiedź, 6, jest odczytywana z dolnej skali, gdzie 3 jest na górnej skali. Generalnie, 1 na górze przesuwa się na współczynnik na dole, a odpowiedź jest odczytywana na dole, gdzie drugi współczynnik znajduje się na górze.

Operacje mogą być wykonywane "poza skalą"; na przykład, na powyższym schemacie widać, że suwak nie umieścił 7 na górnej skali powyżej żadnej liczby na skali dolnej, a więc nie daje żadnej odpowiedzi dla 2×7. W takich przypadkach użytkownik może przesunąć górną skalę w lewo, aż jego prawy indeks będzie się zgadzał z 2, skutecznie mnożąc ją przez 0,2 zamiast przez 2, jak na rysunku poniżej:

Tutaj użytkownik suwmiarki musi pamiętać o odpowiednim ustawieniu kropki dziesiętnej, aby skorygować ostateczną odpowiedź. Chcieliśmy znaleźć 2×7, ale zamiast tego obliczyliśmy 0,2×7=1,4. Tak więc prawdziwa odpowiedź to nie 1,4, ale 14. Zresetowanie slajdu nie jest jedynym sposobem radzenia sobie z mnożnikami, które dawałyby wyniki poza skalą, np. 2×7; niektóre inne metody są:

• (1) Stosować podwójne skale A i B.
• (2) Użyć złożonej wagi. W tym przykładzie, ustaw lewą 1 z C naprzeciwko 2 z D. Przesuń kursor na 7 na CF i odczytaj wynik z DF.
• (3) Stosować odwróconą skalę CI. Ustawić 7 na skali CI powyżej 2 na skali D, a następnie odczytać wynik na skali D, poniżej 1 na skali CI. Ponieważ 1 występuje w dwóch miejscach na skali CI, jedno z nich będzie zawsze na skali.
• (4) Należy stosować zarówno skalę CI odwróconą, jak i skalę C. Ustawić w linii 2 CI z 1 D i odczytać wynik z D, poniżej 7 na skali C.

Metoda 1 jest łatwa do zrozumienia, ale wiąże się z utratą precyzji. Metoda 3 ma tę zaletę, że obejmuje tylko dwie skale.

Oddział

Ilustracja poniżej przedstawia obliczenie 5,5/2. 2 na górnej skali umieszczone są nad 5,5 na dolnej skali. 1 na górnej skali znajduje się nad ilorazem, 2,75. Istnieje więcej niż jedna metoda dzielenia, ale przedstawiona metoda ma tę zaletę, że ostateczny wynik nie może być poza skalą, ponieważ można użyć 1 na każdym końcu.

Inne operacje

Poza skalami logarytmicznymi, niektóre suwaki posiadają inne funkcje matematyczne zakodowane na innych skalach pomocniczych. Najbardziej popularne były skale trygonometryczna, zwykle sinusoidalna i styczna, logarytm wspólny (log10) (do przyjmowania logu wartości na skali mnożnikowej), logarytm naturalny (ln) i wykładnicza (^ex). Niektóre zasady obejmują skalę pitagorejską, do rysowania boków trójkątów, oraz skalę do rysowania kół. Inne zawierają skale do obliczania funkcji hiperbolicznych. Na zasadach liniowych skale i ich oznaczenia są wysoce znormalizowane, przy czym zmienność występuje zwykle tylko w odniesieniu do tego, które skale są uwzględnione i w jakiej kolejności:

A, B	dwie dekady skali logarytmicznej, służącej do wyszukiwania pierwiastków kwadratowych i kwadratów liczb
C, D	jednokrotna skala logarytmiczna
K	trzydekadowa skala logarytmiczna, służąca do wyszukiwania korzeni sześcianów i kostek liczb
CF, DF	"zagięte" wersje wag C i D, które zaczynają się od π, a nie od jedności; są one wygodne w dwóch przypadkach. Po pierwsze, gdy użytkownik zgadnie, że produkt będzie miał blisko 10, ale nie jest pewien, czy będzie to nieco mniej czy nieco więcej niż 10, złożone wagi unikają możliwości zejścia z tej skali. Po drugie, czyniąc początek π zamiast pierwiastka kwadratowego z 10, upraszcza się mnożenie lub dzielenie przez π (co jest powszechne w nauce i formułach inżynieryjnych).
CI, DI, DIF	"Odwrócona" skala, biegnąca od prawej do lewej, służąca do uproszczenia kroków 1/x.
S	używany do znajdowania sine i cosinusów w skali D
T	używane do znajdowania stycznych i kootangensów na wagach D i DI
ST, SRT	stosowany do sinusów i stycznych o małych kątach i stopniowej konwersji promieniowania
L	skalę liniową, stosowaną wraz ze skalami C i D do odnajdywania logarytmów bazowych 10 i mocy 10
LLn	zestaw wag logarytmicznych, służących do wyszukiwania logarytmów i wykładników liczb
Ln	skalę liniową, stosowaną wraz ze skalami C i D do wyszukiwania logarytmów naturalnych (bazowych e) oraz e x {\i1} styropianu e^{x}}.

 

Waga z przodu i z tyłu suwmiarki K&E 4081-3.

Suwak binarny wyprodukowany przez Gilsona w 1931 r. spełniał funkcję dodawania i odejmowania ograniczoną do ułamków.

Korzenie i moce

Istnieją skale jedno- i dwupoziomowe (C i D), dwu- i trzypoziomowe (A i B) oraz potrójne (K). Aby obliczyć x 2 {\i1}styk x^{2} na przykład zlokalizować x na skali D i odczytać jego kwadrat na skali A. Odwrócenie tego procesu pozwala odnaleźć pierwiastki kwadratowe, i podobnie dla mocy 3, 1/3, 2/3 i 3/2. Należy zachować ostrożność, gdy podstawa, x, znajduje się w więcej niż jednym miejscu na swojej skali. Na przykład, na skali A znajdują się dwie dziewiątki; aby znaleźć pierwiastek kwadratowy z dziewięciu, należy użyć pierwszego; drugi daje pierwiastek kwadratowy z 90.

W przypadku problemów z x y {\i1}wyglądem stylistycznym x^{y}, użyj skali LL. Kiedy jest kilka skal LL, użyj tej z x na niej. Najpierw wyrównaj najbardziej lewą 1 na skali C z x na skali LL. Następnie, znajdź y na skali C i zejdź do skali LL z x na niej. Skala ta wskaże odpowiedź. Jeśli y jest "poza skalą", znajdź x y / 2 {\i1}styk stylistyczny x^{y/2}} i kwadratuj go używając skal A i B, jak opisano powyżej.

Trigonometria

Skale S, T i ST są używane do funkcji trygonometrycznych i wielokrotności funkcji wyzwalania, dla kątów w stopniach. Wiele suwaków ma swoje skale S, T i ST oznaczone stopniami i minutami. Tak zwane modele dekitrygowe używają zamiast tego ułamków dziesiętnych stopni.

Logarytmy i wykładniki

Baza-10 logarytmów i wykładników znajduje się przy użyciu skali L, która jest liniowa. Niektóre suwaki posiadają skalę Ln, która jest dla podstawy e.

Waga Ln została wymyślona przez ucznia 11 klasy, Stephena B. Cohena, w 1958 roku. Pierwotnym zamiarem było umożliwienie użytkownikowi wybrania wykładnika x (w zakresie od 0 do 2,3) na skali Ln i odczytania ^{ex na} skali C (lub D) oraz ^e-x na skali CI (lub DI). Pickett, Inc. otrzymał wyłączne prawa do tej skali. Później wynalazca stworzył zestaw "znaków" na skali Ln w celu rozszerzenia zakresu poza limit 2,3, ale Pickett nigdy nie włączył tych znaków do żadnego ze swoich suwaków. ^[]

Dodawanie i odejmowanie

Reguły suwakowe nie są zazwyczaj stosowane do dodawania i odejmowania, niemniej jednak można to zrobić przy użyciu dwóch różnych technik.

Pierwsza metoda dodawania i odejmowania na skali C i D (lub dowolnej porównywalnej) wymaga przeliczenia problemu na jeden z podziałów. W przypadku dodawania, iloraz dwóch zmiennych plus jednokrotna wartość dzielnika jest równy ich sumie:

x + y = ( x y + 1 ) y {\i1} y {\i1}styl x+y= {\i1}lewa({\i1}frac {\i1}{y}{\i1}prawda)y}

W przypadku odejmowania, iloraz dwóch zmiennych minus jednokrotność dzielnika jest równy ich różnicy:

x - y = ( x y - 1 ) y {\i1} y {\i1}styl x-y= {\i1}lewa(\i0}frac {\i1}{y}{\i1}prawda?}

Metoda ta jest podobna do techniki dodawania/odejmowania stosowanej w szybkich układach elektronicznych z systemem liczb logarytmicznych w specjalistycznych aplikacjach komputerowych, takich jak superkomputer Gravity Pipe (GRAPE) i ukryte modele Markova.

Druga metoda wykorzystuje przesuwną liniową skalę L dostępną w niektórych modelach. Dodawanie i odejmowanie odbywa się poprzez przesuwanie kursora w lewo (dla odejmowania) lub w prawo (dla dodawania), a następnie powrót slajdu do 0 w celu odczytania wyniku.

Konstrukcja fizyczna

Standardowe zasady liniowe

Długość suwaka podana jest w postaci nominalnej długości skali. Skale w najbardziej popularnych modelach "10-calowych" mają w rzeczywistości 25 cm długości, ponieważ zostały wykonane zgodnie z normami metrycznymi, chociaż niektóre zasady oferują nieznacznie wydłużone skale w celu ułatwienia manipulacji w przypadku przepełnienia wyniku. Kieszonkowe reguły mają zazwyczaj długość 5 cali. Modele o długości kilku metrów zostały sprzedane do powieszenia w klasach w celach dydaktycznych. [1]

Zazwyczaj podziały oznaczają skalę z dokładnością do dwóch znaczących cyfr, a użytkownik szacuje trzecią cyfrę. Niektóre wysokiej klasy suwaki są wyposażone w kursory powiększające, które sprawiają, że oznaczenia są lepiej widoczne. Takie kursory mogą skutecznie podwoić dokładność odczytów, pozwalając na zastosowanie suwaka 10-calowego, jak i 20-calowego.

Opracowano różne inne udogodnienia. Skale trygonometryczne są czasami podwójnie oznakowane, w kolorze czarnym i czerwonym, z kątami uzupełniającymi, tzw. styl "Darmstadt". Dupleksowe suwaki często powielają niektóre z wag z tyłu. Wagi są często "dzielone" w celu uzyskania większej dokładności.

Specjalistyczne prowadnice zostały wynalezione dla różnych form inżynierii, biznesu i bankowości. Często miały one wspólne obliczenia wyrażone bezpośrednio w specjalnych skalach, np. obliczenia kredytowe, optymalne ilości zakupów lub konkretne równania inżynieryjne. Na przykład, firma Fisher Controls rozprowadzała suwak dostosowany do potrzeb klienta, dostosowany do rozwiązywania równań stosowanych przy doborze odpowiedniego rozmiaru przemysłowych zaworów regulujących przepływ. ^[]

Suwaki okrągłe

Okrągłe suwaki występują w dwóch podstawowych typach, jeden z dwoma kursorami (po lewej), a drugi z ruchomym dyskiem i jednym kursorem (po prawej). Wersje z dwoma kursorami wykonują mnożenie i dzielenie, utrzymując stały kąt pomiędzy kursorami podczas ich obracania wokół tarczy. Wersja z pojedynczym kursorem działa bardziej jak standardowy suwak, dzięki odpowiedniemu ustawieniu skali.

Podstawową zaletą suwaka okrągłego jest to, że najdłuższy wymiar narzędzia został zmniejszony o współczynnik około 3 (tj. o π). Na przykład, skala zewnętrzna okrągłego 10 cm miałaby maksymalną dokładność równą 30 cm zwykłego suwaka. Suwaki okrągłe również eliminują obliczenia "poza skalą", ponieważ skale zostały zaprojektowane tak, aby "owijały się"; nigdy nie trzeba ich przekierowywać, gdy wyniki są bliskie 1,0 - reguła jest zawsze na skali. Jednak w przypadku niecyklicznych, nie-spiralnych skal, takich jak S, T i LL, długość skali jest skrócona, aby zrobić miejsce na marginesy końcowe.

Suwaki okrągłe są bardziej wytrzymałe mechanicznie i płynnie poruszają się, ale ich dokładność ustawienia w skali jest wrażliwa na centrowanie centralnego przegubu; minuta 0,1 mm od środka przegubu może spowodować najgorszy błąd ustawienia w skali 0,2 mm. Sworzeń zapobiega jednak zarysowaniom powierzchni czołowej i kursorów. Skale o najwyższej dokładności są umieszczone na pierścieniach zewnętrznych. Zamiast skal "dzielonych", wysokiej klasy skale okrągłe wykorzystują skale spiralne do bardziej złożonych operacji, takich jak skale log-of-log. Jedna ośmiocalowa, wysokiej klasy skala okrągła posiada 50-calową, spiralną skalę log log-log.

Głównymi wadami suwaków okrągłych są trudności z lokalizacją cyfr wzdłuż obracającej się tarczy oraz ograniczona liczba skal. Kolejną wadą suwaków okrągłych jest to, że mniej ważne skale znajdują się bliżej środka i mają mniejszą precyzję. Większość uczniów nauczyła się korzystać z suwaków liniowych i nie znalazła powodu do ich zmiany.

Jedną z prowadnic pozostającą w codziennym użyciu na całym świecie jest E6B. Jest to okrągły suwak stworzony po raz pierwszy w latach trzydziestych XX wieku dla pilotów samolotów, aby pomóc w martwym liczeniu. Za pomocą skali wydrukowanej na ramie pomaga również w różnych zadaniach, takich jak przeliczanie czasu, odległości, prędkości i wartości temperatury, błędów kompasu oraz obliczanie zużycia paliwa. Tak zwane "koło modlitewne" jest nadal dostępne w sklepach lotniczych i pozostaje szeroko stosowane. Podczas gdy GPS zmniejszył wykorzystanie martwego liczenia do nawigacji lotniczej, a ręczne kalkulatory przejęły wiele z jego funkcji, E6B pozostaje szeroko stosowany jako urządzenie podstawowe lub zapasowe, a większość szkół lotniczych wymaga od swoich uczniów pewnego stopnia jego opanowania.

W 1952 roku szwajcarska firma zegarmistrzowska Breitling wprowadziła na rynek zegarek na rękę pilota ze zintegrowaną okrągłą prowadnicą suwakową specjalizującą się w obliczeniach lotniczych: Breitling Navitimer. Reguła kołowa Navitimer, określana przez Breitlinga jako "komputer nawigacyjny", zawierała funkcje dotyczące prędkości lotu, prędkości/czasu wznoszenia/zniżania, czasu lotu, odległości i zużycia paliwa, a także funkcje przeliczania ilości paliwa na milę morską i galon-litr.

Materiały

Tradycyjnie prowadnice wykonane były z twardego drewna, takiego jak mahoń czy bukszpan z kursorami ze szkła i metalu. Co najmniej jeden precyzyjny instrument był wykonany ze stali.

W 1895 roku japońska firma Hemmi rozpoczęła produkcję suwaków z bambusa, których zaletą było to, że były stabilne wymiarowo, mocne i naturalnie samosmarujące. Te suwaki bambusowe zostały wprowadzone w Szwecji we wrześniu 1933 roku [2], a prawdopodobnie nieco wcześniej w Niemczech. Wagi były wykonane z celuloidu lub tworzywa sztucznego. Później suwaki wykonywano z plastiku lub aluminium malowanego plastikiem. Później kursorem były akryle lub poliwęglany ślizgowe na łożyskach teflonowych.

Wszystkie suwaki premium posiadały wygrawerowane numery i podziałki, a następnie wypełnione farbą lub inną żywicą. Pomalowane lub nadrukowane suwaki były postrzegane jako gorsze, ponieważ oznaczenia mogły się ścierać. Niemniej jednak Pickett, prawdopodobnie najbardziej znana amerykańska firma produkująca suwaki, wykonała wszystkie drukowane wagi. Wysokiej klasy suwaki zawierały sprytne zaczepy, aby nie rozpadły się przypadkowo, oraz zderzaki chroniące wagę i kursor przed przetarciem o blaty. Zalecaną metodą czyszczenia wygrawerowanych oznaczeń jest lekkie szorowanie wełną stalową. W przypadku malowanych suwaków i słabego serca należy używać rozcieńczonego, dostępnego w handlu płynu do mycia okien i miękkiej szmatki.

Suwak pikietujący z dwoma kursorami. (średnica 4,25 cala/10,9 cm) Rewers posiada dodatkową skalę i jeden kursor.


Prosta, okrągła prowadnica suwakowa, wyprodukowana przez Concise Co., Ltd., Tokio, Japonia, posiadająca tylko skale odwrotną, kwadratową i sześcienną. Na odwrocie znajduje się poręczna lista 38 metrycznych/imperialnych współczynników przeliczeniowych.


Breitling Navitimer zegarek na rękę z okrągłym suwakiem

Historia

Suwak logarytmiczny został wynaleziony około 1620-1630 roku, wkrótce po opublikowaniu przez Johna Napiera koncepcji logarytmu. Edmund Gunter z Oxfordu opracował urządzenie obliczeniowe z pojedynczą skalą logarytmiczną, które przy pomocy dodatkowych narzędzi pomiarowych można było mnożyć i dzielić. Pierwszy opis tej skali został opublikowany w Paryżu w 1624 roku przez Edmunda Wingate'a (ok. 1593-1656), angielskiego matematyka, w książce zatytułowanej "L'usage de la reigle de proportion en l'arithmetique & geometrie". Książka ta zawiera z jednej strony podwójną skalę, która jest skalą logarytmiczną, a z drugiej tabelaryczną. W 1630 roku William Oughtred z Cambridge wynalazł suwak okrągły, a w 1632 roku połączył dwie reguły Guntera, trzymane razem z rękami, aby stworzyć urządzenie, które jest rozpoznawalne jako nowoczesny suwak. Podobnie jak współczesny mu Isaac Newton z Cambridge, Oughtred uczył swoich pomysłów prywatnie swoich uczniów, ale z opóźnieniem je opublikował, i podobnie jak Newton, zaangażował się w kontrowersje o pierwszeństwo, ze swoim niegdyś uczniem Richardem Delamainem i uprzednimi roszczeniami Wingate'a. W 1632 roku połączył dwie zasady Guntera, trzymane razem z rękami, aby stworzyć urządzenie, które będzie rozpoznawalne jako nowoczesny suwak. Pomysły Oughtreda zostały podane do publicznej wiadomości dopiero w publikacjach jego ucznia Williama Forstera w latach 1632 i 1653.

W 1677 roku Henry Coggeshall stworzył dwumetrową regułę składaną do miarki drewnianej, zwaną suwakiem Coggeshall. Jego projekt i zastosowanie dla tego narzędzia dało suwakowi cel poza dociekaniami matematycznymi.

W 1722 r. Warner wprowadził dwu- i trzyetapowe skale, a w 1755 r. Everard zawarł w nich skalę odwróconą; suwak zawierający wszystkie te skale jest zazwyczaj znany jako reguła "polifazowa".

W 1815 roku Peter Roget wynalazł suwak logarytmu, który zawierał skalę przedstawiającą logarytm logarytmu. Pozwoliło to użytkownikowi na bezpośrednie wykonywanie obliczeń z użyciem pierwiastków i wykładników. Było to szczególnie przydatne w przypadku mocy cząstkowych.

Nowoczesna forma

Bardziej nowoczesna forma została stworzona w 1859 roku przez porucznika artylerii francuskiej Amédée Mannheim, "który miał szczęście, że jego władza została wykonana przez firmę o reputacji narodowej i przyjęta przez artylerię francuską". Mniej więcej w tym samym czasie, gdy inżynieria stała się uznaną działalnością zawodową, suwaki zaczęły być szeroko stosowane w Europie. W Stanach Zjednoczonych stały się one powszechne dopiero w 1881 roku, kiedy to Edwin Thacher wprowadził tam regułę cylindryczną. Reguła podwójna została wynaleziona przez Williama Coxa w 1891 r. i została wyprodukowana przez Keuffela i Esser Co. z Nowego Jorku.

Prace astronomiczne wymagały również precyzyjnych obliczeń, a w XIX wieku w Niemczech w jednym z obserwatoriów stosowano stalową prowadnicę o długości około 2 metrów. Miała ona przymocowany mikroskop, co dawało jej dokładność do sześciu miejsc po przecinku.

W czasie II wojny światowej bombardatorzy i nawigatorzy, którzy wymagali szybkich obliczeń, często korzystali ze specjalistycznych suwaków. Jedno z biur Marynarki Wojennej Stanów Zjednoczonych zaprojektowało ogólny suwak "chassis" z aluminiową obudową i plastikowym kursorem, w którym można było umieścić karty celuloidowe (drukowane po obu stronach) do specjalnych obliczeń. Proces ten został wynaleziony w celu obliczenia zasięgu, zużycia paliwa i wysokości dla samolotów, a następnie dostosowany do wielu innych celów.

W latach 50. i 60. suwak był symbolem zawodu inżyniera (tak jak stetoskop symbolizuje zawód lekarza). ^[] Niemiecki naukowiec od rakiet Wernher von Braun przywiózł ze sobą dwa zabytkowe suwaki Nestlera z lat 30. ubiegłego wieku, gdy po II wojnie światowej przeniósł się do Stanów Zjednoczonych, aby pracować nad amerykańskim programem kosmicznym. Przez całe życie nie używał żadnych innych kieszonkowych urządzeń obliczeniowych; suwaki doskonale służyły mu do szybkiego szacowania parametrów konstrukcyjnych rakiet i innych danych. Aluminiowe suwaki marki Pickett były przewożone na pięciu misjach kosmicznych Apollo, w tym na Księżyc, zgodnie z reklamą na pudełkach suwaków Picketta N600 [3].

Niektórzy studenci inżynierii i inżynierowie nosili dziesięciocalowe suwaki w kaburach pasowych i nawet w połowie lat 70-tych był to powszechny widok na kampusach. Studenci mogli również stosować zasadę dziesięciu lub dwudziestu cali do precyzyjnej pracy w domu lub biurze, nosząc przy sobie suwak kieszonkowy o pięciu calach.

W 2004 roku badacze edukacji David B. Sher i Dean C. Nataro opracowali nowy typ reguły suwakowej opartej na protezie szkieletowej, algorytm szybkiego przetwarzania produktów, który wyprzedza logarytmy. Niewiele jednak było praktycznego zainteresowania konstrukcją takiego algorytmu poza pierwotnym prototypem. [4]

Spadek

Znaczenie suwaka zaczęło maleć, ponieważ komputery elektroniczne, nowy, ale bardzo rzadki zasób w latach pięćdziesiątych XX wieku, stały się powszechnie dostępne dla pracowników technicznych w latach sześćdziesiątych. Wprowadzenie Fortranu w 1957 r. sprawiło, że komputery stały się praktyczne w rozwiązywaniu problemów matematycznych o niewielkich rozmiarach. IBM wprowadził serię bardziej przystępnych cenowo komputerów: IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) skierowanych na rynek nauki i inżynierii. Język programowania John Kemeny'ego BASIC (1964) ułatwił uczniom korzystanie z komputerów. Minikomputer DEC PDP-8 został wprowadzony na rynek w 1965 roku.

Komputery zmieniły również charakter obliczeń. Dzięki suwakom duży nacisk położono na pracę z algebrą w celu uzyskania wyrażeń w najbardziej obliczalnej formie. Użytkownicy suwaków po prostu przybliżali lub upuszczali małe terminy, aby uprościć obliczenia. Fortran pozwalał na wpisywanie skomplikowanych formuł z podręczników bez wysiłku przeformułowywania. Integracja numeryczna była często łatwiejsza niż szukanie rozwiązań w formie zamkniętej dla trudnych problemów. Młody inżynier proszący o czas komputerowy, aby rozwiązać problem, który mógł być zrobiony kilkoma machnięciami na suwaku, stał się żartobliwym banałem. W wielu centrach komputerowych na ścianie wisiał obramowany suwak z adnotacją "W razie potrzeby potłucz szkło".

Kolejnym krokiem w kierunku zastąpienia prowadnic suwakowych elektroniką było opracowanie elektronicznych kalkulatorów do zastosowań naukowych i inżynieryjnych. Pierwsze z nich to wprowadzone w 1965 r. Laboratoria Wang LOCI-2, które wykorzystywały logarytmy do mnożenia i dzielenia oraz wprowadzony w 1968 r. Hewlett-Packard HP-9100. HP-9100 posiadał funkcje trygonometryczne (grzech, cos, opalenizna) oprócz wykładników i logarytmów. Wykorzystywał on algorytm CORDIC (komputer cyfrowy z rotacją współrzędnych), który pozwala na obliczanie funkcji trygonometrycznych przy użyciu tylko operacji przesunięcia i dodawania. Metoda ta ułatwiła rozwój coraz mniejszych kalkulatorów naukowych.

Ostatnim gwoździem do trumny na suwak było uruchomienie kieszonkowych kalkulatorów naukowych, z których pierwszym był Hewlett-Packard HP-35 z 1972 roku. Kalkulatory takie stały się znane jako kalkulatory "suwakowe", ponieważ mogły one pełnić większość lub wszystkie funkcje na suwaku. Za kilkaset dolarów, nawet to było uważane za kosztowne dla większości studentów. Podczas gdy profesjonalne suwaki również mogły być dość drogie, drogie apteki często sprzedawały podstawowe plastikowe modele za mniej niż 20 dolarów. Ale do 1975 roku podstawowe czterofunkcyjne kalkulatory elektroniczne można było kupić za mniej niż 50 dolarów. W 1976 r. TI-30 zaoferował kalkulator naukowy za mniej niż 25 dolarów. Po tym czasie rynek suwaków szybko wyschł, gdy małe kalkulatory naukowe stały się przystępne cenowo.

William Oughtred (1575-1660), wynalazca suwaka okrągłego


Inżynier używający suwaka. Uwaga na kalkulator mechaniczny w tle.


TI-30

Zalety

• Suwak suwak ma tendencję do modulowania błędu "fałszywej precyzji" i znaczenia. Typowa precyzja, jaką dysponuje użytkownik suwaka, to około trzech miejsc precyzji. Jest to zgodne z większością danych dostępnych do wprowadzenia do formuł inżynieryjnych. W przypadku zastosowania nowoczesnego kalkulatora kieszonkowego, dokładność może być wyświetlana z dokładnością do siedmiu lub więcej miejsc po przecinku, podczas gdy w rzeczywistości wyniki nigdy nie mogą być bardziej dokładne niż dostępne dane wejściowe.
• Suwak logarytmiczny wymaga ciągłego szacowania rzędu wielkości wyników. Na suwaku 1,5 × 30 (co równa się 45) pokaże ten sam wynik co 1 500 000 × 0,03 (co równa się 45 000). Do inżyniera należy ciągłe ustalanie zasadności wyników, co może zostać utracone w przypadku nieostrożnego wprowadzania liczb do programu komputerowego lub kalkulatora.
• Podczas wykonywania sekwencji mnożenia lub dzielenia przez tę samą liczbę, odpowiedź może być często określona poprzez zwykłe spojrzenie na suwak, bez jakiejkolwiek manipulacji. Może to być szczególnie przydatne przy obliczaniu procentów, np. dla wyników testu, lub przy porównywaniu cen, np. w dolarach za kilogram. Wielokrotne obliczenia prędkości i odległości w czasie mogą być wykonywane bez użycia rąk za pomocą suwaka.
• Suwak nie zależy od elektryczności.
• Suwak logarytmiczny jest technologią łatwą do powielenia. Z danego przykładu suwak może być zbudowany przez kompetentnego rzemieślnika z podstawowych materiałów z wykorzystaniem nieprzemysłowych procesów.
• Reguły suwakowe są wysoce ustandaryzowane, więc nie ma potrzeby uwalniania niczego przy przechodzeniu na inną regułę.
• Reguły suwakowe są uniwersalne i mogą być stosowane w sytuacjach i środowiskach, w których użytkownik ludzki może mieć ograniczoną zręczność (na przykład ze względu na konieczność użycia rękawic ochronnych). I odwrotnie, w takich sytuacjach obsługa kalkulatora może być trudna - suwak jest mało prawdopodobne, aby spowodował błąd podobny do tego wynikającego z błędnego naciśnięcia niewłaściwego przycisku na kalkulatorze.
• Suwaki mogą być wykonane z kartonu lub papieru. Wiele darmowych wykresów lub specjalistycznych urządzeń obliczeniowych wykonanych z kartonu to w rzeczywistości specjalistyczne suwaki liniowe lub kołowe.

Jedną z zalet stosowania suwmiarki wraz z kalkulatorem elektronicznym jest to, że ważne obliczenia można sprawdzić wykonując je na obu instrumentach; ponieważ te dwa instrumenty są tak różne, że istnieje małe prawdopodobieństwo popełnienia tego samego błędu dwa razy.

Wady

• Błędy mogą wynikać z mechanicznej niedokładności.
• Obliczenia przy użyciu suwaka są mało precyzyjne ze względu na ich analogowe wejścia i wyjścia. I odwrotnie, dzięki dyskretnym wejściom numerycznym i zmiennoprzecinkowym operacjom elektronicznym, nawet skromne nowoczesne kalkulatory mają rozdzielczość wyjściową wynoszącą co najmniej sześć znaczących liczb.

Powiązane strony

• Abacus
• Logarytm