Teoria chaosu — co to jest? Definicja, efekt motyla i przykłady
Teoria chaosu — zrozum, jak niewielkie zmiany (efekt motyla) wpływają na systemy. Definicja, przykłady i zastosowania — czy rzeczywiście wszystko da się przewidzieć?
Teoria chaosu jest działem matematyki (i jednocześnie interdyscyplinarną częścią nauk przyrodniczych), który bada zachowanie pewnych układów dynamicznych bardzo wrażliwych na warunki początkowe. Oznacza to, że bardzo mała zmiana na początku obserwowanego procesu może po pewnym czasie spowodować zupełnie inną ewolucję tego układu.
Co to znaczy „chaotyczny”?
W codziennym użyciu słowo „chaos” oznacza bałagan lub przypadkowość, ale w sensie naukowym układ chaotyczny jest zazwyczaj deterministyczny — jego przyszłość jest w pełni określona przez równania rządzące systemem — i jednocześnie praktycznie nieprzewidywalny z powodu ekstremalnej wrażliwości na warunki początkowe. Innymi słowy:
- Deterministyczny — brak losowości w równaniach (przynajmniej w modelu),
- Wrażliwy na warunki początkowe — bardzo mała różnica na początku rośnie z czasem,
- Składniki strukturalne — chaotyczne trajektorie często układają się na tzw. dziwnych atraktorach o fraktalnej strukturze.
Efekt motyla
Pojęcie efektu motyla ilustruje właśnie tę wrażliwość: mała zmiana (np. trzepot skrzydeł motyla) teoretycznie może wpłynąć na rozwój zjawisk atmosferycznych i w długim okresie przyczynić się do znaczącej zmiany pogody. W praktyce efekt ten oznacza, że nawet bardzo dokładne pomiary nie pozwalają na dowolnie długie prognozy — drobne błędy pomiarowe lub nieznane wpływy rosną z upływem czasu i ograniczają horyzont przewidywalności. Dlatego nawet duże komputery i zaawansowane modele meteorologiczne przewidują pogodę tylko z ograniczoną dokładnością na kilka dni lub tygodni.
Charakterystyczne cechy i narzędzia analizy
- Współczynniki Lyapunova — mierzą, jak szybko od siebie oddalają się dwie bardzo bliskie trajektorie; dodatni współczynnik wskazuje na chaos.
- Przestrzeń fazowa — reprezentacja stanu układu; chaotyczne trajektorie często tworzą złożone struktury (atraktory).
- Diagramy bifurkacji — pokazują, jak zmiana parametru modelu prowadzi do przejścia od zachowań regularnych do chaotycznych.
- Fraktale i dziwne atraktory — geometryczne struktury wyłaniające się w analizie długoterminowych trajektorii (np. atraktor Lorentza).
Przykłady układów chaotycznych
- Model Lorentza — prosty model atmosferyczny, od którego wywodzi się historia efektu motyla i którego atraktor jest jednym z najbardziej znanych przykładów.
- Drgający podwójny wahadłowiec — proste urządzenie mechaniczne o bardzo złożonym, chaotycznym ruchu przy pewnych parametrach.
- Mapa logistyczna — dyskretny model populacji, który przy zmianie współczynnika rozrodczości przechodzi od okresowych cykli do chaosu.
- Pogoda i klimat — układy atmosferyczne wykazują chaotyczne cechy, co tłumaczy ograniczenia dokładnych prognoz.
- Układy biologiczne i medyczne — rytmy serca, oscylacje neuronów; chaos bywa związany zarówno ze zdrowiem (elastyczność systemu), jak i zaburzeniami (np. arytmie).
Chaos a przypadkowość
Warto rozróżnić chaos deterministyczny od prawdziwej losowości. Chaotyczny układ jest zdeterminowany przez swoje równania, ale z punktu widzenia obserwatora, który nie zna idealnie warunków początkowych, jego zachowanie może wyglądać na losowe. To właśnie dlatego systemy chaotyczne potrafią wyglądać „przypadkowo”, chociaż nie są nimi w sensie matematycznym.
Zastosowania i konsekwencje praktyczne
- Prognozowanie — w meteorologii i naukach o Ziemi chaos określa horyzont przewidywalności.
- Modelowanie biologiczne i ekologiczne — wyjaśnianie nieregularnych fluktuacji populacji czy dynamiki epidemii.
- Inżynieria i sterowanie — wykorzystanie teorii chaosu do projektowania systemów odpornych na zakłócenia albo do sterowania nimi.
- Kryptografia i generatory liczb losowych — niektóre chaotyczne układy są wykorzystywane do uzyskania złożonych, trudnych do przewidzenia sygnałów.
Kwantowa teoria chaosu
Jak wspomniano w artykule, kwantowa teoria chaosu to obszar badań łączący teorię chaosu z fizyką kwantową. Bada ona, jak klasyczne cechy chaosu (np. wrażliwość na warunki początkowe) przejawiają się w układach rządzonych zasadami mechaniki kwantowej, gdzie pojęcia trajektorii czy przestrzeni fazowej mają inny sens. To wciąż intensywnie rozwijana dziedzina nauki.
Podsumowanie
Główna idea teorii chaosu to to, że niewielkie różnice na początku procesu mogą prowadzić do dużych i nieoczekiwanych zmian w dłuższej perspektywie. Teoria ta tłumaczy, dlaczego pewne systemy wydają się nieprzewidywalne mimo determinizmu rządzących nimi równań, i dostarcza narzędzi do ich analizy. Znajomość właściwości układów chaotycznych jest dziś ważna w meteorologii, biologii, inżynierii, ekonomii i wielu innych dziedzinach nauki.
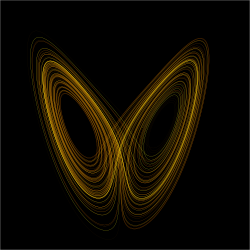
Wykres funkcji chaotycznej zwanej atraktorem Lorenza.

Gdyby te dwa połączone wahadła rozpoczęły pracę w pozycji, która byłaby choć trochę inna, szara linia wyglądałaby zupełnie inaczej.
Przykłady
Jako przykład weźmy wahadło, które jest zamocowane w pewnym punkcie i kołysze się swobodnie. Podłączenie drugiego wahadła do pierwszego sprawi, że układ będzie zupełnie inny. Bardzo trudno jest zacząć ponownie w dokładnie tym samym położeniu - zmiana położenia początkowego tak mała, że nawet jej nie widać, może szybko spowodować, że wahania wahadła staną się inne niż były wcześniej.
Bardzo ważną częścią badań nad teorią chaosu jest badanie funkcji matematycznych, które znane są jako fraktale. Funkcje fraktalne działają jak systemy chaotyczne: niewielka zmiana wartości początkowych może zmienić wartość funkcji w sposób, który wygląda na przypadkowy. Ze względu na fakt, że są one matematyczne, są łatwe do zbadania.
Powiązane strony
- Funkcja nieciągła
Pytania i odpowiedzi
P: Co to jest teoria chaosu?
O: Teoria chaosu to dziedzina matematyki zajmująca się badaniem systemów, które są bardzo wrażliwe, a mała zmiana w systemie może spowodować, że zachowa się on zupełnie inaczej.
P: Dlaczego nawet duże komputery nie są w stanie dokładnie przewidzieć pogody?
O: Nawet duże komputery nie potrafią przewidzieć pogody, ponieważ pozycja wyjściowa systemu chaotycznego, takiego jak pogoda, jest bardzo wrażliwa na małe zmiany i nawet niewielki błąd lub zmiana może sprawić, że prognoza będzie całkowicie błędna.
P: Co to jest "efekt motyla"?
O: "Efekt motyla" to koncepcja w teorii chaosu, która odnosi się do idei, że nawet małe zmiany, takie jak trzepotanie skrzydeł motyla, mogą mieć duży wpływ na system chaotyczny, taki jak pogoda.
P: Czy istnieją systemy, które mogą wydawać się przypadkowe, ale w rzeczywistości nie są?
O: Tak, teoria chaosu sugeruje, że niektóre systemy lub wzory mogą wydawać się na początku przypadkowe, ale mogą takie nie być, a uważna obserwacja może ujawnić chaotyczne wzory.
P: Jaka jest główna idea teorii chaosu?
O: Główną ideą teorii chaosu jest to, że niewielka różnica w pozycji wyjściowej procesu może spowodować jego znaczącą zmianę w miarę upływu czasu.
P: Co to jest teoria chaosu kwantowego?
O: Teoria chaosu kwantowego to nowa idea w badaniach nad teorią chaosu, która stosuje jej zasady do fizyki kwantowej.
P: Jak bardzo małe zmiany wpływają na systemy chaotyczne?
O: Bardzo małe zmiany w pozycji wyjściowej układu chaotycznego mogą w znacznym stopniu zmienić jego zachowanie w czasie. Dzieje się tak dlatego, że układy chaotyczne są bardzo wrażliwe i małe zmiany mogą prowadzić do znacznych różnic w ich zachowaniu.
Przeszukaj encyklopedię