Mechanika kwantowa
Mechanika kwantowa (QM) opisuje, jak działa Wszechświat na poziomie mniejszym niż atomy. Nazywa się ją również "fizyką kwantową" lub "teorią kwantową". Quantum to łacińskie słowo oznaczające "ile", a mechanika jest dziedziną nauki zajmującą się ruchem. Kwant energii to określona ilość energii, a mechanika kwantowa opisuje, jak ta energia porusza się i oddziałuje na poziomie subatomowym.
Atomy były uważane za najmniejszy budulec materii, ale współczesna nauka wykazała, że istnieją jeszcze mniejsze cząstki, takie jak protony, neutrony i elektrony. QM jest tą częścią fizyki, która opisuje jak działają cząstki tworzące atomy.
QM mówi nam również, jak działają fale elektromagnetyczne (takie jak światło). Znaczna część współczesnej fizyki i chemii może być opisana i zrozumiana przy użyciu matematycznych zasad mechaniki kwantowej.
Matematyka używana do badania cząstek subatomowych i fal elektromagnetycznych jest bardzo skomplikowana, ponieważ zachowują się one w bardzo dziwny sposób.
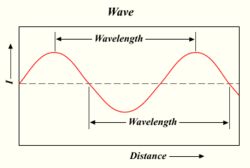
Długość fali świetlnej
Fale i fotony
Fotony są cząsteczkami znacznie mniejszymi niż atomy, protony i elektrony; w rzeczywistości nie mają one żadnej masy. Fotony są jak "paczki" lub pakiety energii. Źródła światła takie jak świece czy lasery wystrzeliwują (lub "emitują") światło w kawałkach zwanych fotonami.
Im więcej fotonów emituje lampa, tym jaśniejsze jest światło. Światło jest formą energii, która zachowuje się jak fale w wodzie lub fale radiowe. Odległość pomiędzy wierzchołkiem jednej fali a wierzchołkiem następnej fali nazywana jest "długością fali". Każdy foton niesie pewną ilość, lub "kwant", energii w zależności od długości fali.
Kolor światła zależy od długości jego fali. Kolor fioletowy (dolny lub najbardziej wewnętrzny kolor tęczy) ma długość fali około 400 nm ("nanometrów"), co odpowiada 0,00004 centymetra lub 0,000016 cala. Fotony o długości fali 10-400 nm nazywane są światłem ultrafioletowym (lub UV). Światło takie nie jest widoczne dla ludzkiego oka. Na drugim końcu spektrum znajduje się światło czerwone o długości fali około 700 nm. Światło podczerwone ma długość od 700 nm do 300 000 nm. Ludzkie oczy również nie są wrażliwe na światło podczerwone.
Długości fal nie zawsze są tak małe. Fale radiowe mają dłuższe fale. Długość fali dla radia FM może wynosić kilka metrów (na przykład stacje nadające na częstotliwości 99,5 FM emitują energię radiową o długości fali około 3 metrów, czyli około 10 stóp). Każdy foton ma pewną ilość energii związaną z długością fali. Im krótsza jest długość fali fotonu, tym większa jest jego energia. Na przykład, foton ultrafioletowy ma większą energię niż foton podczerwony.
Długość fali i częstotliwość (liczba powtórzeń fali w ciągu sekundy) są odwrotnie proporcjonalne, co oznacza, że dłuższa fala będzie miała niższą częstotliwość i odwrotnie. Jeśli kolor światła to podczerwień (o niższej częstotliwości niż światło czerwone), każdy foton może podgrzać to, w co trafi. Tak więc, jeśli silna lampa na podczerwień (lampa grzewcza) jest skierowana na osobę, osoba ta poczuje ciepło, a nawet gorąco, z powodu energii zgromadzonej w wielu fotonach. Powierzchnia lampy na podczerwień może nawet rozgrzać się na tyle, by poparzyć osobę, która może jej dotknąć. Człowiek nie widzi światła podczerwonego, ale może odczuwać promieniowanie w postaci ciepła. Na przykład, osoba przechodząca obok budynku z cegły, który został ogrzany przez słońce, poczuje ciepło z budynku bez konieczności dotykania go.
Matematyczne sformułowania mechaniki kwantowej są abstrakcyjne. Funkcja matematyczna, zwana funkcją falową, dostarcza informacji o amplitudzie prawdopodobieństwa (kwadrat amplitudy prawdopodobieństwa jest prawdopodobieństwem) położenia, pędu i innych właściwości fizycznych cząstki. Wielu wyników mechaniki kwantowej nie da się łatwo zobrazować w kategoriach mechaniki klasycznej.
Światło ultrafioletowe ma wyższą częstotliwość niż światło fioletowe, tak że nie należy nawet do zakresu światła widzialnego. Każdy foton w zakresie ultrafioletowym ma dużą energię, wystarczającą do uszkodzenia komórek skóry i spowodowania oparzenia słonecznego. W rzeczywistości, większość form oparzeń słonecznych nie jest spowodowana ciepłem; są one spowodowane wysoką energią słonecznych promieni UV, które uszkadzają komórki skóry. Jeszcze wyższe częstotliwości światła (lub promieniowania elektromagnetycznego) mogą wnikać głębiej w ciało i powodować jeszcze większe szkody. Promieniowanie rentgenowskie ma tak dużą energię, że może wnikać w głąb ludzkiego ciała i zabijać komórki. Ludzie nie widzą i nie czują światła ultrafioletowego ani promieniowania rentgenowskiego. O tym, że znajdowali się pod działaniem światła o tak wysokiej częstotliwości, mogą się dowiedzieć dopiero po oparzeniu promieniowaniem. W miejscach, gdzie ważne jest zabijanie zarazków, często stosuje się lampy ultrafioletowe do niszczenia bakterii, grzybów itp. Promieniowanie rentgenowskie jest czasami używane do zabijania komórek rakowych.
Mechanika kwantowa zaczęła się, gdy odkryto, że pewna częstotliwość oznacza pewną ilość energii. Energia jest proporcjonalna do częstotliwości (E ∝ f). Im wyższa częstotliwość, tym więcej energii ma foton i tym większe szkody może wyrządzić. Mechanika kwantowa rozwinęła się później do wyjaśnienia wewnętrznej struktury atomów. Mechanika kwantowa wyjaśnia również sposób, w jaki foton może interferować sam ze sobą, a także wiele innych rzeczy, których nie wyobrażano sobie w fizyce klasycznej.

Kolor czarny po lewej stronie to ultrafiolet (wysoka częstotliwość); kolor czarny po prawej stronie to podczerwień (niska częstotliwość).
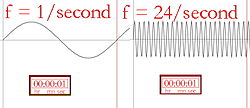
Obrazowy opis częstotliwości
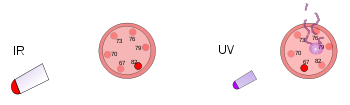
Po lewej stronie, plastikowy termometr znajduje się pod jasną lampą grzewczą. Promieniowanie podczerwone ogrzewa termometr, ale go nie uszkadza. Po prawej stronie, inny plastikowy termometr jest poddany działaniu światła ultrafioletowego o niskim natężeniu. Promieniowanie to uszkadza termometr, ale go nie ogrzewa.
Quantization
Max Planck odkrył związek między częstotliwością i energią. Nikt wcześniej nie przypuszczał, że częstotliwość jest wprost proporcjonalna do energii (oznacza to, że gdy jedna z nich się podwaja, druga również). W tak zwanych jednostkach naturalnych, liczba reprezentująca częstotliwość fotonu reprezentowałaby również jego energię. Równanie brzmiałoby wtedy:
E = f
co oznacza, że energia równa się częstotliwości.
Jednak w sposobie, w jaki rozwijała się fizyka, nie było naturalnego związku pomiędzy jednostkami używanymi do mierzenia energii i jednostkami powszechnie używanymi do mierzenia czasu (a więc i częstotliwości). Tak więc wzór, który Planck opracował, aby liczby się zgadzały, brzmiał następująco:
E = h × f
lub, energia równa się h razy częstotliwość. To h jest liczbą zwaną stałą Plancka od nazwiska jej odkrywcy.
Mechanika kwantowa opiera się na wiedzy, że foton o pewnej częstotliwości oznacza foton o pewnej ilości energii. Poza tą zależnością, określony rodzaj atomu może emitować tylko pewne częstotliwości promieniowania, a więc może też emitować tylko fotony o określonej energii.
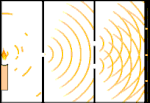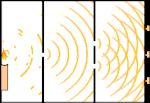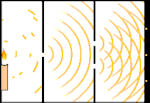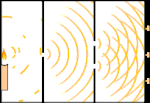
Doświadczenie z podwójną szczeliną: światło przechodzi od źródła światła po lewej stronie do frędzli (zaznaczonych czarną krawędzią) po prawej stronie.
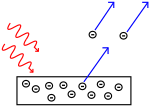
Efekt fotoelektryczny: fotony uderzają w metal i elektrony są odpychane.
Historia
Isaac Newton uważał, że światło składa się z bardzo małych elementów, które obecnie nazywamy cząsteczkami (nazywał je "korpuskułami"). Christiaan Huygens uważał, że światło jest zbudowane z fal. Naukowcy uważali, że dana rzecz nie może być jednocześnie cząstką i falą.
Naukowcy przeprowadzili eksperymenty, aby dowiedzieć się, czy światło jest zbudowane z cząsteczek czy z fal. Okazało się, że obie koncepcje były słuszne - światło było w jakiś sposób zarówno falami, jak i cząstkami. Eksperyment z podwójną szczeliną przeprowadzony przez Thomasa Younga pokazał, że światło musi zachowywać się jak fala. Efekt fotoelektryczny odkryty przez Alberta Einsteina dowiódł, że światło musiało zachowywać się jak cząstki, które niosły ze sobą określone ilości energii, a energie te były związane z ich częstotliwościami. Ten eksperymentalny wynik nazywany jest w mechanice kwantowej "dualizmem fala-cząstka". Później fizycy odkryli, że wszystko zachowuje się zarówno jak fala, jak i jak cząstka, nie tylko światło. Jednak w przypadku dużych obiektów efekt ten jest znacznie mniejszy.
Oto niektórzy z ludzi, którzy odkryli podstawowe elementy mechaniki kwantowej: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann i Richard Feynman. Swoje prace wykonywali w pierwszej połowie XX wieku.

Od lewej do prawej: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Beyond Planck
Wzory i idee mechaniki kwantowej zostały stworzone, aby wyjaśnić światło, które pochodzi z rozżarzonego wodoru. Kwantowa teoria atomu musiała również wyja¶nić, dlaczego elektron pozostaje na swojej orbicie, czego inne koncepcje nie były w stanie wyja¶nić. Ze starszych pomysłów wynikało, że elektron musiałby wpa¶ć do ¶rodka atomu, ponieważ pocz±tkowo był utrzymywany na orbicie przez własn± energię, ale szybko traciłby energię w miarę jak obracałby się po swojej orbicie. (To dlatego, że elektrony i inne naładowane cząstki były znane z emitowania światła i tracenia energii, gdy zmieniały prędkość lub obracały się).
Lampy wodorowe działają jak neony, ale neony mają swoją własną, unikalną grupę kolorów (i częstotliwości) światła. Naukowcy odkryli, że mogą zidentyfikować wszystkie pierwiastki na podstawie kolorów światła, które wytwarzają. Nie mogli tylko dowiedzieć się, jak określane są częstotliwości.
Następnie, szwajcarski matematyk Johann Balmer opracował równanie, które mówiło, jaka będzie λ (lambda, czyli długość fali):
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {displaystyle {lambda =Bleft({frac {n^{2}}{n^{2}-4}}}}right)\quad \quad n=3,4,5,6}
gdzie B jest liczbą, którą Balmer określił jako równą 364,56 nm.
To równanie działało tylko dla światła widzialnego z lampy wodorowej. Jednak później równanie to stało się bardziej ogólne:
1 λ = R ( 1 m 2 - 1 n 2 ), { {displaystyle {{frac {1}{lambda }}=Rleft({{frac {1}{m^{2}}}}-{{frac {1}{n^{2}}}}right),}
gdzie R jest stałą Rydberga, równą 0,0110 nm-1, a n musi być większe od m.
Wstawiając różne liczby dla m i n, łatwo jest przewidzieć częstotliwości dla wielu rodzajów światła (ultrafioletowego, widzialnego i podczerwieni). Aby zobaczyć jak to działa, wejdź na stronę Hyperphysics i zejdź na dół, poza środek strony. (Użyj H = 1 dla wodoru).
W 1908 r. Walter Ritz opracował zasadę kombinacji Ritza, która pokazuje, jak pewne przerwy między częstotliwościami powtarzają się. Okazało się to ważne dla Wernera Heisenberga kilka lat później.
W 1905 r. Albert Einstein wykorzystał ideę Plancka, aby wykazać, że wiązka światła składa się ze strumienia cząstek zwanych fotonami. Energia każdego fotonu zależy od jego częstotliwości. Pomysł Einsteina jest początkiem idei w mechanice kwantowej, że wszystkie cząstki subatomowe, takie jak elektrony, protony, neutrony i inne są jednocześnie falami i cząstkami. (Zobacz zdjęcie atomu z elektronem jako falą w atomie). Doprowadziło to do powstania teorii o cząstkach subatomowych i falach elektromagnetycznych zwanej dualizmem fala-cząstka. Polega ona na tym, że cząstki i fale nie są ani jednym, ani drugim, ale mają pewne właściwości obu.
W 1913 roku Niels Bohr wpadł na pomysł, że elektrony mogą zajmować tylko pewne orbity wokół jądra atomu. Zgodnie z teorią Bohra, liczby m i n w powyższym równaniu mogły reprezentować orbity. Teoria Bohra mówiła, że elektrony mogą zaczynać na jakiejś orbicie m i kończyć na orbicie n, albo elektron może zaczynać na jakiejś orbicie n i kończyć na orbicie m. Jeśli więc foton uderzy w elektron, jego energia zostanie zaabsorbowana, a elektron przeniesie się na wyższą orbitę dzięki tej dodatkowej energii. Zgodnie z teorią Bohra, jeśli elektron spadnie z wyższej orbity na niższą, to będzie musiał oddać energię w postaci fotonu. Energia fotonu będzie równa różnicy energii pomiędzy dwoma orbitami, a energia fotonu sprawia, że ma on określoną częstotliwość i kolor. Teoria Bohra dobrze wyjaśniała wiele aspektów zjawisk subatomowych, ale nie potrafiła odpowiedzieć, dlaczego każdy z kolorów światła wytwarzanego przez świecący wodór (a także przez świecący neon czy jakikolwiek inny pierwiastek) ma swoją własną jasność, a różnice jasności są zawsze takie same dla każdego pierwiastka.
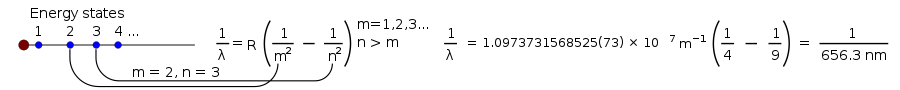
Zanim Niels Bohr przedstawił swoją teorię, większość rzeczy na temat światła wytwarzanego przez lampę wodorową była już znana, ale naukowcy nadal nie potrafili wyjaśnić jasności każdej z linii wytwarzanych przez świecący wodór.
Werner Heisenberg podjął się zadania wyjaśnienia jasności lub "intensywności" każdej linii. Nie mógł użyć żadnej prostej zasady, jak ta, którą wymyślił Balmer. Musiał posłużyć się bardzo trudną matematyką fizyki klasycznej, która oblicza wszystko w kategoriach takich rzeczy jak masa (ciężar) elektronu, ładunek (statyczna siła elektryczna) elektronu i inne maleńkie wielkości. Fizyka klasyczna miała już odpowiedzi na pytanie o jasność pasm kolorów, które wytwarza lampa wodorowa, ale teoria klasyczna mówiła, że powinna być ciągła tęcza, a nie cztery oddzielne pasma kolorów. Wyjaśnienie Heisenberga brzmi następująco:
Istnieje pewne prawo, które mówi, jakie częstotliwości światła będzie wytwarzał świecący wodór. Musi ono przewidywać rozłożone w czasie częstotliwości, gdy elektrony poruszają się pomiędzy orbitami blisko jądra (centrum) atomu, ale musi również przewidywać, że częstotliwości będą się zbliżać i zbliżać do siebie, gdy przyjrzymy się temu, co elektron robi poruszając się pomiędzy orbitami coraz dalej i dalej. Przewiduje również, że różnice intensywno¶ci pomiędzy częstotliwo¶ciami będ± coraz bliższe siebie w miarę oddalania się. Tam, gdzie fizyka klasyczna dawała już właściwe odpowiedzi za pomocą jednego zestawu równań, nowa fizyka musi dawać te same odpowiedzi, ale za pomocą innych równań.
Fizyka klasyczna wykorzystuje metody francuskiego matematyka Fouriera, aby stworzyć matematyczny obraz świata fizycznego, i wykorzystuje kolekcje gładkich krzywych, które łączą się w jedną gładką krzywą, która daje, w tym przypadku, natężenia światła o wszystkich częstotliwościach z pewnego światła. Ale to nie jest w porządku, ponieważ ta gładka krzywa pojawia się tylko przy wyższych częstotliwościach. Przy niższych częstotliwościach, zawsze są pojedyncze punkty i nic nie łączy kropek. Tak więc, aby stworzyć mapę rzeczywistego świata, Heisenberg musiał dokonać dużej zmiany. Musiał zrobić coś, aby wybrać tylko te liczby, które pasowałyby do tego, co widać w naturze. Czasami ludzie mówią, że "zgadywał" te równania, ale on nie zgadywał na ślepo. Znalazł to, czego potrzebował. Liczby, które wyliczył, umieściłyby kropki na wykresie, ale nie byłoby linii narysowanej między kropkami. A robienie jednego "wykresu" składającego się z kropek dla każdego zestawu obliczeń spowodowałoby zmarnowanie mnóstwa papieru i nie przyniosłoby żadnych rezultatów. Heisenberg znalazł sposób, aby efektywnie przewidzieć natężenia dla różnych częstotliwości i zorganizować te informacje w pomocny sposób.
Używając tylko empirycznej reguły podanej powyżej, tej, którą zapoczątkował Balmer, a udoskonalił Rydberg, możemy zobaczyć, jak uzyskać jeden zestaw liczb, który pomógłby Heisenbergowi uzyskać taki obraz, jaki chciał:
Reguła mówi, że kiedy elektron przechodzi z jednej orbity na drugą, to albo zyskuje albo traci energię, w zależności od tego, czy jest coraz dalej od centrum, czy coraz bliżej. Możemy więc umieścić te orbity lub poziomy energetyczne jako nagłówki wzdłuż górnej i bocznej części siatki. Dla historycznych powodów najniższa orbita nazywa się n, a następna orbita na zewnątrz nazywa się n - a, potem przychodzi n - b, i tak dalej. To jest mylące, że używali liczb ujemnych, gdy elektrony faktycznie zyskiwały energię, ale to jest po prostu sposób, w jaki to jest.
Ponieważ reguła Rydberga daje nam częstotliwo¶ć, możemy użyć tej reguły do wprowadzenia liczb w zależno¶ci od tego, dok±d zmierza elektron. Jeżeli elektron zaczyna się w punkcie n i kończy w punkcie n, to tak naprawdę nigdzie się nie udał, więc nie zyskał energii ani jej nie stracił. Zatem częstotliwość wynosi 0. Jeśli elektron zaczyna się na n-a i kończy na n, to znaczy, że spadł z wyższej orbity na niższą. Jeśli tak się stało, to traci on energię, a energia, którą traci, objawia się jako foton. Foton ma pewną ilość energii, e, a ta jest związana z pewną częstotliwością f równaniem e = h f. Wiemy więc, że pewna zmiana orbity wytworzy pewną częstotliwość światła, f. Jeśli elektron zaczyna na n, a kończy na n - a, to znaczy, że przeszedł z niższej orbity na wyższą. Dzieje się to tylko wtedy, gdy foton o pewnej częstotliwości i energii przychodzi z zewnątrz, jest absorbowany przez elektron i daje mu swoją energię, i to właśnie sprawia, że elektron wychodzi na wyższą orbitę. Tak więc, aby wszystko miało sens, zapisujemy tę częstotliwość jako liczbę ujemną. Istniał foton o określonej częstotliwości, a teraz został on zabrany.
Możemy więc stworzyć taką siatkę, gdzie f(a←b) oznacza częstotliwość związaną z przejściem elektronu ze stanu energetycznego (orbity) b do stanu energetycznego a (znowu, sekwencje wyglądają na odwrócone, ale tak właśnie były oryginalnie zapisane):
Siatka f
| Stany elektronowe | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| przejście .... | ..... | ..... | ..... | ..... |
Heisenberg nie stworzył siatki w ten sposób. Po prostu wykonał obliczenia, które pozwoliły mu uzyskać natężenia, których szukał. Ale żeby to zrobić, musiał pomnożyć dwie amplitudy (jak wysoko mierzy fala), aby obliczyć natężenie. (W fizyce klasycznej natężenie równa się amplitudzie podniesionej do kwadratu). Aby rozwiązać ten problem, ułożył dziwnie wyglądające równanie, napisał resztę pracy, wręczył ją swojemu szefowi i pojechał na wakacje. Dr Born spojrzał na swoje zabawne równanie i wydało mu się ono nieco szalone. Musiał się zastanawiać: "Dlaczego Heisenberg dał mi tę dziwną rzecz? Dlaczego on musi to robić w ten sposób?". Potem zdał sobie sprawę, że patrzy na schemat czegoś, co już bardzo dobrze znał. Był przyzwyczajony do nazywania siatki lub tabeli, którą mogliśmy napisać, wykonując, na przykład, całą matematykę dla częstotliwości, macierzą. A dziwne równanie Heisenberga było regułą na mnożenie dwóch z nich razem. Max Born był bardzo, bardzo dobrym matematykiem. Wiedział, że skoro dwie mnożone macierze (siatki) reprezentują różne rzeczy (jak na przykład położenie (x,y,z) i pęd (mv)), to kiedy pomnożysz pierwszą macierz przez drugą, otrzymasz jedną odpowiedź, a kiedy pomnożysz drugą macierz przez pierwszą, otrzymasz inną odpowiedź. Heisenberg, mimo że nie znał się na matematyce macierzowej, już wtedy widział ten problem "różnych odpowiedzi" i to go niepokoiło. Ale dr Born był tak dobrym matematykiem, że zauważył, iż różnica pomiędzy pierwszym i drugim mnożeniem macierzy zawsze będzie dotyczyła stałej Plancka, h, pomnożonej przez pierwiastek kwadratowy z ujemnej jedynki, i. Tak więc w ciągu kilku dni od odkrycia Heisenberga mieli już podstawową matematykę dla tego, co Heisenberg lubił nazywać "zasadą nieokreśloności". Przez "nieokreśloność" Heisenberg rozumiał to, że coś takiego jak elektron jest po prostu nie do spięcia, dopóki nie zostanie spięte. Jest to trochę jak meduza, która zawsze się gniecie i nie może być "w jednym miejscu", chyba że się ją zabije. Później ludzie zaczęli nazywać to "zasadą nieoznaczoności Heisenberga", co sprawiło, że wielu ludzi popełniało błąd myśląc, że elektrony i podobne rzeczy są naprawdę "gdzieś", ale my tylko nie jesteśmy co do tego pewni w naszych własnych umysłach. Ta myśl jest błędna. Nie o tym mówił Heisenberg. Problemy z mierzeniem czegoś są problemem, ale to nie jest problem, o którym mówił Heisenberg.
Idea Heisenberga jest bardzo trudna do uchwycenia, ale możemy ją wyjaśnić na przykładzie. Po pierwsze, zaczniemy nazywać te siatki "macierzami", ponieważ wkrótce będziemy musieli mówić o mnożeniu macierzy.
Załóżmy, że zaczynamy od dwóch rodzajów pomiarów, położenia (q) i pędu (p). W 1925 roku Heisenberg napisał równanie podobne do tego:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {{displaystyle Y(n,n-b)=suma _{a}^{} p(n,n-a)q(n-a,n-b)}. 
Nie wiedział o tym, ale to równanie daje schemat jak napisać dwie macierze (siatki) i jak je mnożyć. Zasady mnożenia jednej macierzy przez drugą są trochę niechlujne, ale oto dwie macierze według wzoru, a następnie ich iloczyn:
Macierz p
| Stany elektronowe | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| przejście .... | ..... | ..... | ..... | ..... |
Macierz q
| Stany elektronowe | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| przejście .... | ..... | ..... | ..... | ..... |
Macierz dla iloczynu powyższych dwóch macierzy, określona odpowiednim równaniem w pracy Heisenberga z 1925 roku, ma postać:
| Stany elektronowe | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Gdzie:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+ .....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+ .....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+ .....
i tak dalej.
Gdyby odwrócić te macierze, otrzymalibyśmy następujące wartości:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-.....b)+
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-.....c)+
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+. .....
i tak dalej.
Zauważ, jak zmiana kolejności mnożenia zmienia liczby, krok po kroku, które są faktycznie mnożone.

Widzialne światło emitowane przez żarzący się wodór. (Długość fali w nanometrach.)
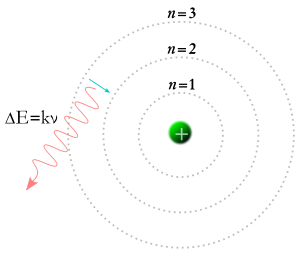
Elektron spada na niższą orbitę i powstaje foton.
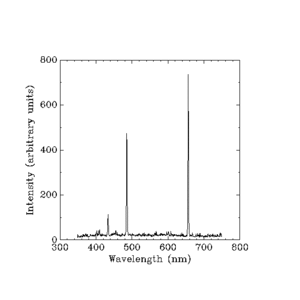
Rozmieszczone natężenia w jednostkach arbitralnych
Poza Heisenbergiem
Praca Wernera Heisenberga zdawała się przełamywać zator. Bardzo szybko pojawiło się wiele innych sposobów wyjaśniania zjawisk przez takich ludzi jak Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli i Erwin Schrödinger. Praca każdego z tych fizyków to osobna historia. Matematyka stosowana przez Heisenberga i wcześniejszych ludzi nie jest bardzo trudna do zrozumienia, ale równania szybko stały się bardzo skomplikowane, gdy fizycy zaczęli bardziej zagłębiać się w świat atomu.
Kolejne tajemnice
We wczesnych dniach mechaniki kwantowej Albert Einstein zasugerował, że gdyby mechanika kwantowa była słuszna, oznaczałoby to, że istnieje "upiorne działanie na odległość". Okazało się, że mechanika kwantowa miała rację i że to, co Einstein wykorzystał jako powód do odrzucenia mechaniki kwantowej, rzeczywiście miało miejsce. Ten rodzaj "upiornego połączenia" pomiędzy pewnymi zdarzeniami kwantowymi jest obecnie nazywany "splątaniem kwantowym".
Kiedy w wyniku eksperymentu dwie rzeczy (fotony, elektrony, itp.) zbliżają się do siebie, muszą mieć wspólny opis w mechanice kwantowej. Kiedy później zostaną rozdzielone, zachowują ten sam opis mechaniki kwantowej lub "stan". Na diagramie jedna cecha (np. spin "w górę") jest narysowana na czerwono, a jej kolega (np. spin "w dół") na niebiesko. Fioletowe pasmo oznacza, że kiedy np. dwa elektrony s± poł±czone razem, to dziel± one obie cechy. Tak więc oba elektrony mogą wykazywać spin w górę lub w dół. Kiedy później zostaną rozdzielone, jeden z nich pozostanie na Ziemi, a drugi poleci na jakąś planetę gwiazdy Alfa Centauri, nadal każdy z nich będzie miał oba spiny. Innymi słowy, każdy z nich może "zdecydować" aby pokazać się jako elektron o spinie w górę lub jako elektron o spinie w dół. Jeśli jednak później ktoś zmierzy ten drugi, musi on "zdecydować" aby pokazać się jako posiadający przeciwny spin.
Einstein argumentował, że na tak wielkiej odległości szaleństwem jest myślenie, że zmuszenie jednego elektronu do pokazania swojego spinu spowoduje, że drugi elektron będzie miał przeciwną charakterystykę. Powiedział, że te dwa elektrony musiały być spin-up lub spin-down przez cały czas, ale mechanika kwantowa nie mogła przewidzieć, jaką cechę miał każdy z elektronów. Niemożność przewidzenia, a jedynie możliwość przyjrzenia się jednemu z nich za pomocą odpowiedniego eksperymentu, oznaczała, że mechanika kwantowa nie mogła wyjaśnić czegoś ważnego. Dlatego, powiedział Einstein, mechanika kwantowa miała w sobie wielką dziurę. Mechanika kwantowa była niekompletna.
Później okazało się, że eksperymenty wykazały, iż to Einstein się mylił.
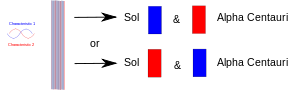
Dwie splątane cząstki zostają rozdzielone: jedna na Ziemi, a druga zabrana na jakąś odległą planetę. Pomiar jednej z nich zmusza ją do "zdecydowania", którą rolę ma przyjąć, a druga musi przyjąć tę drugą rolę, ilekroć (po tym) zostanie zmierzona.
Zasada nieoznaczoności Heisenberga
W 1925 r. Werner Heisenberg opisał zasadę nieoznaczoności, która mówi, że im więcej wiemy o tym, gdzie znajduje się cząstka, tym mniej możemy wiedzieć o tym, jak szybko się porusza i w jakim kierunku. Innymi słowy, im więcej wiemy o prędkości i kierunku czegoś małego, tym mniej możemy wiedzieć o jego położeniu. W takich dyskusjach fizycy zwykle mówią o pędzie, zamiast o prędkości. Moment pędu to po prostu prędkość czegoś w pewnym kierunku razy jego masa.
Zasada nieoznaczoności Heisenberga mówi, że nigdy nie możemy znać zarówno położenia, jak i pędu cząstki. Ponieważ światło jest cząstką o dużej masie, jest używane do pomiaru innych cząstek. Jedynym sposobem jego pomiaru jest odbicie fali świetlnej od cząstki i zarejestrowanie wyników. Jeśli użyjemy wiązki światła o wysokiej energii lub wysokiej częstotliwości, możemy dokładnie określić, gdzie się ona znajduje, ale nie możemy stwierdzić, jak szybko się poruszała. Dzieje się tak, ponieważ foton o wysokiej energii przenosi energię na cząstkę i zmienia jej prędkość. Jeśli użyjemy fotonu o niskiej energii, możemy powiedzieć, jak szybko się porusza, ale nie gdzie się znajduje. Dzieje się tak dlatego, że używamy światła o większej długości fali. Dłuższa fala oznacza, że cząstka może znajdować się w dowolnym miejscu wzdłuż odcinka fali.
Zasada ta mówi również, że istnieje wiele par pomiarów, dla których nie możemy wiedzieć obu o żadnej cząstce (bardzo małej rzeczy), bez względu na to, jak bardzo byśmy się starali. Im więcej dowiemy się o jednej z takich par, tym mniej możemy wiedzieć o drugiej.
Nawet Albert Einstein miał problemy z zaakceptowaniem tak dziwacznej koncepcji i w znanej debacie powiedział: "Bóg nie gra w kości". Na to duński fizyk Niels Bohr słynnie odpowiedział: "Einsteinie, nie mów Bogu, co ma robić".
Zastosowania QM
Elektrony otaczają jądro każdego atomu. Wiązania chemiczne łączą atomy, tworząc cząsteczki. Wiązanie chemiczne łączy dwa atomy, gdy elektrony są dzielone między te atomy. QM jest więc fizyką wiązania chemicznego i chemii. QM pomaga nam zrozumieć, jak powstają cząsteczki i jakie są ich właściwości.
QM może również pomóc nam zrozumieć wielkie rzeczy, takie jak gwiazdy, a nawet cały wszechświat. QM jest bardzo ważną częścią teorii o początku wszechświata zwanej Wielkim Wybuchem.
Wszystko, co jest zbudowane z materii, przyciąga się do innej materii z powodu fundamentalnej siły zwanej grawitacją. Teoria Einsteina, która wyjaśnia grawitację, nazywana jest ogólną teorią względności. Problemem we współczesnej fizyce jest to, że niektóre wnioski z QM wydają się nie zgadzać z ogólną teorią względności.
QM jest tą częścią fizyki, która może wyjaśnić dlaczego cała technologia elektroniczna działa tak jak działa. Tak więc QM wyjaśnia, jak działają komputery, ponieważ komputery są maszynami elektronicznymi. Jednak projektanci wczesnego sprzętu komputerowego z około 1950 lub 1960 roku nie musieli myśleć o QM. Ówcześni konstruktorzy odbiorników radiowych i telewizyjnych również nie myśleli o QM. Jednak projektowanie potężniejszych układów scalonych i technologii pamięci komputerowych ostatnich lat wymaga QM.
QM umożliwił również powstanie takich technologii jak:
Dlaczego QM jest trudna do nauczenia
QM jest trudnym tematem z kilku powodów:
- QM wyja±nia rzeczy w bardzo odmienny sposób od tego, czego uczymy się o ¶wiecie, gdy jeste¶my dziećmi.
- Zrozumienie QM wymaga więcej matematyki ni" algebra i prosty rachunek. Wymaga również algebry macierzy, liczb zespolonych, teorii prawdopodobieństwa i równań różniczkowych cząstkowych.
- Fizycy nie są pewni, co niektóre z równań QM mówią nam o rzeczywistym świecie.
- QM sugeruje, że atomy i cząstki subatomowe zachowują się w dziwny sposób, zupełnie niepodobny do niczego, co widzimy w naszym codziennym życiu.
- QM opisuje rzeczy, które są niezwykle małe, więc nie możemy zobaczyć niektórych z nich bez specjalnego sprzętu, a wielu z nich nie możemy zobaczyć w ogóle.
QM opisuje naturę w sposób, który różni się od tego, w jaki zazwyczaj myślimy o nauce. Mówi nam, jak prawdopodobne jest zajście pewnych rzeczy, a nie mówi, że na pewno się wydarzą.
Jednym z przykładów jest eksperyment Younga z podwójną szczeliną. Jeśli wystrzelimy pojedyncze fotony (pojedyncze jednostki światła) z lasera na arkusz kliszy fotograficznej, zobaczymy pojedynczą plamkę światła na wywołanej kliszy. Jeśli umieścimy pomiędzy nimi arkusz metalu i zrobimy dwie bardzo wąskie szczeliny w arkuszu, to gdy wystrzelimy wiele fotonów na arkusz metalu, a one będą musiały przejść przez szczeliny, zobaczymy coś niezwykłego. Na całej powierzchni wywołanego filmu zobaczymy serię jasnych i ciemnych pasm. Możemy użyć matematyki, aby dokładnie określić, gdzie będą te jasne pasma i jak jasne było światło, które je utworzyło, to znaczy, możemy z wyprzedzeniem powiedzieć, ile fotonów padnie na każde pasmo. Ale jeśli spowolnimy proces i zobaczymy, gdzie każdy foton wyląduje na ekranie, nigdy nie będziemy w stanie powiedzieć z wyprzedzeniem, gdzie pojawi się następny. Możemy wiedzieć na pewno, że jest najbardziej prawdopodobne, że foton trafi w centralne jasne pasmo, i że staje się coraz mniej prawdopodobne, że foton pojawi się w pasmach coraz dalej od centrum. Wiemy więc na pewno, że pasma będą najjaśniejsze w centrum i coraz ciemniejsze dalej. Ale nigdy nie wiemy na pewno, który foton trafi do którego pasma.
Jednym z dziwnych wniosków płynących z teorii QM jest efekt "kota Schrödingera". O pewnych własnościach cząstki, takich jak jej położenie, prędkość ruchu, kierunek ruchu i "spin", nie można mówić, dopóki coś ich nie zmierzy (na przykład foton odbijający się od elektronu byłby pomiarem jego położenia). Przed pomiarem cząstka znajduje się w "superpozycji stanów", w której jej właściwości mają wiele wartości w tym samym czasie. Schrödinger powiedział, że mechanika kwantowa zdaje się mówić, że jeśli coś (np. życie lub śmierć kota) jest zdeterminowane przez zdarzenie kwantowe, to jego stan będzie zdeterminowany przez stan, który wynika ze zdarzenia kwantowego, ale tylko w czasie, gdy ktoś patrzył na stan zdarzenia kwantowego. W czasie przed spojrzeniem na stan zdarzenia kwantowego, być może "żywy i martwy kot (wybaczcie wyrażenie) [są] wymieszane lub rozmazane w równych częściach."
Zredukowana stała Plancka
Ludzie często używają symbolu ℏ {displaystyle \hbar } 

Przykład
Cząstka w jednowymiarowej studni jest najprostszym przykładem pokazującym, że energia cząstki może mieć tylko określone wartości. Mówi się, że energia jest "skwantowana". Studnia ma zerową energię potencjalną wewnątrz pewnego zakresu i ma nieskończoną energię potencjalną wszędzie poza tym zakresem. Dla przypadku jednowymiarowego w 
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . {{displaystyle -{frac {{hbar ^{2}}{2m}}}{{frac {d^{2}}}}=E ψ . }
Korzystając z równań różniczkowych, widzimy, że ψ {{displaystyle \psi } 
ψ = A e i k x + B e - i k x E = ℏ 2 k 2 2 m {{displaystyle \\psi =Ae^{ikx}+Be^{-ikx} \;\;\;E={frac {\hbar ^{2}k^{2}}{2m}}}.
lub
ψ = C sin k x + D cos k x {displaystyle ψ =C sin kx+D cos kx; } 
Ściany pudełka oznaczają, że funkcja falowa musi mieć szczególną postać. Funkcja falowa cząstki musi być zerowa w każdym przypadku, gdy ściany są nieskończenie wysokie. Przy każdej ścianie:
ψ = 0 a t x = 0 , x = L {displaystyle ®psi =0, ®mathrm {at} ® x=0,® x=L}
Rozważmy x = 0
- sin 0 = 0, cos 0 = 1. Aby spełnić
warunek ψ = 0, należy usunąć człon cos. Stąd D = 0
Teraz rozważmy: ψ = C sin k x { {scriptstyle ψ =C sin kx; }
- przy x = L, ψ = C sin k L = 0 { {displaystyle \scriptstyle \psi =C sin kL=0; }
- Jeśli C = 0 to ψ = 0 {dla wszystkich x.
To rozwiązanie nie jest użyteczne.
- zatem sin kL = 0 musi być prawdziwe, co daje nam
k L = n π n = 1 , 2 , 3 , 4 , 5 , . . . { {displaystyle kL=n \i \i \i n=1,2,3,4,5,...\i; }
Widzimy, że n {styl n} 
Powiązane strony
- Fala elektromagnetyczna
- Elektron
- Foton
- Splątanie kwantowe
- Równanie Schrödingera
Pytania i odpowiedzi
P: Co to jest mechanika kwantowa?
O: Mechanika kwantowa jest dziedziną fizyki, która wyjaśnia, jak działa wszechświat w skali mniejszej niż atomy. Znana jest również jako fizyka kwantowa lub teoria kwantowa.
P: Co oznacza termin "kwantowy"?
O: Termin "kwant" pochodzi z łaciny i oznacza "ile". Kwant energii to najmniejsza możliwa ilość (lub najmniejsza dodatkowa ilość), a mechanika kwantowa opisuje, jak ta energia porusza się lub oddziałuje.
P: Co to są cząstki subatomowe?
O: Cząstki subatomowe to cząstki tworzące atomy, takie jak protony, neutrony i elektrony. Są one nawet mniejsze od atomów.
P: W jaki sposób mechanika kwantowa opisuje działanie tych cząstek?
O: Mechanika kwantowa dostarcza reguł matematycznych do badania cząstek subatomowych i fal elektromagnetycznych, aby zrozumieć ich zachowanie i wzajemne oddziaływanie.
P: Co to jest dualizm fala-cząstka?
O: Dualizm falowo-cząsteczkowy odnosi się do faktu, że zarówno cząstki, jak i fale mogą zachowywać się podobnie - nie są to dwa odrębne byty, lecz raczej coś w rodzaju obu połączonych w jedno zjawisko.
P: Jak można opisać współczesną fizykę za pomocą mechaniki kwantowej?
O: Współczesną fizykę i chemię można wyjaśnić, stosując do nich matematyczne zasady mechaniki kwantowej.
Przeszukaj encyklopedię







