Zasada nieoznaczoności

Schematy

1. 1. Fotony, elektrony i inne cząstki subatomowe osiągną ostrość przy fotografowaniu przez dużą dziurę, ale nie wiemy dokładnie, gdzie znajdowały się w połowie drogi.


2. Zwężając otwór zaginamy ścieżki cząsteczek wokół krawędzi otworu (dyfrakcja), dzięki czemu powstała wiązka staje się większa i bardziej miękka.


3. Zwężając otwór zwiększamy pewność, gdzie foton znajduje się w środku, ale wtedy jego kierunek od tego miejsca do ekranu detekcji po prawej stronie staje się odpowiednio bardziej niepewny. Ognisko staje się niewyraźne. Poszerzenie otworu powoduje, że wszystkie fotony kończą się w środku ekranu detekcji, ale wtedy mamy mniejsze pojęcie o tym, gdzie były, gdy przechodziły przez centralną barierę.


4. Sprężyna mocująca barierę z małym otworem powoduje, że cząstka przeciska się przez otwór, który popycha barierę, naciąga sprężyny, a więc mierzy moment obrotowy. Ponieważ jednak bariera zamontowana na sprężynie porusza się, mamy mniejszą pewność, gdzie znajdowała się cząstka, gdy przechodziła przez otwór, a dyfrakcja wpłynie również na jej położenie na ekranie detektora.


5. Zawieszenie środkowej szczeliny za pomocą skal sprężynowych pozwala na pomiar pędu, ale czyniąc to w sposób nieprzewidywalny przesuwa szczelinę, co powoduje utratę informacji o położeniu każdego fotonu w środku.


6. Animacja ta pokazuje jedną z ważnych konsekwencji niepewnej natury wszechświata: kwantowe tunelowanie elektronów. Przyjrzyj się uważnie. Za każdym razem, gdy trochę przebije się przez barierę.

Jak ludzie dowiedzieli się o niepewności?

Bardzo krótko po tym, jak Werner Heisenberg stworzył nową fizykę kwantową, z jego matematyki wyszło coś nieoczekiwanego, wyrażenie:

Δ x Δ p ≳ h 4 π \\Delta x\, \Delta p\gtrsim \frac {h}{pi \i0} \i1}qquad \i1quad \i0}

Zakres błędu w pozycji (x) razy zakres błędu w pędzie (p) jest mniej więcej równy lub większy od stałej Plancka podzielonej przez 4π.

Te symbole wpisane w matematykę tworzą to, co już widzieliście na zdjęciach powyżej. Symbole te mówią wyraźnie, że nie można być całkowicie pewnym, gdzie coś jest i dokąd zmierza. Jeśli w każdej chwili masz większą jasność co do tego, gdzie to jest, to masz mniejsze pojęcie o tym, dokąd to zmierza i jak szybko. Jeżeli w dowolnym momencie będziesz miał większą jasność co do tego, dokąd zmierza i jak szybko, to mniej będziesz miał pojęcia o tym, gdzie teraz się znajduje.

Naukowcy już wcześniej dowiedzieli się, dlaczego niektóre substancje wydzielają charakterystyczne kolory światła, gdy są ogrzewane lub w inny sposób podniecone. Heisenberg próbował wyjaśnić, dlaczego każda z tych substancji ma charakterystyczną jasność. Nie byłoby wystarczająco dobrze, gdyby on i inni naukowcy powiedzieli: "Cóż, tak właśnie jest." Byli pewni, że musi istnieć dobry powód dla tych różnic, a także dla faktu, że proporcje pomiędzy mocami jasnych linii były zawsze takie same dla każdej próbki elementu.

Nie miał pojęcia, że potknie się o ukrytą tajemnicę natury, gdy wyruszył, by odkryć wyjaśnienie dla intensywności kolorowych linii charakterystycznych dla każdego z elementów. Badania mechaniki kwantowej wykazały już, dlaczego wodór ma cztery jasne linie w tej części widma, którą widzi człowiek. Musiało się wydawać, że następną rzeczą, której należało się nauczyć, będzie po prostu jak obliczyć ich jasność. Wodór wydawał się być oczywistym punktem wyjścia, ponieważ wodór ma do czynienia tylko z jednym elektronem i tylko z czterema liniami w widzialnej części widma. Z pewnością musi istnieć dobry powód, dla którego nie są one tak samo jasne. Wyjaśnienie jasności różnokolorowych linii neonu i innych pierwiastków może poczekać.

 

Heisenberg rozpoczął pracę nad fizyką kwantową, dostosowując klasyczne równania dla elektryczności, które są bardzo skomplikowane na początku, więc matematyka stojąca za jego pracą z 1925 roku była bardzo trudna do naśladowania.

Starał się znaleźć właściwy sposób na obliczenie intensywności jasnych linii w spektrum lamp wodorowych. Musiał znaleźć odpowiednią wielkość zwaną "amplitudą" i pomnożyć amplitudę przez amplitudę (lub inaczej mówiąc, musiał ją kwadratować), aby uzyskać pożądane natężenie. Musiał znaleźć sposób na wyrażenie amplitudy w sposób uwzględniający fakt, że lampy wodorowe nie promieniują na wszystkich częstotliwościach i nie promieniują w ciągłym zakresie częstotliwości w tej części widma, którą ludzie mogą zobaczyć. Heisenberg znalazł niezwykły nowy sposób obliczania amplitudy.

Dziwne równanie|równanie, które Heisenberg odkrył i używał do zwielokrotnienia jednej wielkości kwantowej (np. pozycji) przez inną (np. rozmachu), zostało opublikowane w tak zwanej "magicznej" pracy Heisenberga z lipca 1925 roku".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\i1}styk C(n,n-b)=\i0}suma _{a}^{\i1}, A(n,n-a)B(n-a,n-b)}

Powyższa matematyka wygląda bardzo ciężko, ale matematyka prowadząca do niej jest bardzo trudna i niezwykle trudna do zrozumienia. Podaje się ją tutaj tylko po to, aby pokazać, jak wyglądała. Papier Heisenberga to historyczny punkt orientacyjny. Wielu fizyków, którzy czytali jego pracę, mówiło, że nie mogą nie zgadzać się z jego wnioskami, ale nie mogą śledzić jego wyjaśnienia, jak doszedł do tych wniosków. Początkowe równania, których użył Heisenberg, dotyczyły serii Fouriera i obejmowały wiele czynników. Wrócimy do powyższego równania, ponieważ jest to swego rodzaju przepis na wypisywanie i mnożenie matryc.

Nowe równania musiały być tak dziwne i niezwykłe, ponieważ Heisenberg opisywał dziwny świat, w którym niektóre rzeczy, takie jak orbity elektronów, powoli nie powiększają się lub zmniejszają. Nowe rodzaje zmian wiążą się ze skokami i dużymi odstępami pomiędzy skokami. Elektrony mogą skakać tylko pomiędzy pewnymi orbitami, a energia uzyskana lub utracona w wyniku zmiany pomiędzy orbitami jest wytwarzana, gdy foton odpowiedniej energii zostanie wchłonięty lub zostanie wyprodukowany nowy foton odpowiedniej energii. Jeżeli elektrony w atomach wodoru najczęściej skaczą w dół (opadają) pomiędzy dwiema poszczególnymi orbitami, wtedy więcej fotonów zostanie wyemitowanych na tym poziomie energii, a więc światło wyprodukowane na tym poziomie będzie najbardziej intensywne.

Trudno było wykonać równania zbudowane dla widm ciągłych (co widzisz, gdy przepuszczasz światło słoneczne przez pryzmat) pasujące do widm, które mają tylko kilka szczytowych częstotliwości, między którymi nie ma nic. Prawie wszystko, co zostało już poznane na temat światła i energii, zostało zrobione z dużymi przedmiotami, takimi jak palące się świece czy słońce, a te duże przedmioty wytwarzają ciągłe widma. Nawet jeśli te zwyczajne rzeczy były łatwe do zrobienia w eksperymentach, to i tak zajęło dużo czasu, aby ustalić prawa (fizyki), które nimi rządzą. Teraz fizycy zajmowali się rzeczami zbyt małymi, by je zobaczyć, rzeczami, które nie wytwarzają ciągłych widm, i starali się znaleźć sposób, by przynajmniej uzyskać wskazówki, z tego co już wiedzieli, które pomogą im znaleźć prawa tych małych i wydobytych źródeł światła.

Oryginalne równania dotyczyły rodzaju wibrującego ciała, które wytwarzałoby falę, trochę tak jak trzcina w organie wytwarzałaby falę dźwiękową o charakterystycznej częstotliwości. Był więc ruch do tyłu i do przodu (jak wibrowanie trzciny) i była fala emitowana, którą można było uchwycić jako sinusoidę. Duża część tego, co wcześniej odkryto na temat fizyki na poziomie atomowym, miała związek z elektronami poruszającymi się wokół jąder. Kiedy masa porusza się na orbicie, kiedy obraca się wokół jakiejś piasty, ma to, co nazywa się "pędem kątowym". Pęd kątowy to sposób, w jaki coś w rodzaju karuzeli będzie się dalej obracać po tym, jak ludzie przestaną ją pchać. Matematyka używana do obliczeń fazowych i momentu pędu jest skomplikowana. Ponadto Heisenberg nie pokazał wszystkich swoich obliczeń w swojej pracy z 1925 roku, więc nawet dobrzy matematycy mogą mieć problem z wypełnieniem tego, czego nie powiedział.

Mimo że wielu fizyków twierdziło, że nie są w stanie zrozumieć różnych etapów matematycznych w przełomowym artykule Heisenberga, jeden z ostatnich artykułów, który próbuje wyjaśnić, jak Heisenberg uzyskał swój wynik, wykorzystuje dwadzieścia wypełnionych matematycznie stron. Nawet ten artykuł nie jest łatwy do zrozumienia. Matematyka zaczęła się od kilku naprawdę twardych rzeczy i w końcu przyniosła coś stosunkowo prostego, co jest pokazane na górze tego artykułu. Uzyskanie prostszego wyniku nie było łatwe i nie będziemy starali się pokazać procesu przechodzenia od przestarzałego obrazu wszechświata do nowej fizyki kwantowej. Potrzebujemy tylko wystarczającej ilości szczegółów, aby pokazać, że prawie natychmiast po tym, jak Heisenberg dokonał przełomu, część tego, jak działa wszechświat, której nikt wcześniej nie widział.

Heisenberg musiał być bardzo podekscytowany, ale też bardzo zmęczony, kiedy późną nocą dokonał wreszcie przełomu i zaczął sobie udowadniać, że to się uda. Niemal od razu zauważył coś dziwnego, coś, co uważał za irytujący mały problem, który mógł jakoś rozwiązać. Ale okazało się, że ta mała uciążliwość była wielkim odkryciem.

Heisenberg pracował nad pomnożeniem amplitud przez amplitudy, a teraz Heisenberg miał dobry sposób na wyrażenie amplitudy za pomocą swojego nowego równania. Naturalnie myślał o mnożeniu i o tym, jak będzie mnożyć rzeczy, które zostały podane w postaci skomplikowanych równań.

Heisenberg zdał sobie sprawę, że poza zwiększeniem amplitudy, chciałby w końcu pomnożyć pozycję przez pęd, czy też pomnożyć energię przez czas, i wyglądało na to, że w tych nowych przypadkach zmieniłby porządek. Heisenberg uważał, że nie powinno mieć znaczenia, czy pomnożymy pozycję przez pęd, czy też pomnożymy pęd przez pozycję. Gdyby były to tylko proste liczby, nie byłoby problemu. Ale oba były skomplikowanymi równaniami, a to, jak dostałeś liczby, które należało podłączyć do równań, okazało się różne w zależności od tego, w jaki sposób zacząłeś. W naturze musiałeś zmierzyć pozycję, a następnie pęd, albo musiałeś zmierzyć pęd, a następnie pozycję, i w matematyce przeważyła ta sama ogólna sytuacja. (Zobacz artykuł w angielskiej Wikipedii, Heisenberg, wejście do mechaniki macierzowej, jeśli chcesz poznać skomplikowane szczegóły!) Niewielkie, ale brzydkie różnice pomiędzy wynikami miały pozostać, nieważne jak bardzo Heisenberg chciałby, aby zniknęły.

W tym czasie Heisenberg nie mógł pozbyć się tego małego problemu, ale był wyczerpany, więc przekazał swoją pracę swojemu bezpośredniemu przełożonemu, Maxowi Bornowi, i pojechał na wakacje.

Max Born był niezwykłym matematykiem, który wkrótce przekonał się, że równanie, które dał mu Heisenberg, było swego rodzaju przepisem na napisanie matrycy. Dr Born był jedną z niewielu osób, które w tamtym czasie interesowały się tym dziwnym rodzajem matematyki, o którym większość ludzi uważała, że nie jest zbyt dobry. Wiedział, że matryce można mnożyć, więc wszystkie obliczenia dotyczące rozliczania jednego problemu fizyki można było wykonać poprzez pomnożenie jednej matrycy przez drugą. Samo umieszczenie skomplikowanej procedury w standardowej i akceptowalnej formie ułatwiłoby pracę z nią. Mogłoby to również ułatwić innym ludziom akceptację.

Urodzony był tak dobrym matematykiem, że niemal natychmiast zdał sobie sprawę, iż zmiana kolejności mnożenia obu matryc da inny wynik, a wyniki będą się różnić o niewielką ilość. Ilość ta wynosiłaby h/2πi. W codziennym życiu ta różnica byłaby tak mała, że nie moglibyśmy jej nawet zobaczyć.

Kiedy pewne molekuły są podniecone, wydają charakterystyczny kolor.


Widmo wodorowe


Widmo neonowe


Pełne spektrum wizualne słońca. Nie ma żadnych przerw. Ten wykres pokazuje natężenia na różnych częstotliwościach.


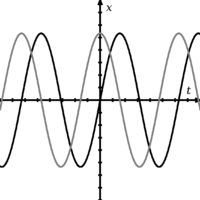
Dwie fale, które są ze sobą niefazowe

Na temat formalnej teorii niepewności

Zajęło to kilka lat, ale Heisenberg był w stanie udowodnić Zasadę Niepewności, która mówi, że Δx × Δp = h/2, czyli liczba, która wychodzi z pierwotnych równań, ale pomija π i i, które mają związek ze zmianami fazowymi. Heisenberg wyjaśnił, że swoją zasadę niepewności wyprowadził z tego wcześniejszego wyniku, gdy w 1927 r. napisał pracę wprowadzającą tę teorię.

Stała pisana h, zwana stałą Plancka, jest tajemniczą liczbą, która często się pojawia, więc musimy zrozumieć, czym jest ta maleńka liczba. Numerycznie, zazwyczaj jest ona podawana jako 6,62607×10^-34 J s (dżul sekund). Jest to więc liczba, która wiąże się z energią i czasem.

Został on odkryty, kiedy Planck uświadomił sobie, że energia idealnego grzejnika (zwanego grzejnikiem ciała czarnego) jest emitowana w jednostkach o określonej wielkości zwanych "kwantami" (osobnik tego słowa to "kwant"). Wypromieniowana energia jest emitowana w postaci fotonów, a częstotliwość fotonu jest proporcjonalna do "uderzenia", które dostarcza. Doświadczamy różnych częstotliwości światła widzialnego jako różnych kolorów. Na fioletowym końcu spektrum każdy foton ma stosunkowo dużą ilość energii; na czerwonym końcu spektrum każdy foton ma stosunkowo małą ilość energii. Sposób obliczenia ilości energii fotonu jest podany za pomocą równania E = hν (energia równa się stałej Plancka razy "nu" lub częstotliwości).

Zasada niepewności Heisenberga Δx × Δp ≥ h mówi nam, że za każdym razem, gdy próbujemy przypiąć pewne pary liczb, możemy się tylko tak zbliżyć, i że jeżeli spróbujemy na jednej z nich uzyskać większą jasność, tzn. jeżeli spróbujemy zmniejszyć Δx, aby mieć lepsze wyobrażenie o pozycji czegoś, to będziemy musieli otrzymać z powrotem większą liczbę dla drugiej pary, i że kwota, o którą te dwie są oddalone, jest ściśle związana z h.

Kolejna para wielkości fizycznych idzie zgodnie z zależnością niepewności: ΔE × Δt ≥ h, a para ta wskazuje, między innymi, że jeśli spojrzymy w przestrzeni międzygwiezdnej, w jakimś miejscu, w którym nie spodziewalibyśmy się niczego znaleźć, i zmniejszymy Δt coraz bliżej i bliżej do zera, to aby utrzymać równowagę pokazaną w równaniu ΔE musi być coraz większa - i nagle coś z pędem może powstać tylko na ten krótki okres czasu.

Jak można wyjaśnić tę nieokreśloność (brak pewności)? Co się dzieje we Wszechświecie? Często mówi się, że nowa, udana teoria może dostarczyć nowych informacji o badanych zjawiskach. Heisenberg stworzył model matematyczny, który przewidywał prawidłowe natężenia dla jasnej linii widma wodoru, ale nie zamierzając tego zrobić odkrył, że pewne pary wielkości fizycznych ujawniają nieoczekiwaną niepewność. Do tej pory nikt nie miał pojęcia, że pomiary nie mogą być wiecznie dokonywane coraz dokładniej i dokładniej. Fakt, że nie można było ich uczynić pewniejszymi, bardziej definitywnymi, był oszałamiającym nowym odkryciem. Wiele osób nie chciało się z tym pogodzić.

Bohr i jego koledzy argumentowali, że fotony, elektrony itp. nie mają ani pozycji, ani pędu, dopóki nie zostaną zmierzone. Ta teoretyczna pozycja wyrosła z odkrycia niepewności, a nie była tylko jakąś osobistą preferencją co do tego, w co wierzyć. Bohr powiedział, że nie wiemy nic o czymś takim jak foton czy elektron, dopóki go nie zobaczymy. Aby obserwować tak małą rzecz musimy jakoś z nią współdziałać. W codziennym życiu można zrobić coś takiego, jak chodzić obok samochodu, zaznaczając jednocześnie czasy, w których się on przecina, na siatce narysowanej na chodniku. Być może waga samego samochodu przyciśnie małe dźwignie w chodniku, które wyłączają zegary przymocowane do każdego z nich i zapisują wagę samochodu. W końcu będziemy mieli jasny zapis, gdzie samochód znajdował się w różnych momentach, a także będziemy mogli obliczyć jego kierunek postępu i wagę. Moglibyśmy wtedy w dowolnym momencie na zegarze poznać zarówno jego pozycję, jak i pęd (jego prędkość pomnożoną przez masę). Nie wyobrażalibyśmy sobie nawet, że siła potrzebna do poruszania tymi małymi dźwigniami będzie miała jakikolwiek wpływ na postęp samochodu. Nie wyobrażalibyśmy sobie również, że samochód nie ma położenia ani trajektorii pomiędzy punktami na chodniku, gdzie znajdują się dźwignie, albo że samochód istnieje w tym czasie w swego rodzaju trójwymiarowym rozmyciu i osiada tylko podczas naciskania dźwigni. Świat, który znamy, nie ujawnia tych dziwnych rodzajów interakcji.

Aby zlokalizować statek na morzu w najciemniejszą noc, moglibyśmy użyć reflektora i światło to nie zakłóciłoby pozycji lub kierunku podróży statku, ale zlokalizowanie elektronu ze światłem wymagałoby uderzenia go jednym lub kilkoma fotonami, z których każdy miałby wystarczający pęd do zakłócenia pozycji i trajektorii elektronu. Zlokalizowanie elektronu za pomocą innych środków wiązałoby się z utrzymaniem go w pewnego rodzaju fizycznym unieruchomieniu, które również zakończyłoby jego ruch do przodu.

Aby zlokalizować foton, najlepsze, co można zrobić bez przerywania jego ruchu do przodu, to sprawić, że przejdzie on przez okrągły otwór w barierze. Jeśli znamy czas, w którym foton został wyemitowany (np. przez laser) i czas, w którym foton dotarł na ekran wykrywający, taki jak aparat cyfrowy, wówczas możemy obliczyć czas potrzebny do przebycia tej odległości i czas, w którym foton przechodził przez otwór. Jednakże, aby foton mógł przez niego przejść, okrągły otwór musi mieć średnicę większą niż rozmiar fotonu. Im mniejszy okrągły otwór, tym bliżej znamy dokładne położenie fotonu w czasie jego przechodzenia. Nigdy jednak nie możemy się dowiedzieć, czy foton znajduje się w tym czasie poza centrum. Jeśli otwór jest dokładnie tej samej wielkości co foton, to nie przejdzie przez niego. W miarę zmniejszania się średnicy otworu coraz bardziej zmienia się pęd lub kierunek fotonu opuszczającego otwór.

Niels Bohr i jego koledzy argumentowali, że wpadamy w duże tarapaty, jeśli założymy, że to, co jest zbyt małe, by można było to zobaczyć nawet pod mikroskopem, to wszystko, na co mamy dowód tylko na skalę życia codziennego. W życiu codziennym sprawy mają zawsze określoną pozycję. W skali atomowej nie mamy żadnych dowodów na poparcie tego wniosku. W codziennym życiu, rzeczy mają określony czas, w którym się pojawiają. W skali atomowej, nie mamy żadnych dowodów na poparcie tego wniosku. W życiu codziennym, jeśli obserwuje się fabrykę od nocnej zmiany dnia pierwszego do dziennej zmiany dnia drugiego i widzi się gotowy samochód wrzucony do doku przeładunkowego, nie ma sensu mówić, że nie da się stwierdzić, czy został dostarczony na nocnej zmianie, czy na dziennej zmianie. Ale w skali atomowej możemy pokazać przypadki, w których musimy liczyć jeden foton jako wyprodukowany dwa razy. (Jeśli to nie wystarczy, możemy również pokazać przypadki, w których pojedynczy foton został wyprodukowany z dwóch sąsiednich laserów).

Częścią trudności z ustaleniem, co dzieje się w skali atomowej jest to, że chcielibyśmy wiedzieć zarówno gdzie coś jest i jaka jest jego trajektoria, jak i wiedzieć obie rzeczy jednocześnie, ale nie możemy mierzyć zarówno pozycji, jak i trajektorii w tym samym czasie. Albo mierzymy moment pędu fotonu lub elektronu w tym samym czasie, a następnie bez większego opóźnienia niż to konieczne mierzymy jego położenie, albo zmieniamy rzeczy i mierzymy najpierw położenie, a potem pęd. Problem polega na tym, że dokonując pierwszego pomiaru przybieramy dość konkretną postać (ściskając ją w jakiś sposób) zwiększamy niepewność związaną z kolejnym pomiarem. Gdyby nasze początkowe pomiary były tak surowe, że w każdym z nich wprowadzono wiele błędów, to moglibyśmy poprawić sytuację, używając lżejszego dotyku do każdego z nich, ale nigdy nie moglibyśmy przekroczyć pewnej granicy dokładności.

Z codziennego życia wiemy, że próba zważenia czegoś na wadze łazienkowej umieszczonej na pralce w cyklu wirowania przyniesie niedokładne wyniki, ponieważ igła na wadze będzie się źle trząść. Możemy wyłączyć pralkę. Jednak przy bardzo dokładnych pomiarach okazuje się, że przejeżdżające po okolicy ciężarówki powodują, że igła się porusza, więc możemy umieścić wagę na czymś, co będzie ją izolować od zewnętrznych zakłóceń. Wierzymy, że możemy wyeliminować wibracje na tyle, aby wyniki były tak dokładne, jak chcemy. Nigdy nie uważamy, że rzecz na skali sama w sobie wibruje lub że ma nieokreślony pęd.

Argumentując wstecz w stosunku do Zasady Niepewności, wygląda na to, że w rzeczywistości nie ma żadnej konkretnej pozycji i żadnego konkretnego pędu dla jakiejkolwiek rzeczy w skali atomowej i że eksperymentatorzy mogą tylko zmusić rzeczy do definitywności w granicach określonych przez Zasadę Niepewności. Bohr i jego koledzy argumentowali tylko, że nie możemy nic wiedzieć bez wykonania pomiarów, a kiedy pomiary zostały wykonane, możemy popchnąć rzeczy w kierunku bardziej określonej pozycji lub bardziej określonego pędu, ale nie możemy uzyskać absolutnej definitywności lub pewności, której byśmy chcieli. Ale inni potraktowali tę możliwość poważnie i argumentowali, że jeśli matematyka jest słuszna, to nie może być absolutnej definitywności czy pewności w świecie ultra małych. Natura nauki polega na tym, że matematyka jest tylko modelem rzeczywistości i nie ma żadnej gwarancji, że jest to właściwy model.

Matematyka i praktyczne konsekwencje tego, co przewiduje matematyka, są tak wiarygodne, że trudno się z nimi nie zgodzić, ale to, co mówi matematyka o rzeczywistym świecie, doprowadziło do powstania kilku różnych pomysłów. Wśród naukowców, którzy współpracowali z Nielsem Bohrem w Kopenhadze, zasada niepewności została przyjęta w taki sposób, że na poziomie elementarnym fizyczny wszechświat nie istnieje w formie deterministycznej. Jest to raczej zbiór prawdopodobieństw lub potencjałów.

W przeciwieństwie do historii utkanej wokół matematyki przez grupę kopenhaską, istnieją inne historie, takie jak "interpretacja wielu wszechświatów", która mówi, że za każdym razem, gdy istnieje wiele możliwych wyników zgodnie z teorią kwantową, każdy wynik występuje w swoim nowym wszechświecie. Einstein argumentował, że nie ma wielu możliwych wyników, więc istnieje tylko jeden wszechświat i jest on zdeterminowany, lub, jak to ujął, "Bóg nie gra w kości".

Gdyby h było najmniejszą możliwą ilością energii, to podstawowe równanie pokazujące energię zawartą w fotonach o różnej częstotliwości nie balansowałoby. Byłoby ono błędne.

Zastrzeżenia dotyczące zasady niepewności

Albert Einstein zauważył, że nowa mechanika kwantowa implikuje brak pozycji i rozmachu w czasie poprzedzającym wykonanie pomiarów, i mocno się sprzeciwił. Mocno wierzył, że rzeczy mają określone pozycje i określony pęd zanim zostaną zmierzone, i że fakt, że zmierzenie jednej z par rzeczy i zakłócenie możliwości dokładnego zmierzenia drugiej nie przemawia za tym, że wcześniej nie było żadnego z nich. On i jego dwaj koledzy napisali to, co stało się znane jako "papier EPR". W artykule tym stwierdzono, że muszą istnieć cechy, które decydują o pozycji i rozmachu, i że jeśli moglibyśmy je zobaczyć, lub jeśli moglibyśmy uzyskać informacje na ich temat, wtedy moglibyśmy matematycznie poznać i przewidzieć pozycję i rozmach. Przez długi czas ludzie uważali, że nie ma sposobu na udowodnienie lub obalenie tego, co było dla Einsteina artykułem wiary. Argument ten był bardzo produktywny, ponieważ doprowadził do wszystkich współczesnych zmian w splątaniu.

Matematycznie, Einstein okazał się być w błędzie. W 1964 roku John Stewart Bell opracował matematyczną metodę rozróżnienia pomiędzy zachowaniem się dwóch cząstek, które określają stany, które są tylko nieznane dwóm badającym je osobnikom, a dwiema cząstkami, które zaplątały się w stany, które są nieokreślone lub niepewne, dopóki nie zostaną zmierzone. Jego metoda pokazuje, że prawdopodobieństwa uzyskania pewnych wyników są różne przy tych dwóch różnych założeniach. Jego praca nazywa się twierdzeniem Dzwonu lub Nierówność Dzwonu (Bell's Inequality). Eksperymenty pokazały, że natura zachowuje się tak, jak opisuje ją Bell.

Kolejna droga do niepewności

Początkowe dyskusje na temat zasady niepewności Heisenberga zależały od modelu, który nie uważał, że cząstki materii takie jak elektrony, protony itp. mają długość fali. W 1926 roku Louis de Broglie pokazał, że wszystkie rzeczy, nie tylko fotony, mają swoją własną częstotliwość. Rzeczy mają charakter falowy i cząstkowy, podobnie jak fotony. Jeśli spróbujemy sprawić, by fala czegoś takiego jak proton była węższa i wyższa, uczyniłoby to jego pozycję bardziej przejrzystą, ale wtedy pęd byłby mniej dobrze zdefiniowany. Jeśli spróbujemy sprawić, by pęd w opisie fali był wyraźniejszy, tzn. by pozostawał w węższym zakresie wartości, to szczyt fali rozproszy się i jego pozycja stanie się mniej wyraźna.

Fala, która jest częścią opisu fotonu, w mechanice kwantowej nie jest tym samym rodzajem rzeczy, co fala na powierzchni oceanu lub regionów sprężonego powietrza i rzadkiego powietrza, które składają się na fale dźwiękowe. Zamiast tego fale te mają szczyty lub obszary o wysokiej amplitudzie, które mają związek z prawdopodobieństwem znalezienia czegoś w tym momencie w przestrzeni i czasie. Dokładniej mówiąc, to właśnie kwadrat amplitudy daje prawdopodobieństwo pojawienia się jakiegoś zjawiska.

Fala, która odnosi się do fotonu może być czystą sinusoidą. W takim przypadku kwadrat wartości każdego szczytu dawałby prawdopodobieństwo zaobserwowania fotonu w tym punkcie. Ponieważ amplitudy fal sinusoidalnych są wszędzie takie same, prawdopodobieństwo znalezienia fotonu w każdym z nich byłoby takie samo. Tak więc, praktycznie rzecz biorąc, znajomość fali dla jednego z tych fotonów nie dawałaby żadnej wskazówki, gdzie go szukać. Z drugiej strony, moment pędu fotonu jest matematycznie związany z amplitudą jego fali. Ponieważ w tym przypadku mamy czystą sinusoidę, amplituda każdego cyklu tej fali jest taka sama i dlatego z falą tą związana jest tylko jedna wartość momentu pędu. Nie wiedzielibyśmy gdzie foton uderzyłby, ale wiedzielibyśmy dokładnie jak mocno uderzyłby.

W wiązkach światła, które skupiają się na pewnym punkcie na ekranie wykrywania, fale związane z fotonami nie są czystymi sinusoidami. Są to raczej fale o wysokiej amplitudzie w jednym punkcie i znacznie niższej amplitudzie po obu stronach tego najwyższego szczytu. Z matematycznego punktu widzenia możliwe jest przeanalizowanie takiej fali na kilka różnych sinusoidalnych fal o różnych długościach fali. Nieco łatwiej jest wizualizować odwrotną stronę tego procesu, patrząc na początkową sinusoidę o jednej częstotliwości, do której dodaje się drugą sinusoidę o innej długości fali, potem trzecią, potem czwartą, i tak dalej. Rezultatem będzie złożona fala pokazująca jeden wysoki szczyt i zawierająca dużą liczbę fal o różnych długościach fali, a więc o różnych pędach. W takim przypadku prawdopodobieństwo pojawienia się fotonu w pewnym momencie jest bardzo duże, ale pęd, który on dostarcza może okazać się związany z długością fali któregoś z komponentów. Innymi słowy, wartość p = ħ/λ nie jest już jedną wartością, ponieważ należy wziąć pod uwagę wszystkie długości zmontowanych "fal o różnej długości fali".

Symulacja pokazuje, jak matematycznie modelować wyostrzenie położenia cząstki: Nałożenie wielu różnych form fali na oryginalną sinusoidę. Centrum będzie tworzyło coraz wyższy szczyt, a reszta szczytów będzie zwiększona, ale zmniejszona, ponieważ będą się one wzajemnie zakłócać. Więc w końcu jest wiele różnych fal w superpozycji, każda o innej długości fali i (przez p = ħ/λ) inny pęd, ale tylko jeden bardzo wysoki szczyt, który rośnie coraz wyżej i węższy i daje nam coś bliżej i bliżej do określonej pozycji.

Aby rozmach był coraz bardziej zdecydowany, musielibyśmy zabierać coraz więcej nakładających się sinusoidalnych fal, aż do momentu, gdy pozostałaby nam tylko prosta sinusoidalna fala. W ten sposób stopniowo zmniejszalibyśmy wysokość centralnego szczytu i stopniowo zwiększalibyśmy wysokość konkurujących ze sobą miejsc, w których można by znaleźć cząstkę.

Kiedy więc zaczynamy od falowego obrazu subatomowych cząstek, to zazwyczaj mamy do czynienia ze stosunkowo wysokimi szczytami centralnymi i stosunkowo dużymi długościami fal składowych. W takich okolicznościach nigdy nie będzie można przewidzieć dokładnej pozycji lub dokładnego momentu pędu. Jeżeli model matematyczny jest dokładnym odwzorowaniem świata rzeczywistego, to żaden foton ani inna cząstka subatomowa nie ma ani dokładnego położenia, ani określonego pędu. Gdy mierzymy taką cząstkę, możemy wybrać metodę, która dodatkowo ściska pik i zawęża go, lub możemy wybrać metodę, która obniża pik i wyrównuje długości fal składowych. W zależności od tego, co mierzymy i jak to robimy, możemy sprawić, że nasza lokalizacja wyjdzie bardziej konkretna lub możemy zawęzić zakres pędów. Możemy zadbać o to, aby w eksperymencie nie było różnych sposobów szarpania aparatem, ale nie możemy pozbyć się tego, że nie było na początku nic całkowicie pewnego.

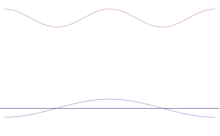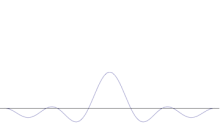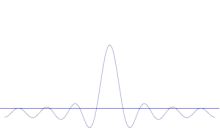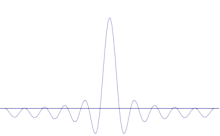
Superpozycja kilku fal płaskich. Pakiet fal staje się coraz bardziej zlokalizowany dzięki dodaniu wielu fal. Transformacja Fouriera jest operacją matematyczną, która dzieli pakiet fal na pojedyncze fale płaskie. Należy pamiętać, że pokazane tu fale są prawdziwe tylko dla celów ilustracyjnych, podczas gdy w mechanice kwantowej funkcja fal jest na ogół złożona.

Wpływy kulturowe

Najważniejszy wpływ Zasady Niepewności Heisenberga miał na argumenty dotyczące wolności woli. Zgodnie z teoriami fizyki klasycznej można argumentować, że prawa przyczyny i skutku są nieubłagane i że gdy tylko wszechświat rozpoczął się w pewien sposób, na podstawie tego stanu początkowego można obliczyć wzajemne oddziaływanie całej materii i energii, które ma nastąpić w przyszłości. Ponieważ wszystko jest absolutnie wynikiem tego, co było przed nim, argumentowali oni, że każda decyzja, którą podejmuje człowiek i każda sytuacja, w którą człowiek wchodzi, była z góry ustalona od początku czasu. Nie mamy więc żadnego wyboru w tym, co robimy.

Ludzie, którzy wierzą w wolność woli, argumentują, że prawa mechaniki kwantowej nie przewidują tego, co się wydarzy, a jedynie to, co jest bardziej i mniej prawdopodobne. Dlatego każde działanie jest wynikiem serii przypadkowych "rzutów monetą" i żadna decyzja nie może być przypisana do zbioru koniecznych warunków wstępnych.

Wyrażenia "skok kwantowy" i "skok kwantowy" stały się zwyczajnym sposobem mówienia o rzeczach. Zazwyczaj ludzie zamierzają opisać coś jako obejmujące ogromną zmianę, która następuje w krótkim okresie czasu. Termin ten odnosi się do sposobu, w jaki elektron zachowuje się w atomie albo kiedy pochłania foton przychodzący z zewnątrz i w ten sposób przeskakuje z jednej orbity wokół jądra atomu na wyższą, albo kiedy emituje foton i w ten sposób spada z wyższej orbity na niższą. Ideą Neilsa Bohra i jego współpracowników było to, że elektron nie przemieszcza się między orbitami, lecz znika z jednej orbity i natychmiast pojawia się na innej. Tak więc skok kwantowy to tak naprawdę nie jakaś ziemia burząca zmiany, ale nagła mała zmiana z jednej domeny na drugą.

Kiedy człowiek mierzy jakiś proces w skali subatomowej i objawia się zasada niepewności, to można powiedzieć, że działanie człowieka wpłynęło na to, co było mierzone. Dokonanie pomiaru mającego na celu jednoznaczne określenie położenia cząstki w sposób nieunikniony wpłynie na jej pęd i cokolwiek zostanie zrobione, aby zmierzyć ten pęd jak najszybciej po pomiarze jej położenia, nie można nie zmienić prawdopodobieństwa odkrycia momentu pędu. Tak więc zasada niepewności może wyjaśnić niektóre rodzaje interferencji wytwarzanych przez badaczy, które wpływają na wyniki eksperymentu lub obserwacji. Jednak nie wszystkie efekty obserwatorów wynikają z efektów kwantowych lub z zasady niepewności. Pozostałe to "efekty obserwatora", ale nie efekty niepewności kwantowej.

Efekty działania obserwatorów obejmują wszystkie rodzaje rzeczy, które działają w naszej zwykłej ludzkiej skali zdarzeń. Jeśli antropolog stara się uzyskać jasne wyobrażenie o życiu w prymitywnym społeczeństwie, ale jego obecność denerwuje społeczność, którą odwiedza, wówczas poczynione obserwacje mogą być bardzo mylące. Jednak żadna z istotnych interakcji nie zachodzi na poziomie opisanym przez mechanikę kwantową lub zasadę niepewności.

Czasami słowo "kwant" będzie używane do celów reklamowych, aby wskazać coś nowego i potężnego. Na przykład, producent małych silników benzynowych, Briggs i Stratton, ma jedną linię czterocylindrowych silników o niskiej mocy do kosiarek benzynowych i podobnych narzędzi ogrodowych, które nazywa "Quantum".

Więcej czytania

• Wprowadzenie teorii ilościowej, s. 115 i s. 158

J.P. McEvoy i Oscar Zarate