Całka powierzchniowa

Całki powierzchniowe pól skalarnych

Rozważmy powierzchnię S, na której zdefiniowane jest pole skalarne f. Jeśli pomyślimy o S jako o powierzchni wykonanej z pewnego materiału, a dla każdego x w S liczba f(x) jest gęstością materiału w x, to całka powierzchniowa f na S jest masą na jednostkę grubości S. (Jest to prawdziwe tylko wtedy, gdy powierzchnia jest nieskończenie cienką powłoką).) Jednym z podejść do obliczania całki powierzchniowej jest podzielenie powierzchni na wiele bardzo małych kawałków, przyjęcie, że na każdym kawałku gęstość jest w przybliżeniu stała, znalezienie masy na jednostkę grubości każdego kawałka przez pomnożenie gęstości kawałka przez jego powierzchnię, a następnie zsumowanie otrzymanych liczb, aby znaleźć całkowitą masę na jednostkę grubości S.

Aby znaleźć jednoznaczny wzór na całkę powierzchniową, matematycy parametryzują S poprzez rozważenie na S układu współrzędnych krzywoliniowych, takich jak szerokość i długość geograficzna na kuli. Niech taką parametryzacją będzie x(s, t), gdzie (s, t) zmienia się w pewnym obszarze T na płaszczyźnie. Wówczas całka powierzchniowa jest dana przez

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {displaystyle \\int _{S}f, dS= \iint _{T}f(\mathbf {x} (s,t))\left|{partial \mathbf {x} nad s} \times \partial {{partial \mathbf {x} \\ nad \partial t} \right|ds,dt}

gdzie wyrażenie między kreskami po prawej stronie jest wielkością iloczynu krzyżowego pochodnych cząstkowych x(s, t).

Na przykład, aby znaleźć pole powierzchni pewnego ogólnego kształtu funkcjonalnego, powiedzmy z = f ( x , y ) {displaystyle z=f,(x,y)}. , mamy

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {displaystyle A= ∫int _{S}},dS= ∫int _{T}  T  r ∂ x × ∂ r ∂ y ‖ d x d y \\ nad \partial x \ czas {\partial \mathbf {r} \over \partial y} \right|dx,dy}

gdzie r = ( x , y , z ) = ( x , y , f ( x , y ) ) { {r} =(x,y,z)=(x,y,f(x,y))} . Tak więc ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {{displaystyle {{partial \mathbf {{r}} ∂ r ∂ x}=(1,0,f_{x}(x,y))} , oraz ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) {{displaystyle {{partial \mathbf {{r}} ∂ r ∂ y}=(0,1,f_{y}(x,y))} . Zatem,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {displaystyle {{begin{aligned}}A&{}=iint _{T}left(1,0,{partial f nad \partial x}prawo)\times \left(0,1,{\partial f nad \partial y}prawo)\prawo|dx,dy\}{}=iint _{T} left(-{partial f \partial x},-{partial f \partial y},1}prawo)\prawo|dx,dy\&{}=iint _{T}{sqrt {left({partial f \partial x \\\right)^{2}+left({partial f \partial y \right)^{2}+1}}}}:\,dx,dy{aligned}}}

który jest wzorem na pole powierzchni ogólnego kształtu funkcjonalnego. Wektor w drugim wierszu powyżej można rozpoznać jako wektor normalny do powierzchni.

Zauważmy, że ze względu na obecność iloczynu krzyżowego, powyższe wzory działają tylko dla powierzchni osadzonych w przestrzeni trójwymiarowej.

Całki powierzchniowe pól wektorowych

Rozważmy pole wektorowe v na S, to znaczy, że dla każdego x w S, v(x) jest wektorem.

Całka powierzchniowa może być zdefiniowana składnikowo zgodnie z definicją całki powierzchniowej pola skalarnego; wynikiem jest wektor. Na przykład, dotyczy to pola elektrycznego w pewnym ustalonym punkcie ze względu na elektrycznie naładowaną powierzchnię, lub grawitacji w pewnym ustalonym punkcie ze względu na arkusz materiału. Można również obliczyć strumień magnetyczny przez powierzchnię.

Alternatywnie, matematycy mogą całkować składową normalną pola wektorowego; wynik jest skalarem. Przykładem może być płyn przepływający przez S, gdzie v(x) określa prędkość płynu w punkcie x. Strumień definiuje się jako ilość płynu przepływającego przez S w jednostce czasu.

Z ilustracji tej wynika, że jeśli pole wektorowe jest styczne do S w każdym punkcie, to strumień wynosi zero, ponieważ płyn płynie równolegle do S, ani do wewnątrz, ani na zewnątrz. Wynika z tego również, że jeśli v nie płynie tylko wzdłuż S, to znaczy, jeśli v ma zarówno składową styczną jak i normalną, to tylko składowa normalna przyczynia się do strumienia. Bazując na tym rozumowaniu, aby znaleźć strumień, musimy wziąć iloczyn punktowy v z jednostkową normalną powierzchniową do S w każdym punkcie, co da nam pole skalarne, i zintegrować otrzymane pole jak wyżej. Daje to wzór

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . { {displaystyle \int _{S}{\mathbf {v} } } \dot \,d{\mathbf {S} }=int _{S}({{mathbf {v} }}(\mathbf {n}})\, dS=int _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({{partial \mathbf {x} nad \partial s \times {\partial \mathbf {x} \\ nad \partial t}prawo)ds\,dt. }

Iloczyn krzyżowy po prawej stronie tego wyrażenia jest normalną powierzchniową określoną przez parametryzację.

Wzór ten definiuje całkę po lewej stronie (zwróć uwagę na kropkę i notację wektorową dla elementu powierzchniowego).

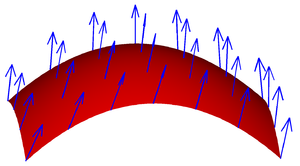
Pole wektorowe na powierzchni.

Twierdzenia dotyczące całek powierzchniowych

Różne użyteczne wyniki dla całek powierzchniowych mogą być wyprowadzone przy użyciu geometrii różniczkowej i rachunku wektorowego, takie jak twierdzenie o dywergencji i jego uogólnienie, twierdzenie Stokesa.

Zagadnienia zaawansowane

Zmiana parametryzacji

W powyższej dyskusji zdefiniowano całkę powierzchniową poprzez użycie parametryzacji powierzchni S. Dana powierzchnia może mieć kilka parametryzacji. Na przykład, gdy na sferze przesuniemy położenie bieguna północnego i południowego, to szerokość i długość geograficzna zmieni się dla wszystkich punktów na sferze. Naturalnym pytaniem jest więc, czy definicja całki powierzchniowej zależy od wybranej parametryzacji. Dla całek z pól skalarnych odpowiedź na to pytanie jest prosta, wartość całki powierzchniowej będzie taka sama bez względu na to, jakiej parametryzacji użyjemy.

Całki z pól wektorowych są bardziej skomplikowane, ponieważ w grę wchodzi normalna powierzchniowa. Matematycy udowodnili, że jeżeli mamy dwie parametryzacje tej samej powierzchni, których normalne powierzchniowe wskazują w tym samym kierunku, to obie parametryzacje dają tę samą wartość całki powierzchniowej. Jeżeli natomiast normale tych parametryzacji wskazują w przeciwnych kierunkach, to wartość całki powierzchniowej otrzymanej za pomocą jednej parametryzacji jest ujemna w stosunku do wartości otrzymanej za pomocą drugiej parametryzacji. Wynika z tego, że biorąc pod uwagę powierzchnię, nie musimy trzymać się żadnej unikalnej parametryzacji, ale podczas całkowania pól wektorowych musimy z góry zdecydować, w którą stronę będzie skierowana normalna, a następnie wybrać dowolną parametryzację zgodną z tym kierunkiem.

Parametryzacje działają na części powierzchni

Innym problemem jest to, że czasami powierzchnie nie mają parametryzacji, które obejmują całą powierzchnię; tak jest na przykład w przypadku powierzchni walca (o skończonej wysokości). Oczywistym rozwiązaniem jest wtedy podzielenie tej powierzchni na kilka kawałków, obliczenie całki powierzchniowej na każdym kawałku, a następnie zsumowanie ich wszystkich. Tak to rzeczywiście działa, ale przy całkowaniu pól wektorowych trzeba znów uważać, jak wybrać wektor normalny dla każdego kawałka powierzchni, tak by po złożeniu kawałków z powrotem wyniki były spójne. Dla walca oznacza to, że jeśli zdecydujemy, że dla obszaru bocznego normalna będzie wskazywać na zewnątrz ciała, to dla górnej i dolnej okrągłej części normalna również musi wskazywać na zewnątrz ciała.

Niespójne normale powierzchni

Wreszcie, istnieją powierzchnie, które nie mają normalnej powierzchniowej w każdym punkcie z konsekwentnymi wynikami (na przykład, pasek Möbiusa). Jeśli taka powierzchnia zostanie podzielona na kawałki, na każdym kawałku zostanie wybrana parametryzacja i odpowiadająca jej normalna powierzchniowa, a następnie kawałki te zostaną złożone z powrotem, to wektory normalne pochodzące z różnych kawałków nie mogą zostać pogodzone. Oznacza to, że na pewnym styku dwóch kawałków wektory normalne będą skierowane w przeciwnych kierunkach. Taką powierzchnię nazywamy nieorientowalną. Pola wektorowe nie mogą być całkowane na powierzchniach nieorientowalnych.

Powiązane strony

• Twierdzenie o rozbieżności
• Twierdzenie Stokesa
• Całka liniowa
• Całka objętościowa
• Kartezjański układ współrzędnych
• Elementy objętości i powierzchni w sferycznym układzie współrzędnych
• Elementy objętości i powierzchni w cylindrycznym układzie współrzędnych
• Metoda Holsteina-Herringa