AlegsaOnline.com

Walec (bryła) — definicja, rodzaje, pole powierzchni i objętość

Poznaj walec: definicja, rodzaje, wzory na pole powierzchni i objętość oraz praktyczne przykłady i obliczenia krok po kroku — wszystko jasno i zrozumiale.

Autor: Leandro Alegsa

03-04-2026

Walec jest jednym z najbardziej podstawowych zakrzywionych figur geometrycznych, z powierzchnią utworzoną przez punkty znajdujące się w stałej odległości od danego odcinka linii, znanego jako oś walca. Kształt ten można traktować jako graniastosłup kołowy. Zarówno powierzchnia jak i bryła utworzona wewnątrz może być nazywana walcem. Pole powierzchni i objętość walca są znane od czasów starożytnych.

W geometrii różniczkowej walec definiuje się szerzej jako dowolną powierzchnię foremną, która jest rozpięta przez jednoparametrową rodzinę prostych równoległych. Walec, którego przekrój jest elipsą, parabolą lub hiperbolą nazywamy odpowiednio walcem eliptycznym, walcem parabolicznym lub walcem hiperbolicznym.

Elementy walca

Podstawy – dwie przystające, równoległe figury (najczęściej koła) leżące w równoległych płaszczyznach.
Oś – odcinek łączący środki podstaw; dla walca prostego oś jest prostopadła do podstaw.
Wysokość (h) – odległość między płaszczyznami podstaw mierzona prostopadle do nich (dla walca pochyłego wysokość to odległość między płaszczyznami podstaw, niekoniecznie długość tworzącej).
Tworzące (generatry) – proste równoległe tworzące ścianę boczną walca; ich długość zwykle oznacza się przez l.
Promień podstawy (r) – w walcu kołowym odległość od środka podstawy do jej obwodu.

Rodzaje walców

Walec prosty (walec prawidłowy) – oś jest prostopadła do płaszczyzn podstaw; najczęściej rozważany przypadek walca kołowego.
Walec pochyły – oś nie jest prostopadła do podstaw; podstawy są przesunięte względem siebie.
Walec kołowy – podstawy są kołami (najczęściej wykorzystywany w zadaniach i praktyce).
Walce opisane w geometrii różniczkowej – np. walec eliptyczny, paraboliczny, hiperboliczny, gdy przekrój prostopadły do generatry jest odpowiednią krzywą.

Pole powierzchni walca

Dla walca kołowego o promieniu podstawy r i długości tworzącej l (w walcu prostym l = h) obowiązują wzory:

Pole powierzchni bocznej (Sc) = obwód podstawy × długość tworzącej = (2πr) × l = 2πr l.
Pole jednej podstawy (Sb) = π r².
Pole całkowite (St) = pole boczne + 2×pole podstawy = 2πr l + 2π r² = 2πr (r + l).

Uwagi:

Dla walca prostego l = h, więc pole boczne można zapisać jako 2πr h, a pole całkowite jako 2πr (r + h).
Interpretacja geometryczna: pole boczne walca prostego otrzymujemy rozwijając powierzchnię boczną – staje się prostokątem o wymiarach obwód podstawy (2πr) i wysokość h.
W walcu pochyłym zamiast h wstawia się długość tworzącej l (długość generatrix), bo rozwinięcie powierzchni bocznej daje prostokąt o wymiarach obwód podstawy × l.

Objętość walca

Dla walca o podstawie kołowej i wysokości h wzór na objętość jest prosty i wynika z zasady: objętość = pole podstawy × wysokość. Zatem

V = π r² h.

Uwaga: dla walca pochyłego objętość liczy się tak samo (ważna jest prostopadła odległość między płaszczyznami podstaw), co wynika z zasady Cavalieriego — jeżeli dwa walce mają równe wysokości i równe przekroje poprzeczne równoległe do podstaw to mają równe objętości.

Przykłady i zastosowania

Puszki, butelki, rury i kolumny są praktycznymi przykładami walców kołowych.
Przy obliczaniu ilości materiału potrzebnego na opakowanie używa się pola powierzchni; do obliczenia pojemności zbiornika — objętości.
Przykład obliczeniowy: dla walca o r = 3 cm i h = 5 cm: V = π·3²·5 = 45π cm³, Sc = 2π·3·5 = 30π cm², St = 2π·3(3+5) = 48π cm².

Dodatkowe uwagi

Terminologia: w literaturze spotyka się rozróżnienie między walcem jako powierzchnią (powłoka) i jako bryłą (wypełnionym wnętrzem). W zadaniach matematycznych zwykle chodzi o bryłę ograniczoną tymi powierzchniami.
W geometrii analitycznej walec można opisać równaniami; w przestrzeni R³ walec prosty o osi pokrywającej się z osią z i przekrojem kołowym ma równanie x² + y² = r² (niezależne od z).

Powszechne zastosowanie

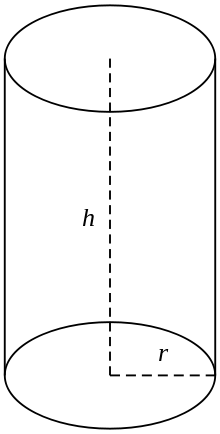
W powszechnym użyciu przez walec rozumie się skończony wycinek walca prostokątnego, tzn. walec o liniach generujących prostopadłych do podstaw, którego końce są zamknięte tak, że tworzą dwie powierzchnie kołowe, jak na rysunku (po prawej). Jeżeli walec ma promień $r$ i długość (wysokość) h, to jego objętość jest dana przez:

$V$ $= πr2h$

a jego powierzchnia wynosi:

powierzchnia wierzchołka $(πr2) +$
powierzchnia dna $(πr2) +$
obszar boku ( $2πrh$ ).

Dlatego bez góry i dołu (powierzchnia boczna), powierzchnia wynosi:

$A$ $= 2πrh$ .

Z górą i dołem, powierzchnia wynosi:

$A$ $= 2πr2 + 2πrh = 2πr(r + h)$ .

Dla danej objętości walec o najmniejszej powierzchni ma $h = 2r$ . Dla danej powierzchni walec o największej objętości ma $h = 2r$ , tzn. walec mieści się w sześcianie (wysokość = średnica).

Tom

Mając walec prostokątny o wysokości $h$ jednostek i podstawie o promieniu $r$ jednostek, którego osie współrzędnych są tak dobrane, że początek znajduje się w środku jednej z podstaw, a wysokość jest mierzona wzdłuż dodatniej osi x. Przekrój płaski w odległości $x jednostek$ od początku ma pole powierzchni $A (x)$ jednostek kwadratowych, gdzie

A ( x ) = π r 2 {{displaystyle A(x)=p r^{2}} $A(x)=\pi r^{2}$

lub

A ( y ) = π r 2 {{displaystyle A(y)={pi r^{2}} $A(y)=\pi r^{2}$

Elementem objętości jest prawy walec o polu podstawy $Awi$ jednostek kwadratowych i grubości Δix jednostek. Zatem jeśli V jednostek sześciennych jest objętością prawego walca kołowego, to na mocy sumy Riemanna,

V o l u m e o of c y l i n d e r = lim | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {displaystyle {Volume;of;cylinder} =lim _{||Delta \ do 0|} \sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {displaystyle = ∫ ∫ ∫ 0 h A ( y ) 2 d y {{0}^{h}A(y)^{2} } $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π r 2 d y {{displaystyle = ∫ 0 h π r 2 d y } $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {{displaystyle = \i0,r^{2} } $=\pi \,r^{2}\,h\,$

Używając współrzędnych cylindrycznych, objętość można obliczyć przez całkowanie po

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {displaystyle = ∫ 0 h ∫ 0 h ∫ 0 2 π ∫ 0 r s d ϕ d z } $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {{displaystyle = \i0,r^{2} } $=\pi \,r^{2}\,h\,$

Przekrój cylindryczny

Przekroje walcowe to przecięcia walców z płaszczyznami. Dla walca prostego kołowego istnieją cztery możliwości. Płaszczyzna styczna do walca styka się z nim w jednej prostej. Przesunięta równolegle do siebie płaszczyzna albo nie przecina walca, albo przecina go dwiema prostymi równoległymi. Wszystkie inne płaszczyzny przecinają walec w elipsie lub, gdy są prostopadłe do osi walca, w okręgu.

Inne rodzaje cylindrów

Walec eliptyczny, czyli cylindroid, jest powierzchnią czworokątną o następującym równaniu we współrzędnych kartezjańskich:

( x a )2 + ( y b )2 = 1. { {displaystyle \a_left({{frac {x}{a}}}}}prawica)^{2}+left({{frac {}{b}}}prawica)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Równanie to dotyczy walca eliptycznego, uogólnienia zwykłego walca kołowego ( $a = b$ ). Jeszcze bardziej ogólny jest walec uogólniony: jego przekrój może być dowolną krzywą.

Walec jest zdegenerowanym czworokątem, ponieważ co najmniej jedna ze współrzędnych (w tym przypadku $z$ ) nie występuje w równaniu.

Cylinder skośny ma górną i dolną powierzchnię przesuniętą względem siebie.

Istnieją jeszcze inne, bardziej niezwykłe rodzaje cylindrów. Są to wyimaginowane cylindry eliptyczne:

( x a ) 2 + ( y b ) 2 = - 1 { {displaystyle \left(\frac {x}{a}}}prawica)^{2}+ \left(\frac {}{b}}prawica)^{2}=-1}. $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

walec hiperboliczny:

( x a ) 2 - ( y b ) 2 = 1 { {displaystyle \frac {x}{a}}prawica} ^{2}- \frac {{b}prawica} ^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

i cylindra parabolicznego:

x 2 + 2 a y = 0. {displaystyle x^{2}+2ay=0.} $x^{2}+2ay=0.\,$

W geometrii rzutowej walec jest po prostu stożkiem, którego wierzchołek znajduje się w nieskończoności, co odpowiada wizualnie walcowi w perspektywie, który wydaje się być stożkiem w kierunku nieba.

Geometria rzutowa

W geometrii rzutowej walec to po prostu stożek, którego wierzchołek znajduje się w nieskończoności.

Jest to przydatne w definicji stożków zdegenerowanych, które wymagają rozważenia stożków walcowych.

Pytania i odpowiedzi

P: Co to jest walec?

O: Walec jest trójwymiarowym kształtem geometrycznym, którego powierzchnię tworzą punkty znajdujące się w stałej odległości od danego odcinka linii, zwanego osią walca. Można o nim myśleć jak o graniastosłupie kołowym i zarówno powierzchnię, jak i bryłę utworzoną wewnątrz można nazwać walcem.

P: Od jak dawna ludzie wiedzą o polu powierzchni i objętości walca?

O: Pole powierzchni i objętość cylindrów są znane od czasów starożytnych.

P: Co to jest walec eliptyczny, paraboliczny i hiperboliczny?

O: Cylindry eliptyczne, paraboliczne i hiperboliczne to cylindry, których przekrój poprzeczny jest odpowiednio elipsą, parabolą lub hiperbolą.

P: Jak definiuje się walec w geometrii różniczkowej?

O: W geometrii różniczkowej walec jest zdefiniowany szerzej jako powierzchnia ograniczona, która jest rozpięta przez jednoparametrową rodzinę linii równoległych.

P: Co to znaczy, że coś jest "rządzone"?

O: To, że coś jest "rządzone" oznacza, że ma narysowane linie proste w taki czy inny sposób.

P: Czy istnieje tylko jeden rodzaj walca?

O: Nie, istnieje wiele różnych rodzajów walców, takich jak eliptyczny, paraboliczny i hiperboliczny, które mają różne przekroje poprzeczne.