Okrąg
Koło to okrągły, dwuwymiarowy kształt. Wszystkie punkty na krawędzi okręgu znajdują się w tej samej odległości od środka.
Promień okręgu jest linią od środka okręgu do punktu na boku. Matematycy używają litery r dla długości promienia okręgu. Środkiem okręgu jest punkt znajdujący się na samym środku.
Średnica (czyli "w poprzek") okręgu jest linią prostą, która przechodzi z jednej strony na drugą i przez środek okręgu w prawo. Matematycy używają litery d dla długości tej linii. Średnica okręgu jest równa dwukrotnej wartości jego promienia (d równa się 2 razy r).
d = 2 r {\i1}displastyla d=2 r}
Obwód (oznaczający "całą drogę dookoła") okręgu jest linią, która biegnie dookoła jego środka. Matematycy używają litery C dla długości tej linii.
Liczba π (pisana jako grecka litera pi) jest bardzo użyteczną liczbą. Jest to długość obwodu podzielona przez długość średnicy (π równa się C podzielona przez d). Jako ułamek liczba π jest równa około 22⁄7 lub 335/113 (która jest bliższa) i jako liczba wynosi około 3,1415926535.
Obszar, a, wewnątrz okręgu jest równy promieniowi pomnożonemu przez siebie, a następnie pomnożonemu przez π (a równa się π razy r razy r).

Koło
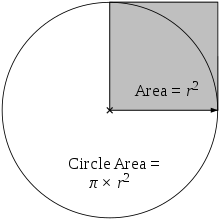
Powierzchnia koła jest równa π-krotności powierzchni szarego kwadratu.
Obliczanie π
π można zmierzyć poprzez narysowanie dużego okręgu, a następnie zmierzenie jego średnicy (d) i obwodu (C). Dzieje się tak, ponieważ obwód okręgu jest zawsze π razy większy od jego średnicy.
π = C d {\i1}Displaystyle \i0}pi {\i1}frac {\i1}{\i1}
π można również obliczyć tylko przy użyciu metod matematycznych. Większość metod stosowanych do obliczania wartości π ma pożądane właściwości matematyczne. Są one jednak trudne do zrozumienia bez znajomości trygonometrii i rachunku. Niektóre metody są jednak dość proste, jak na przykład ta forma serii Gregory-Leibniza:
Chociaż seria ta jest łatwa do napisania i obliczenia, nie jest łatwo zrozumieć, dlaczego jest równa π. Łatwiejszym do zrozumienia podejściem jest narysowanie wyimaginowanego okręgu o promieniu r wyśrodkowanym na początku. Wtedy każdy punkt (x,y), którego odległość d od początku jest mniejsza niż r, obliczony według twierdzenia Pitagorejczyka, znajdzie się wewnątrz okręgu:
d = x 2 + y 2 {\i1}displaystyle d={\i0}sqrt {x^{2}+y^{2}}}}}
Znalezienie zestawu punktów wewnątrz okręgu pozwala na oszacowanie obszaru A okręgu. Na przykład, używając współrzędnych całkowitych dla dużego r. Ponieważ obszar A okręgu jest π razy większy od kwadratu promienia, π można przybliżyć za pomocą:
π = A r 2 {\i1}displaystyle \i0}pi ={\i1}frac {\i1}{r^{\i1}COPY0
Powiązane strony
- Sfera
Pytania i odpowiedzi
P: Co to jest koło?
O: Koło jest okrągłym, dwuwymiarowym kształtem. Wszystkie punkty na brzegu okręgu znajdują się w tej samej odległości od środka.
P: Czego matematycy używają, aby przedstawić długość promienia okręgu?
O: Matematycy używają litery r dla określenia długości promienia okręgu.
P: Co jest zapisywane jako O w okręgach?
O: Środek okręgu jest często zapisywany jako O.
P: Jak długa jest średnica koła?
O: Średnica (czyli "cała długość") koła to linia prosta, która przechodzi z jednego boku na drugi i prosto przez środek koła. Jest ona równa dwukrotności promienia (d równa się 2 razy r).
P: Jaką literą matematycy oznaczają obwód?
O: Matematycy używają litery C dla obwodu, co oznacza "dookoła".
P: Jak obliczyć pole powierzchni wewnątrz koła?
A: Pole powierzchni, A, wewnątrz okręgu można obliczyć, mnożąc jego promień przez siebie, a następnie mnożąc przez ً (A równa się ً razy r razy r).
Przeszukaj encyklopedię



