Pi

Pi (lub π) jest stałą matematyczną. Jest to stosunek odległości wokół okręgu do jego średnicy. W ten sposób powstaje liczba, która zawsze jest taka sama. Jednak liczba ta jest dość dziwna. Zaczyna się od 3,141592653589793... i ciągnie się bez końca. Liczby takie jak ta nazywane są liczbami irracjonalnymi.

Średnica jest największą cięciwą, która może być umieszczona wewnątrz okręgu. Przechodzi ona przez środek okręgu. Odległość wokół okręgu nazywana jest obwodem. Nawet jeśli średnica i obwód są różne dla różnych okręgów, liczba pi pozostaje stała: jej wartość nigdy się nie zmienia. Dzieje się tak dlatego, że związek między obwodem a średnicą jest zawsze taki sam.

π = C d {{displaystyle \i ={frac {C}{d}}} $\pi ={\frac {C}{d}}$ (pi jest równe obwodowi podzielonemu przez średnicę).

Pi to niekończący się ciąg liczb

Aproksymacja

Pi jest często zapisywana formalnie jako $π$ lub grecka litera π jako skrót. Pi jest również liczbą irracjonalną, co oznacza, że nie może być zapisana jako ułamek ( a b {{displaystyle a \over b}} $a \over b$ ), gdzie "a" i "b" są liczbami całkowitymi (całymi). Oznacza to w zasadzie, że cyfry pi, które znajdują się na prawo od liczby dziesiętnej, nie powtarzają się w żaden sposób i że niemożliwe jest zapisanie dokładnej wartości pi jako liczby. Pi może być jedynie przybliżone lub zmierzone do wartości, która jest wystarczająco bliska dla celów praktycznych.

Wartość zbliżona do pi to 3,141592653589793238462643... Popularnym przybliżeniem ułamka pi jest 22 7 {displaystyle 22 \u0026apos; 7}. $22 \over 7$ , co daje w przybliżeniu 3,14285714. Przybliżenie to jest o 0,04% oddalone od prawdziwej wartości pi. Podczas gdy to przybliżenie jest akceptowane dla większości jego zastosowań w prawdziwym życiu, ułamek 355 113 {displaystyle 355 \over 113} $355 \over 113$ jest dokładniejszy (dając około 3,14159292) i może być używany, gdy potrzebna jest wartość bliższa pi. Komputery mogą być używane do uzyskiwania lepszych przybliżeń liczby pi.

W marcu 2019 roku Emma Haruka Iwao obliczyła wartość liczby pi na 31,4 biliona cyfr.

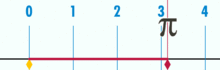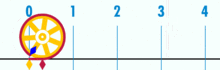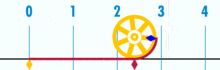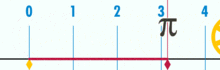
Diagram pokazuje, że π można znaleźć za pomocą okręgu o średnicy równej jeden. Obwód tego okręgu wynosi π.

Historia

Wartość pi była znana starożytnym matematykom indyjskim, takim jak Bhaskaracharya i Aryabhatta.

Matematycy wiedzą o liczbie pi od tysięcy lat, ponieważ przez tyle samo czasu zajmowali się okręgami. Cywilizacje tak stare jak Babilończycy były w stanie przybliżyć pi do wielu cyfr, takich jak ułamek 25/8 i 256/81. Większość historyków uważa, że starożytni Egipcjanie nie mieli pojęcia π i że ta zgodność jest przypadkowa.

Pierwsze pisemne odniesienie do liczby pi datuje się na rok 1900 p.n.e. Około 1650 r. p.n.e. egipski Ahmes podał wartość w papirusie Rhind. Babilończycy byli w stanie ustalić, że wartość pi jest nieco większa niż 3, po prostu robiąc duże koło, a następnie przyklejając kawałek liny na obwodzie i średnicy, notując ich odległości, a następnie dzieląc obwód przez średnicę.

Wiedza o liczbie pi wróciła do Europy i trafiła w ręce Hebrajczyków, dla których liczba ta stała się ważna w części Biblii zwanej Starym Testamentem. Później najczęstszym sposobem znalezienia liczby pi było narysowanie kształtu o wielu bokach wewnątrz dowolnego okręgu i wykorzystanie pola tego kształtu do znalezienia liczby pi. Grecki filozof Archimedes, na przykład, użył kształtu wielokąta, który miał 96 boków, aby znaleźć wartość pi, ale Chińczycy w 500 CE byli w stanie użyć wielokąta o 16,384 bokach, aby znaleźć wartość pi. Grecy, tacy jak Anaksagoras z Clazomenae, byli również zajęci odkrywaniem innych własności okręgu, takich jak tworzenie kwadratów z okręgów i kwadratura liczby pi. Od tego czasu wielu ludzi próbowało znaleźć coraz dokładniejsze wartości liczby pi.

Historia pi
Filozof	Data	Aproksymacja
Klaudiusz Ptolemeusz	około 150 r. n.e.	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	około 800 r. n.e.	3.1416
al-Kashi	około 1430 r.	3.14159265358979
Viète	1540–1603	3.141592654
Roomen	1561–1615	3.14159265358979323
Van Ceulen	około 1600	3.14159265358979323846264338327950288

W XVI wieku pojawiły się coraz lepsze sposoby na znalezienie liczby pi, takie jak skomplikowany wzór, który opracował francuski prawnik François Viète. Po raz pierwszy grecki symbol "π" został użyty w eseju napisanym w 1706 roku przez Williama Jonesa.

Matematyk o nazwisku Lambert wykazał również w 1761 roku, że liczba pi jest irracjonalna, to znaczy, że nie może być zapisana jako ułamek w normalnych standardach. Inny matematyk o nazwisku Lindeman był również w stanie wykazać w 1882 roku, że pi jest częścią grupy liczb znanych jako transcendentale, które są liczbami, które nie mogą być rozwiązaniem równania wielomianowego.

Pi może być również używane do określania wielu innych rzeczy poza okręgami. Właściwości liczby pi pozwoliły na jej wykorzystanie w wielu innych dziedzinach matematyki poza geometrią, która bada kształty. Niektóre z tych dziedzin to analiza złożona, trygonometria i serie.

Pi w realu

Obecnie istnieją różne sposoby obliczania wielu cyfr liczby π. Ich zastosowanie jest jednak ograniczone.

Pi można czasem wykorzystać do obliczenia pola powierzchni lub obwodu dowolnego okręgu. Aby znaleźć obwód okręgu, skorzystaj ze wzoru C (obwód) = π razy średnica. Aby znaleźć pole koła, należy skorzystać ze wzoru π (promień²). Wzór ten jest czasem zapisywany jako A = π r 2 {{displaystyle A= r^{2}} $A=\pi r^{2}$ gdzie r jest zmienną określającą promień okręgu, a A jest zmienną określającą pole tego okręgu.

Obliczyć obwód okręgu z błędem 1 mm:

Dla promienia 30 metrów potrzebne są 4 cyfry
10 cyfr dla promienia równego promieniowi Ziemi
15 cyfr dla promienia równego odległości od Ziemi do Słońca.

Ludzie zazwyczaj obchodzą 14 marca jako Dzień Liczby Pi, ponieważ 14 marca jest również zapisywany jako 3/14, co reprezentuje trzy pierwsze cyfry 3,14 w przybliżeniu liczby pi. Dzień Liczby Pi rozpoczął się w 2001 roku.

Powiązane strony

Koło

Pytania i odpowiedzi

P: Co to jest liczba ً?

A: ً to stała matematyczna, która jest stosunkiem obwodu koła do jego średnicy.

P: Co to daje?

O: Powstaje liczba, a ta liczba jest zawsze taka sama.

P: Jak zaczyna się ta liczba?

O: Liczba zaczyna się od 3,141592653589793... i trwa bez końca.

P: Jakiego rodzaju są to liczby?

O: Te liczby są nazywane liczbami irracjonalnymi.

P: Jaka jest średnica koła?

A: Średnica koła to największa cięciwa, jaką można zmieścić w jego wnętrzu, przechodząca przez jego środek.
P: Co to jest obwód koła? A: Odległość wokół koła nazywamy jego obwodem.

P: Czy pi pozostaje stałe niezależnie od różnych okręgów? O: Tak, pi pozostaje stałe niezależnie od różnych okręgów, ponieważ stosunek ich obwodu do średnicy zawsze pozostaje taki sam.