Skala logarytmiczna
Skala logarytmiczna jest skalą stosowaną w przypadku dużego zakresu wielkości. Powszechnie używa się jej do określenia wytrzymałości na trzęsienia ziemi, głośności dźwięku, natężenia światła i pH roztworów.
Jest on oparty na rzędach wielkości, a nie na standardowej skali liniowej. Wartość każdego znaku na skali jest wartością na poprzednim znaku pomnożoną przez stałą.
Skale logarytmiczne są również używane w suwakach do mnożenia lub dzielenia liczb poprzez dodawanie lub odejmowanie długości na skali.
Skala logarytmiczna może być pomocna, gdy dane obejmują duży zakres wartości - logarytm redukuje to do bardziej przystępnego zakresu.
Niektóre z naszych zmysłów działają w sposób logarytmiczny (pomnożenie rzeczywistej siły wejściowej dodaje stałą do postrzeganej siły sygnału, patrz: prawo mocy Stevensa). To sprawia, że skale logarytmiczne dla tych wielkości wejściowych są szczególnie odpowiednie. W szczególności, nasz zmysł słuchu odbiera równe wielokrotności częstotliwości jako równe różnice w wysokości dźwięku.
Na większości skal logarytmicznych, małe wielokrotności (lub proporcje) wielkości bazowej odpowiadają małym (możliwie ujemnym) wartościom miary logarytmicznej.
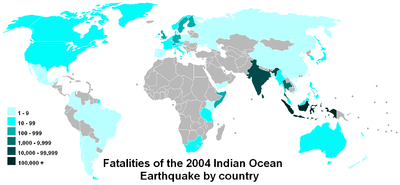
Skala logów ułatwia porównywanie wartości, które obejmują duży zakres, jak na przykład w tej mapie
Dwie skale logarytmiczne suwmiarki
Przykłady
Dobrze znanymi przykładami takich wag są:
- Bogatsza skala magnitudowa i skala chwilowa (MMS) dla siły trzęsień ziemi i ruchu w ziemi.
- bel i decybel i neper dla mocy akustycznej (głośności) i mocy elektrycznej;
- liczenie f-stopni dla współczynników ekspozycji fotograficznej;
- oceniając niskie prawdopodobieństwa za pomocą liczby "dziewiątek" w dziesiętnych rozwinięciach prawdopodobieństwa ich nie wystąpienia: na przykład system, który zawiedzie z prawdopodobieństwem 10-5, jest wiarygodny w 99,999%: "pięć dziewiątek".
- Entropia w termodynamice.
- Informacje w teorii informacji.
- Krzywe rozkładu wielkości cząstek gleby
Niektóre skale logarytmiczne zostały zaprojektowane tak, aby duże wartości (lub proporcje) wielkości bazowej odpowiadały małym wartościom miary logarytmicznej. Przykładami takich skal są:
- pH dla kwasowości;
- gwiezdna skala wielkości dla jasności gwiazd;
Skala logarytmiczna to również skala graficzna na jednej lub obu stronach wykresu, gdzie liczba x jest drukowana w odległości c-log(x) od punktu oznaczonego liczbą 1. Suwak logarytmiczny posiada skale logarytmiczne, a nomogramy często wykorzystują skale logarytmiczne. Na skali logarytmicznej różnica rzędu wielkości jest reprezentowana przez równą odległość. Średnia geometryczna dwóch liczb znajduje się w połowie odległości między nimi.
Papier do grafów logarytmicznych, przed pojawieniem się grafiki komputerowej, był podstawowym narzędziem naukowym. Wykresy na papierze z jedną skalą logarytmiczną mogą przedstawiać prawa wykładnicze, a na papierze logarytmicznym prawa mocy, jako linie proste (patrz wykres półilogowy, wykres logarytmiczny).
Pytania i odpowiedzi
Q: Co to jest skala logarytmiczna?
O: Skala logarytmiczna to skala używana w przypadku dużego zakresu wielkości.
P: Jakie są przykłady rzeczy, które można mierzyć w skali logarytmicznej?
O: Siła trzęsienia ziemi, głośność dźwięku, natężenie światła, szybkość rozprzestrzeniania się epidemii i pH roztworów mogą być mierzone w skali logarytmicznej.
P: Czym różni się skala logarytmiczna od standardowej skali liniowej?
O: Skala logarytmiczna opiera się na rzędach wielkości, a nie na standardowej skali liniowej. Wartość każdego znaku na skali to wartość poprzedniego znaku pomnożona przez stałą.
P: Jaka jest korzyść z używania skali logarytmicznej?
O: Skala logarytmiczna może zredukować duży zakres wartości do łatwiejszego w zarządzaniu zakresu, co może być pomocne w przypadku danych obejmujących szeroki zakres wartości.
P: Co to jest prawo potęgowe Stevensa i jaki ma związek ze skalą logarytmiczną?
O: Prawo mocy Stevensa opisuje, w jaki sposób niektóre z naszych zmysłów działają w sposób logarytmiczny, gdzie mnożenie rzeczywistej siły wejściowej dodaje stałą do postrzeganej siły sygnału. To sprawia, że skale logarytmiczne dla tych wielkości wejściowych są szczególnie odpowiednie.
P: Dlaczego skala logarytmiczna jest szczególnie przydatna do pomiaru głośności dźwięku?
O: Nasz zmysł słuchu postrzega równe wielokrotności częstotliwości jako równe różnice w wysokości dźwięku, więc skala logarytmiczna może dokładnie reprezentować tę zależność między częstotliwością dźwięku a postrzeganą głośnością.
P: Jaki jest związek między małymi wielokrotnościami wielkości bazowej a miarą logarytmiczną w większości skal logarytmicznych?
O: W większości skal logarytmicznych małe wielokrotności (lub proporcje) wielkości bazowej odpowiadają małym (ewentualnie ujemnym) wartościom miary logarytmicznej.
Przeszukaj encyklopedię