Nomogram
Nomogram lub wykres wyrównawczy lub abaque, jest wykresem obliczeniowym. Jest to dwuwymiarowy diagram, który podaje obliczenie funkcji matematycznej.
Dziedzina nomografii została wynaleziona w 1884 roku przez francuskiego inżyniera Philberta Maurice d'Ocagne (1862-1938). Przez wiele lat służyła inżynierom do szybkich obliczeń graficznych skomplikowanych wzorów. Nomogramy wykorzystują równoległy układ współrzędnych wynaleziony przez d'Ocagne'a zamiast standardowych współrzędnych kartezjańskich.
Nomogram składa się z zestawu n skal, po jednej dla każdej zmiennej w równaniu. Znając wartości n-1 zmiennych można znaleźć wartość zmiennej nieznanej lub ustalając wartości niektórych zmiennych można badać zależności między zmiennymi nie ustalonymi.
Wynik otrzymuje się poprzez położenie liniału prostego w poprzek znanych wartości na skalach i odczytanie nieznanej wartości z miejsca, w którym przecina on skalę dla danej zmiennej. Wirtualna lub narysowana linia utworzona przez linijkę jest nazywana linią wskaźnikową lub izopletą.
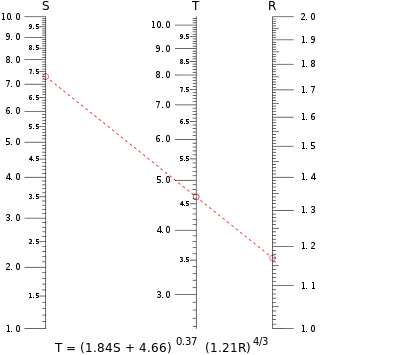
Typowy nomogram w skali równoległej. Ten przykład oblicza wartość T, gdy S = 7,30 i R = 1,17 są podstawione do równania. Izopleta przecina skalę dla T na poziomie nieco poniżej 4,65.
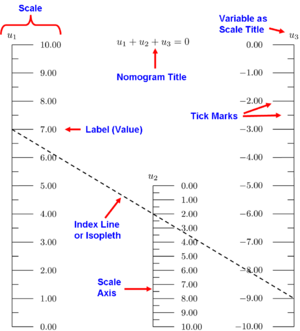
Części składowe nomogramu w skali równoległej
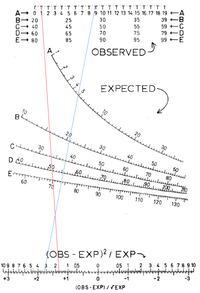
Nomogram rozkładu Chi-kwadrat
Użyj
Nomogramy były powszechnie stosowane przez około 75 lat. Pozwalały na szybkie i dokładne obliczenia przed erą kieszonkowych kalkulatorów. Wyniki z nomogramu otrzymuje się szybko i niezawodnie przez narysowanie jednej lub kilku linii. Użytkownik nie musi wiedzieć, jak rozwiązywać równania algebraiczne, szukać danych w tabelach, używać suwaka logarytmicznego lub podstawiać liczby do równań, aby uzyskać wyniki. Użytkownik nie musi nawet znać podstawowego równania, które nomogram reprezentuje.
Nomogramy zawierają w swojej konstrukcji wiedzę z danej dziedziny. Na przykład, aby stworzyć większe nomogramy dla większej dokładności, nomograf zazwyczaj uwzględnia tylko te zakresy skali, które są rozsądne i interesujące dla danego problemu. Wiele nomogramów zawiera inne użyteczne oznaczenia, takie jak etykiety referencyjne i kolorowe regiony. Wszystkie te elementy stanowią użyteczne drogowskazy dla użytkownika.
Podobnie jak suwak logarytmiczny, nomogram jest graficznym analogowym urządzeniem obliczeniowym. Podobnie jak suwak logarytmiczny, jego dokładność jest ograniczona przez precyzję, z jaką można narysować, odtworzyć, obejrzeć i wyrównać fizyczne oznaczenia. Suwak logarytmiczny jest kalkulatorem ogólnego przeznaczenia, ale nomogram jest przeznaczony do wykonywania konkretnych obliczeń. Nomogramy mogą być nadal używane do sprawdzania odpowiedzi z innego, bardziej dokładnego, ale prawdopodobnie podatnego na błędy obliczenia.
Pytania i odpowiedzi
P: Co to jest nomogram?
O: Nomogram to wykres używany do obliczeń, który przedstawia obliczenia funkcji matematycznej.
P: Kto wymyślił dziedzinę nomografii?
O: Dziedzina nomografii została wynaleziona przez Philberta Maurice'a d'Ocagne, francuskiego inżyniera, w 1884 roku.
P: Jaki był cel nomogramów?
O: Nomogramy były używane przez wiele lat w celu zapewnienia inżynierom szybkich obliczeń graficznych skomplikowanych wzorów.
P: Z ilu skal składa się nomogram?
O: Nomogram składa się z zestawu n skal, po jednej dla każdej zmiennej w równaniu.
P: W jaki sposób można znaleźć wartość nieznanej zmiennej za pomocą nomogramu?
O: Znając wartości n-1 zmiennych, wartość nieznanej zmiennej można znaleźć, kładąc prostą krawędź w poprzek znanych wartości na skalach i odczytując nieznaną wartość z miejsca, w którym przecina skalę dla tej zmiennej.
P: Jak nazywa się wirtualna lub narysowana linia utworzona przez linijkę?
O: Wirtualna lub narysowana linia utworzona przez linijkę nazywana jest linią indeksu lub izopletą.
P: Jaki układ współrzędnych jest używany w nomogramach?
O: Nomogramy wykorzystują równoległy układ współrzędnych wynaleziony przez d'Ocagne'a zamiast standardowych współrzędnych kartezjańskich.
