Szereg harmoniczny

W matematyce serie harmoniczne są rozbieżnymi, nieskończonymi seriami:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\i1} {\i1} {\i1}{\i1}^{\i1}{\i1}{\i1}=1+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1} $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Rozbieżne oznacza, że gdy dodasz więcej terminów, suma nigdy nie przestanie się powiększać. Nie idzie ona w kierunku jednej skończonej wartości.

Infinite oznacza, że zawsze można dodać kolejny termin. Nie ma żadnego terminu końcowego do serii.

Jego nazwa pochodzi od idei harmonicznych w muzyce: długość fali podtekstów wibrującej struny wynosi 1/2, 1/3, 1/4 itd. podstawowej długości fali struny. Oprócz pierwszego członu, każdy człon serii jest średnią harmoniczną członów z każdej strony. Wyrażenie średnia harmoniczna pochodzi również z muzyki.

Historia

O tym, że serie harmoniczne są rozbieżne, po raz pierwszy udowodniła to Nicole Oresme w XIV wieku, ale o tym zapomniała. Dowody zostały podane w XVII wieku przez Pietro Mengoli, Johanna Bernoulli i Jacoba Bernoulli.

Sekwencje harmoniczne zostały wykorzystane przez architektów. W okresie baroku architekci wykorzystywali je w proporcjach rzutów kondygnacji, elewacji oraz w relacjach między detalami architektonicznymi kościołów i pałaców.

Dywergencja

Istnieje kilka znanych dowodów na rozbieżność serii harmonicznych. Kilka z nich podano poniżej.

Test porównawczy

Jednym ze sposobów na udowodnienie rozbieżności jest porównanie serii harmonicznych z innymi rozbieżnymi seriami, w których każdy mianownik jest zastępowany przez następny co do wielkości moc dwóch:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\i1}styk stylistyczny {\i1}&{}1+{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}+{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}&1+{frac {1}{2}+{frac {1}{color {czerwony}{mathbf {4} {y:i}++frac {1}{4}+frac {1}{color {czerwony}{mathbf {8} {y:i}++frac {1}{8}+frac {1}{color {czerwony}{mathbf {16} {y:i}+cdots {y:i}end {y:i}alignededed} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Każdy termin szeregu harmonicznego jest większy lub równy odpowiadającemu mu terminowi drugiego szeregu, a zatem suma szeregów harmonicznych musi być większa lub równa sumie terminów drugiego szeregu. Suma drugich szeregów jest jednak nieskończona:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\i1+ \i1+ \i1+ lewa(frac {\i0}{\i1}prawda)\i0+lewa(frac {\i0}{\i1})!+\W prawo! W lewo!+\W porządku, lewa strona!{frac {1}{16} {cdots} {y:i}&1+{frac {1}{2}+{frac {1}{2}}+{frac {1}{2}{frac {2}{cdots}+{frac {1}{2}{cdots}{cdots}{infract {1}{\i1} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Wynika z tego (poprzez test porównawczy), że suma szeregów harmonicznych musi być również nieskończona. Dokładniej mówiąc, powyższe porównanie dowodzi, że

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\i1} {\i1} {\i1}^{\i1}{\i1}{\i1}{\i1}frac {\i1}{\i1}}geq 1+{\i1}frac {\i1}{\i1}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

dla każdej dodatniej liczby całkowitej $k$ .

Dowód ten, zaproponowany przez Nicole Oresme około 1350 roku, uważany jest za wysoki punkt w matematyce średniowiecznej. Do dziś jest to standardowy dowód nauczany na lekcjach matematyki.

Test integralny

Można udowodnić, że szeregi harmoniczne różnią się od siebie poprzez porównanie ich sumy z niewłaściwą całką. Należy zwrócić uwagę na układ prostokątów pokazany na rysunku po prawej stronie. Każdy z prostokątów ma 1 jednostkę szerokości i 1/n jednostek wysokości, a więc całkowita powierzchnia nieskończonej liczby prostokątów jest sumą szeregów harmonicznych:

Całkowita powierzchnia pod krzywą $y =$ 1/x od 1 do nieskończoności jest podana przez rozbieżną, niewłaściwą całkę:

obszar pod krzywą = ∫ 1 ∞ 1 x d x = ∞ . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Ponieważ obszar ten w całości mieści się w obrębie prostokątów, łączna powierzchnia prostokątów musi być również nieskończona. Dowodzi to, że

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\i1}Displaystyle \i1}{\i1}^{\i1}{\i1}{\i1}{\i1}{\i1}, dx=ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Uogólnienie tego argumentu znane jest jako test integralny.

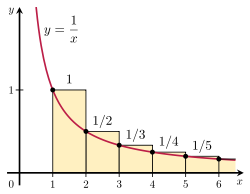
Ilustracja testu integralnego.

Stopa rozbieżności

Serie harmoniczne rozchodzą się bardzo powoli. Na przykład, suma pierwszych ¹⁰⁴³ terminów wynosi mniej niż 100. Dzieje się tak, ponieważ częściowe sumy szeregów mają wzrost logarytmiczny. W szczególności,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\i1}styk stylistyczny _{n=1}^{\i1}{\i1}{\i1}{\i1}= ln k+gamma +\i0}varepsilon _{\i0}leq (ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

gdzie γ jest stałą Eulera-Mascheroniego, a εk $~$ 1/2k, która zbliża się do 0 jak $k$ idzie w nieskończoność. Leonhard Euler udowodnił zarówno to, jak i to, że suma, która zawiera tylko odwrotności pierwiastków pierwotnych również się różni, czyli:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Kwoty częściowe

Pierwsza trzydziestka liczb harmonicznych
$n$	Częściowa suma serii harmonicznych, $Hn$
$n$	wyrażony jako ułamek		z dokładnością do jednego miejsca po przecinku	względny rozmiar
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Skończone częściowe sumy rozbieżnych serii harmonicznych,

H n = ∑ k = 1 n 1 k , {\i1}==sum _{k=1}^{\i1}{\i1}frac {\i1}{\i1},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

są nazywane numerami harmonicznymi.

Różnica między $Hn$ i $ln n$ zbiega się ze stałą Euler-Mascheroni. Różnica pomiędzy dwoma dowolnymi liczbami harmonicznymi nigdy nie jest liczbą całkowitą. Żadne liczby harmoniczne nie są liczbami całkowitymi, z wyjątkiem $H1 = 1$ .

Powiązane serie

Zmienne szeregi harmoniczne

Seria

znana jest jako naprzemienna seria harmoniczna. Seria ta jest zbieżna w teście serii naprzemiennych harmonicznych. W szczególności, suma jest równa logarytmowi naturalnemu 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2.

Zmienna seria harmoniczna, podczas gdy warunkowo zbieżna, nie jest absolutnie zbieżna: jeśli terminy w serii są systematycznie zmieniane, w ogóle suma staje się inna i, w zależności od zmiany układu, może nawet nieskończona.

Wzór na zmienne szeregi harmoniczne jest specjalnym przypadkiem serii Mercator, serii Taylor dla logarytmu naturalnego.

Powiązana seria może być wyprowadzona z serii Taylora dla arktangantu:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1}-{\i1} } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

To jest znane jako seria Leibniza.

Ogólne serie harmoniczne

Ogólna seria harmoniczna jest w formie

∑ n = 0 ∞ 1 a n + b , {\i0}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

gdzie $a \neq 0$ i $b$ są liczbami rzeczywistymi, a b/a nie jest zerem lub liczbą całkowitą ujemną.

Poprzez test porównawczy z seriami harmonicznymi, wszystkie ogólne serie harmoniczne również się różnią.

$p-seria$

Uogólnienie serii harmonicznych to seria $p$ (lub seria hiperharmoniczna), zdefiniowana jako

∑ n = 1 ∞ 1 n p {\i1} {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}frac {\i1}{\i1}{\i1}n^}}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

dla każdej liczby rzeczywistej $p$ . Gdy $p = 1$ , $seria p$ jest serią harmoniczną, która jest rozbieżna. Test całkowania lub test kondensacji Cauchy'ego pokazuje, że seria $p jest zbieżna$ dla wszystkich $p > 1 ($ w tym przypadku nazywana jest serią nadharmoniczną) i różni się dla wszystkich p $\leq 1.$ Jeżeli $p > 1$ , to suma szeregów p wynosi ζ( $p), tzn.$ funkcja Riemanna zeta oceniona na p.

Problem znalezienia sumy dla $p = 2 nazywany jest$ problemem bazylejskim; Leonhard Euler pokazał, że jest to π2/6. Wartość sumy dla $p = 3 nazywana jest$ stałą Apéry'ego, ponieważ Roger Apéry udowodnił, że jest to liczba nieracjonalna.

ln-seria

W odniesieniu do $serii p$ jest to seria ln, zdefiniowana jako

∑ n = 2 ∞ 1 n ( ln n ) p {\i1}displaystyle \i0}sum _{n=2}^ {\i1}infrac {\i1}{n(\i0} n)^(p}}}}) $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

dla każdej dodatniej liczby rzeczywistej $p$ . Można to wykazać testem integralnym, aby odbiegać od siebie dla $p \leq 1$ , ale zbiegać się dla wszystkich $p > 1.$

$φ-seria$

Dla każdej wypukłej, rzeczywistej funkcji φ takiej, że

lim {y:i}sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {y:i}displaystyle {y:i}limsup _{u`to 0^{+}{\i1}{\i1}frac {\i1}varphi {\i0}left(\i0}{\i1}{\i1}prawda){\i0} {\i1}, {\i1} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

seriale

∑ n = 1 ∞ φ φ ( 1 n ) {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1} {\i1}varphi {\i1} {\i1}Lewy{\i1} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

jest zbieżny. ^[]

Serie harmoniczne losowe

Losowa seria harmoniczna

∑ n = 1 ∞ s n n , {\i1} {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

gdzie $sn$ są niezależne, identycznie rozmieszczone zmienne losowe przyjmujące wartości +1 i -1 z równym prawdopodobieństwem 1/2, jest znanym przykładem w teorii prawdopodobieństwa dla serii zmiennych losowych, które zbiegają się z prawdopodobieństwem 1. Fakt tej zbieżności jest łatwą konsekwencją albo twierdzenia Kołmogorowa o trzech seriach, albo ściśle związanej z nim maksymalnej nierówności Kołmogorowa. Byron Schmuland z Uniwersytetu Alberta zbadał dalej właściwości serii harmonicznych losowych i wykazał, że seria zbieżna jest zmienną losową o kilku interesujących właściwościach. W szczególności funkcja gęstości prawdopodobieństwa tej zmiennej losowej oceniana na +2 lub na -2 przyjmuje wartość 0,1249999999999999999999999999999999999999764..., różniącą się od 1/8 o mniej niż 10-42. Praca Schmulanda wyjaśnia, dlaczego to prawdopodobieństwo jest tak bliskie, ale nie do końca, 1/8. Dokładna wartość tego prawdopodobieństwa jest podana przez nieskończoną cosinusoidalną całkę produktu $C2$ podzieloną przez π.

Wyczerpane serie harmoniczne

Wyczerpany szereg harmoniczny, w którym wszystkie terminy, w których cyfra 9 pojawia się gdziekolwiek w mianowniku, są usunięte, może być pokazany jako zbieżny, a jego wartość jest mniejsza niż 80. W rzeczywistości, gdy wszystkie terminy zawierające dowolny ciąg cyfr (w dowolnej bazie) są usunięte, seria ta jest zbieżna.

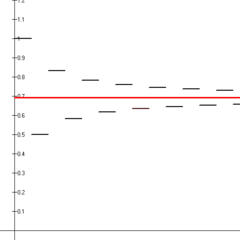
Pierwsze czternaście częściowych sum zmiennych serii harmonicznych (czarne odcinki linii) wykazuje zbieżność z logarytmem naturalnym 2 (czerwona linia).

Aplikacje

Serie harmoniczne mogą być przeciwintuicyjne. Dzieje się tak dlatego, że jest to seria rozbieżna, mimo że warunki serii stają się mniejsze i idą w kierunku zera. Dywergencja szeregów harmonicznych jest źródłem pewnych paradoksów.

"Robak na gumce". Załóżmy, że ślimak czołga się wzdłuż nieskończenie elastycznej jednometrowej gumki w tym samym czasie, gdy gumka jest równomiernie rozciągnięta. Jeśli ślimak porusza się z prędkością 1 centymetra na minutę, a taśma naciąga się z prędkością 1 metra na minutę, to czy ślimak kiedykolwiek dotrze do końca gumki? Odpowiedź, wbrew pozorom, brzmi "tak", ponieważ po $n$ minutach stosunek odległości pokonanej przez ślimaka do całkowitej długości gumki wynosi

1 100 ∑ k = 1 n 1 k . {\i1}{\i1}{\i1}{C:$aaccff}{c:$aaccff}{\i1}{c:$aaccff}{\i1}{c:$aaccff}{\i1}{\i1}{\i1}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Ponieważ seria staje się arbitralnie duża, gdy $n$ staje się większa, ostatecznie stosunek ten musi przekraczać 1, co oznacza, że ślimak osiąga koniec gumy. Jednak wartość $n$ , przy której to następuje, musi być bardzo duża: około e100, czyli liczba przekraczająca ¹⁰⁴³ minuty (1037 lat). Mimo, że szeregi harmoniczne są rozbieżne, to jednak robią to bardzo powoli.

Problem z Jeepem dotyczy tego, ile paliwa potrzeba do przejechania przez pustynię samochodu o ograniczonej ładowności, pozostawiając po sobie spadki paliwa na trasie. Odległość, jaką samochód może pokonać z daną ilością paliwa, jest związana z częściowymi sumami serii harmonicznych, które rosną logarytmicznie. I tak potrzebne paliwo rośnie wykładniczo wraz z wymaganą odległością.

Problem układania blokowego: biorąc pod uwagę kolekcję identycznych domino, możliwe jest układanie ich na brzegu stołu tak, aby wisiały nad krawędzią stołu, nie spadając. Wbrew pozorom można je układać w taki sposób, aby zwisały na krawędzi stołu, nie spadając. To znaczy, pod warunkiem, że jest wystarczająco dużo domino.

Pływak, który idzie szybciej za każdym razem, gdy dotykają ściany basenu. Pływak rozpoczyna przeprawę przez 10-metrowy basen z prędkością 2 m/s, a przy każdym przejściu dodawane są kolejne 2 m/s do prędkości. Teoretycznie prędkość pływaka jest nieograniczona, ale liczba przejazdów w basenie potrzebnych do osiągnięcia tej prędkości staje się bardzo duża; na przykład, aby dostać się do prędkości światła (ignorując szczególną względność), pływak musi przejść przez basen 150 milionów razy. W przeciwieństwie do tej dużej liczby, czas potrzebny do osiągnięcia danej prędkości zależy od sumy serii przy danej liczbie krzyżyków w basenie:

10 2 ∑ k = 1 n 1 k . {\i1}{\i1}{\i1}{\i1}{C:$aaccff}{c:$aaccff}{\i1}{c:$aaccff}{\i1}{c:$aaccff}{\i1}{\i1}.../ } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Obliczenie sumy pokazuje, że czas potrzebny do osiągnięcia prędkości światła wynosi tylko 97 sekund.

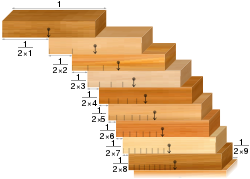
Problem układania bloków: bloki ułożone zgodnie z szeregiem harmonicznym mostkują rozszczepy o dowolnej szerokości.

Powiązane strony

Harmonijny postęp
Wykaz kwot wzajemnych rozliczeń

Pytania i odpowiedzi

P: Co to jest szereg harmoniczny?

O: Szereg harmoniczny jest nieskończonym szeregiem rozbieżnym, w którym każdy człon jest równy 1 podzielonemu przez jego pozycję w ciągu.

P: Co to znaczy, że szereg jest rozbieżny?

O: Rozbieżność oznacza, że w miarę dodawania kolejnych członów, suma nie przestaje się powiększać i nie zmierza do jednej skończonej wartości.

P: Co to znaczy, że szereg jest nieskończony?

O: Nieskończony oznacza, że zawsze można dodać kolejny człon i nie ma ostatniego członu szeregu.

P: Skąd wzięła się nazwa tego szeregu?

O: Nazwa tego szeregu pochodzi od pojęcia harmonii w muzyce, gdzie długość fali podtekstów wynosi 1/2, 1/3, 1/4, itd. długości fali fundamentalnej struny.

P: Co to jest średnia harmoniczna?

O: Średnia harmoniczna jest wtedy, gdy każdy termin w ciągu jest równy średniej harmonicznej sąsiednich terminów. To wyrażenie również pochodzi z muzyki.

P: Jak obliczamy każdy termin w tym ciągu?

O: Każdy wyraz tego ciągu można obliczyć, dzieląc jeden przez jego pozycję w ciągu (1/n).