Prędkość światła w próżni — definicja, wartość 299 792 458 m/s i znaczenie
Prędkość światła w próżni: definicja i dokładna wartość 299 792 458 m/s, znaczenie w teorii względności, E=mc², falach grawitacyjnych i przekazywaniu informacji.
Prędkość światła w pustej przestrzeni jest uniwersalną stałą fizyczną. Fizycy oznaczają ją literą c. Zgodnie z obowiązującą definicją jej wartość jest dokładnie 299 792 458 metrów na sekundę (czyli 983 571 056 stóp na sekundę). Foton (cząstka światła) porusza się z tą prędkością w próżni.
Definicja i pomiar
Od 1983 roku jednostka długości — metr — jest zdefiniowana poprzez prędkość światła: metr to droga przebyta przez światło w próżni w czasie 1/299 792 458 sekundy. W praktyce oznacza to, że c nie jest jedynie mierzonym parametrem, lecz wartością przyjętą definicyjnie, dzięki czemu jest ona dokładnie znana. Historycznie prędkość światła była określana pomiarami czasu przelotu, interferometrii oraz metodami opartymi na rezonansach fal elektromagnetycznych; współczesne ograniczenia różnic między obserwacjami a teorią dodatkowo potwierdzają jej stałość.
Rola w teorii względności i fizyce
Zgodnie ze szczególną względnością, c jest maksymalną prędkością, z jaką może przemieszczać się energia, materia i informacja. Jest to prędkość wszystkich bezmasowych cząstek oraz związanych z nimi pól, w tym promieniowania elektromagnetycznego jak światło w próżni. W teorii względności c łączy w sobie przestrzeń i czas i pojawia się w podstawowych związkach fizycznych, na przykład w równaniu równoważności masa–energia: E = mc2.
Szczególna teoria względności opiera się na dwóch podstawowych założeniach. Jednym z nich, potwierdzonym obserwacjami, jest to, że zmierzona prędkość światła w próżni jest taka sama niezależnie od wzajemnego ruchu źródła i obserwatora — często wyrażane jako "prędkość światła jest niezależna od ramy odniesienia". Drugim jest zasada względności (prawa fizyki są takie same we wszystkich inercjalnych układach odniesienia). W efekcie konsekwencją stałej wartości c są zjawiska takie jak dylatacja czasu, skrócenie długości i zależność masy efektywnej od prędkości.
Grawitacja i fale grawitacyjne
W ramach ogólnej teorii względności prędkość oddziaływania grawitacyjnego (fal grawitacyjnych) również wynosi, według obecnej teorii, c. Obserwacje astronomiczne, w tym jednoczesne wykrycie fal grawitacyjnych i promieniowania elektromagnetycznego z tego samego zdarzenia (np. zderzenie gwiazd neutronowych), dostarczyły silnych ograniczeń na różnicę prędkości grawitacji i światła, potwierdzając zgodność z c.
Światło w ośrodkach materialnych i pojęcie prędkości fazowej i grupowej
W ośrodkach materialnych światło porusza się wolniej niż w próżni: jego prędkość zależy od współczynnika załamania n, v = c/n. To spowolnienie wynika z oddziaływań pola elektromagnetycznego z materią. Istnieje także rozróżnienie między prędkością fazową, prędkością grupową i prędkością informacji — prędkość fazowa może lokalnie przekraczać c, a nawet być ujemna w niektórych układach, lecz nie prowadzi to do przesyłu informacji szybciej niż c. Informacja i sygnały nie mogą być przekazywane z prędkością większą niż c, co zapewnia zachowanie przyczynowości.
Konsekwencje i znaczenie praktyczne
- Metrologia: dzięki stałej wartości c możliwe jest precyzyjne definiowanie jednostek długości i czasu.
- Telekomunikacja i nawigacja: opóźnienia wynikające z ograniczenia prędkości sygnału są istotne przy projektowaniu systemów satelitarnych i sieci dalekosiężnych.
- Astronomia i kosmologia: prędkość światła wyznacza horyzonty obserwacyjne i pozwala mierzyć odległości kosmiczne (np. rok świetlny) oraz analizować sygnały od odległych źródeł.
- Fizyka fundamentalna: stałość c jest fundamentem teorii pola i relatywistycznej mechaniki kwantowej; każda wykryta zmiana tej wartości miałaby daleko idące konsekwencje.
Uwagi dodatkowe
Choć fotony mają zerową masę spoczynkową i poruszają się dokładnie z prędkością c, cząstki o niezerowej masie (np. elektrony, protony) zawsze poruszają się wolniej niż c. Drobne efekty, takie jak wpływ grawitacji na trajektorie światła (ugięcie promieniowania), nie zmieniają lokalnej wartości prędkości światła w próżni, lecz modyfikują geometrię przestrzeni i czasu, po których światło się porusza.
Podsumowując: prędkość światła w próżni c = 299 792 458 m/s jest jedną z najważniejszych stałych natury — kluczową dla zrozumienia struktury przestrzeni i czasu, dokładnej metrologii oraz wielu dziedzin współczesnej fizyki.
Przykład
Zachowanie to różni się od naszych wspólnych wyobrażeń na temat ruchu, jak pokazano na tym przykładzie:
George stoi na ziemi obok niektórych torów kolejowych (kolejowych). Pociąg pędzi z prędkością 48 km/h (30 mph). George rzuca piłkę baseballową z prędkością 90 mph (140 km/h) w kierunku, w którym porusza się pociąg. Tomek, pasażer pociągu, ma urządzenie (jak pistolet radarowy) do pomiaru prędkości rzutów. Ponieważ jest w pociągu, Tomek już jedzie z prędkością 30 mph (48 km/h) w kierunku rzutu, więc Tomek mierzy prędkość piłki tylko jako 60 mph (97 km/h).
Innymi słowy, prędkość baseballa, mierzona przez Toma w pociągu, zależy od prędkości pociągu.
W powyższym przykładzie pociąg poruszał się z prędkością 1/3 prędkości piłki, a prędkość piłki mierzona na pociągu wynosiła 2/3 prędkości rzutu mierzonej na podłoże.
Teraz powtórzyć eksperyment ze światłem zamiast z baseballem; to znaczy, że George ma latarkę zamiast rzucać baseballem. George i Tom mają takie same urządzenia do pomiaru prędkości światła (zamiast radaru w przykładzie baseballa).
George stoi na ziemi obok niektórych torów kolejowych. Jest tam pociąg pędzący z prędkością 1/3 prędkości światła. George miga promieniem światła w kierunku, w którym porusza się pociąg. George mierzy prędkość światła na 186,282 mil na sekundę (299,792 kilometrów na sekundę). Tomek, pasażer pociągu, mierzy prędkość wiązki światła. Jaką prędkość mierzy Tomek?
Intuicyjnie można pomyśleć, że prędkość światła z latarki mierzona w pociągu powinna wynosić 2/3 prędkości mierzonej na ziemi, podobnie jak prędkość baseballa 2/3. Ale w rzeczywistości, prędkość mierzona w pociągu jest pełną wartością, 186.282 mil na sekundę (299.792 kilometrów na sekundę), a nie 124.188 mil na sekundę (199.861 kilometrów na sekundę).
Brzmi to niemożliwie, ale to jest to, co się mierzy. Po części dlatego, że światło jest energią, która działa i porusza się w sposób bardzo różny od materii lub obiektów stałych, takich jak baseball.
Równania Maxwella przewidywały prędkość światła i potwierdziły ideę Michaela Faradaya, że światło to fala elektromagnetyczna (sposób przemieszczania się energii). Z równań tych wynika, że prędkość światła jest związana z odwrotnością pierwiastka kwadratowego dopuszczalności wolnej przestrzeni, ε0, oraz przepuszczalności wolnej przestrzeni, μ0:
c = 1 ε 0 μ 0 . {\i1}Displaystyle c{\i1}frac {\i1}sqrt {\i1}varepsilon _{0}mu _0}}}}\i0} . }
Konsekwencją tego faktu jest to, że nic nie może jechać szybciej niż prędkość światła. Kolejną konsekwencją jest to, że dla obiektów, które mają masę, bez względu na to, ile energii zużywa się do zwiększenia prędkości obiektu, będzie on coraz bliżej, ale nigdy nie osiągnie prędkości światła. Idee te zostały odkryte na początku XIX wieku przez Alberta Einsteina, którego praca całkowicie zmieniła nasze rozumienie światła.
Współczynnik załamania światła przezroczystego materiału jest to stosunek prędkości światła w próżni do prędkości światła w tym materiale.
Pomiar
Rømer
Ole Christensen Rømer zastosował pomiar astronomiczny, aby dokonać pierwszej ilościowej oceny prędkości światła. Przy pomiarze z Ziemi, okresy księżyców krążących wokół odległej planety są krótsze, gdy Ziemia zbliża się do planety, niż gdy Ziemia się od niej cofa. Odległość światła od planety (lub jej księżyca) do Ziemi jest krótsza, gdy Ziemia znajduje się w punkcie swojej orbity najbliższym swojej planecie, niż gdy Ziemia znajduje się w najdalszym punkcie swojej orbity, przy czym różnica w odległości jest równa średnicy orbity Ziemi wokół Słońca. Obserwowana zmiana w okresie orbitalnym Księżyca jest w rzeczywistości różnicą w czasie potrzebnym do pokonania krótszej lub dłuższej odległości. Rømer zaobserwował ten efekt dla najbardziej wewnętrznego Księżyca Io Jowisza i wydedukował, że światło potrzebuje 22 minut na przekroczenie średnicy orbity Ziemi.
Bradley
Inną metodą jest wykorzystanie aberracji światła, odkrytej i wyjaśnionej przez Jamesa Bradleya w XVIII wieku. Efekt ten wynika z dodania wektora prędkości światła docierającego z odległego źródła (takiego jak gwiazda) oraz prędkości jego obserwatora (patrz diagram po prawej stronie). Ruchomy obserwator widzi więc światło przychodzące z nieco innego kierunku i w konsekwencji widzi źródło w pozycji przesuniętej w stosunku do pozycji wyjściowej. Ponieważ kierunek prędkości Ziemi zmienia się nieustannie w miarę jak Ziemia krąży wokół Słońca, efekt ten powoduje pozorne przesunięcie pozycji gwiazd. Z różnicy kątowej w położeniu gwiazd można wyrazić prędkość światła w kategoriach prędkości Ziemi wokół Słońca. Prędkość tę, o znanej długości roku, można łatwo przeliczyć na czas potrzebny do podróży od Słońca do Ziemi. W 1729 r. Bradley użył tej metody, aby określić, że światło podróżowało 10.210 razy szybciej niż Ziemia na swojej orbicie (współczesna liczba wynosi 10.066 razy szybciej) lub, odpowiednio, że podróż ze Słońca na Ziemię zajęłaby 8 minut 12 sekund.
Nowoczesny
Obecnie "czas świetlny na jednostkę odległości" - odwrotność c (1/c), wyrażona w sekundach na jednostkę astronomiczną - jest mierzony poprzez porównanie czasu, w którym sygnały radiowe docierają do różnych statków kosmicznych w Układzie Słonecznym. Pozycja statku kosmicznego jest obliczana na podstawie efektów grawitacyjnych Słońca i różnych planet. Łącząc wiele takich pomiarów, uzyskuje się najlepszą wartość dla czasu świetlnego na jednostkę odległości. Według stanu na rok 2009[aktualizacja], najlepszym szacunkiem, zatwierdzonym przez Międzynarodową Unię Astronomiczną (IAU), jest:
czas oświetlenia dla odległości jednostki: 499.004783836(10) s
c = 0,00200398880410(4) AU/s
c = 173,144632674(3) AU/dzień.
Względna niepewność w tych pomiarach wynosi 0,02 części na miliard (2×10-11), co odpowiada niepewności w pomiarach długości Ziemi metodą interferometryczną. Ponieważ metr jest zdefiniowany jako długość pokonana przez światło w określonym przedziale czasu, pomiar czasu świetlnego dla jednostki odległości może być również interpretowany jako pomiar długości AU w metrach. Metr jest uważany za jednostkę odpowiedniej długości, podczas gdy AU jest często używany jako jednostka długości obserwowanej w danym zakresie odniesienia.
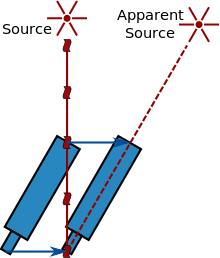
Aberracja światła: światło z odległego źródła wydaje się pochodzić z innego miejsca niż teleskop ruchomy ze względu na skończoną prędkość światła.
Praktyczne efekty
Skończona prędkość światła jest głównym ograniczeniem dla podróży kosmicznych na duże odległości. Zakładając podróż na drugą stronę Drogi Mlecznej, całkowity czas na przesłanie i jego odpowiedź wynosiłby około 200.000 lat. Co jeszcze poważniejsze, żaden statek kosmiczny nie mógłby podróżować szybciej niż światło, więc cały transport na skalę galaktyczną byłby skutecznie jednokierunkowy i trwałby znacznie dłużej niż jakakolwiek współczesna cywilizacja.
Prędkość światła może być również niepokojąca na bardzo krótkich dystansach. W superkomputerach prędkość światła narzuca ograniczenie na szybkość przesyłania danych pomiędzy procesorami. Jeśli procesor pracuje z prędkością 1 gigaherców, sygnał może przebyć maksymalnie około 30 centymetrów (1 ft) w jednym cyklu. Dlatego procesory muszą być umieszczone blisko siebie, aby zminimalizować opóźnienia w komunikacji; może to powodować trudności z chłodzeniem. Jeśli częstotliwości taktowania będą nadal rosły, prędkość światła stanie się w końcu czynnikiem ograniczającym wewnętrzną konstrukcję pojedynczych chipów.
Powiązane strony
Pytania i odpowiedzi
P: Jaka jest prędkość światła?
O: Prędkość światła, oznaczana jako "c", jest stałą fizyczną, która wynosi dokładnie 299 792 458 metrów na sekundę (983 571 056 stóp na sekundę).
P: Jak przedstawia się prędkość światła?
O: Prędkość światła jest zwykle oznaczana przez "c", a w ośrodku próżniowym jest oznaczana jako "c^0".
P: Jakie cząstki poruszają się z prędkością światła?
O: Fotony (cząstki światła) poruszają się z taką prędkością w próżni. Ponadto wszystkie bezmasowe cząstki, takie jak fotony i związane z nimi pola - w tym promieniowanie elektromagnetyczne, takie jak światło - poruszają się z prędkością c, niezależnie od ich źródła lub inercyjnego układu odniesienia obserwatora.
P: Co szczególna względność mówi o prędkości światła?
O: Według szczególnej teorii względności, c jest maksymalną prędkością, z jaką cała energia, materia i informacja fizyczna mogą poruszać się we wszechświecie. Stwierdza się również, że zmierzona prędkość światła w próżni pozostanie niezmieniona, niezależnie od tego, czy jego źródło lub obserwator poruszają się względem siebie.
P: Jak c łączy przestrzeń i czas?
O: W teorii względności c łączy przestrzeń i czas, pojawiając się w słynnym równaniu Einsteina E = mc2. To równanie pokazuje, jak energia może być przekształcana w masę i odwrotnie.
P: Czy istnieją jakieś dowody potwierdzające przewidywania szczególnej teorii względności dotyczące zmierzonej prędkości światła?
O: Tak - dotychczasowe obserwacje potwierdzają to przewidywanie, że niezależnie od tego, z jakiego układu odniesienia jest obserwowane i z jaką prędkością porusza się jego źródło - zmierzona prędkość pozostaje stała.
Przeszukaj encyklopedię
