Funkcja gęstości prawdopodobieństwa
Funkcja gęstości prawdopodobieństwa jest funkcją, która może być zdefiniowana dla każdego ciągłego rozkładu prawdopodobieństwa. Całość funkcji gęstości prawdopodobieństwa w przedziale czasu [ a , b ] {\i1} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
daje prawdopodobieństwo, że dana zmienna losowa o danej gęstości jest zawarta w podanym przedziale czasu.
Funkcja gęstości prawdopodobieństwa jest konieczna, aby móc pracować z rozkładami ciągłymi. Rzucanie kostką daje liczby od 1 do 6, z prawdopodobieństwem 1 6. 
ale nie jest to funkcja ciągła, ponieważ możliwe są tylko cyfry od 1 do 6. W przeciwieństwie do tego, dwie osoby nie będą miały tego samego wzrostu, ani tej samej wagi. Używając funkcji gęstości prawdopodobieństwa, można określić prawdopodobieństwo dla osób pomiędzy 180 cm (71 cali) a 181 cm (71 cali) lub pomiędzy 80 kilogramami (176,4 lb) a 81 kilogramami (178,6 lb), mimo że pomiędzy tymi dwoma granicami jest nieskończenie wiele wartości.
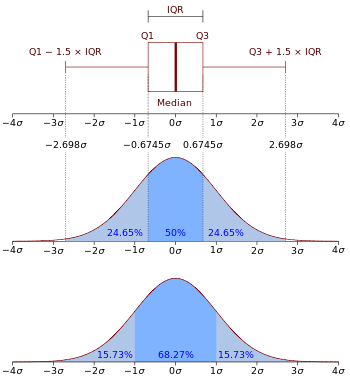
Boxplot i funkcja gęstości prawdopodobieństwa rozkładu normalnego N(0,∙σ2) .
Pytania i odpowiedzi
P: Co to jest funkcja gęstości prawdopodobieństwa?
A: Funkcja gęstości prawdopodobieństwa to funkcja charakteryzująca dowolny ciągły rozkład prawdopodobieństwa.
P: Jak zapisuje się funkcję gęstości prawdopodobieństwa zmiennej losowej X?
O: Funkcję gęstości prawdopodobieństwa X zapisuje się czasami jako f_X(x).
P: Co oznacza całka z funkcji gęstości prawdopodobieństwa?
O: Całka z funkcji gęstości prawdopodobieństwa przedstawia prawdopodobieństwo, że dana zmienna losowa o danej gęstości znajduje się w podanym przedziale.
P: Czy funkcja gęstości prawdopodobieństwa jest zawsze nieujemna w całej swojej dziedzinie?
O: Tak, z definicji funkcja gęstości prawdopodobieństwa jest nieujemna w całej swojej dziedzinie.
P: Czy całkowanie po przedziale sumuje się do 1?
O: Tak, całkowanie po przedziale sumuje się do 1.
P: Jaki rodzaj rozkładu charakteryzuje funkcja gęstości prawdopodobieństwa?
O: Funkcja gęstości prawdopodobieństwa charakteryzuje każdy ciągły rozkład prawdopodobieństwa.
