Iloczyn skalarny

Definicja

Iloczyn punktowy dwóch wektorów a = [a1, a2, ..., _an] i b = [b1, b2, ..., bn] definiuje się jako:

 

gdzie Σ oznacza notację sumacyjną (suma wszystkich członów), a n jest wymiarem przestrzeni wektorowej.

W wymiarze 2, iloczyn punktowy wektorów [a,b] i [c,d] wynosi ac + bd. Analogicznie, w wymiarze 3 iloczyn punktowy wektorów [a,b,c] i [d,e,f] wynosi ad + be + cf. Na przykład, iloczyn punktowy dwóch trójwymiarowych wektorów [1, 3, -5] i [4, -2, -1] wynosi

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( - 5 ) × ( - 1 ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. { {displaystyle [1,3,-5]∗ [4,-2,-1]=(1 razy 4)+(3 razy (-2))+((-5)∗ (-1))=(4)-(6)+(5)=3.}

Interpretacja geometryczna

W geometrii euklidesowej iloczyn punktowy, długość i kąt są ze sobą powiązane. Dla wektora a, iloczyn kropkowy a - a jest kwadratem długości a, lub

a ⋅ a = ‖ a ‖ 2 {{displaystyle {{mathbf {{a}} \\{cdot \mathbf {{a}} }= lewa strona \mathbf {a} \prawa ^{2}}

gdzie |a|| oznacza długość (wielkość) a. Ogólniej, jeśli b jest innym wektorem

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {displaystyle \mathbf {a} \cdot \mathbf {b} = \left \mathbf {a} \prawo \,\left \mathbf {b}

gdzie |a|| i |b|| oznaczają długości a i b, a θ jest kątem między nimi.

Wzór ten można przekształcić, aby wyznaczyć wielkość kąta między dwoma niezerowymi wektorami:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {{displaystyle \theta = arccos \left({{frac {{mathbf {a}}cdot {{mathbf {b}}}}{{mathbf {a}}}right|{mathbf {b}}}right}}}}.

Można też najpierw przekształcić wektory na wektory jednostkowe, dzieląc je przez ich wielkość:

a ^ = a ‖ a ‖ {displaystyle {{{boldsymbol {{hat {a}}}}={frac {{mathbf {a}}}{{left}}|{mathbf {a}}}right}}}.

wtedy kąt θ jest dany przez

θ = arccos ( a ^ ⋅ b ^ ) { θ = arccos(a ^ ⋅ b ^}} { θ = arccos(a ^ ⋅ ⋅ b ^}}}

Ponieważ cosinus kąta 90° wynosi zero, iloczyn punktowy dwóch ortogonalnych (prostopadłych) wektorów jest zawsze równy zero. Co więcej, dwa wektory można uznać za ortogonalne wtedy i tylko wtedy, gdy ich iloczyn punktowy jest równy zero, a oba mają niezerową długość. Własność ta dostarcza prostej metody do testowania warunku ortogonalności.

Czasami własności te wykorzystuje się również do definiowania iloczynu punktowego, zwłaszcza w 2 i 3 wymiarach; definicja ta jest równoważna powyższej. Dla wyższych wymiarów wzór ten może być użyty do zdefiniowania pojęcia kąta.

Własności geometryczne polegają na tym, że podstawa jest ortonormalna, tzn. składa się z parami prostopadłych wektorów o jednostkowej długości.

Rzutowanie skalarne

Jeśli a i b mają długość jeden (tzn. są wektorami jednostkowymi), to ich iloczyn punktowy daje po prostu cosinus kąta między nimi.

Jeśli tylko b jest wektorem jednostkowym, to iloczyn kropkowy a - b daje |a| cos(θ), czyli wielkość rzutu a w kierunku b, ze znakiem minus, jeśli kierunek jest przeciwny. Nazywamy to rzutem skalarnym a na b lub składową skalarną a w kierunku b (patrz rysunek). Ta własność iloczynu punktowego ma kilka użytecznych zastosowań (na przykład, zobacz następny rozdział).

Jeśli ani a, ani b nie są wektorami jednostkowymi, to na przykład wielkość rzutu a w kierunku b będzie wynosić a - (b / |b|), ponieważ wektorem jednostkowym w kierunku b jest b / |b|.

Obrót

Rotację bazy ortonormalnej, w której reprezentowany jest wektor a, uzyskuje się poprzez pomnożenie a przez macierz rotacji R. To mnożenie macierzowe jest po prostu zwartą reprezentacją ciągu iloczynów kropkowych.

Na przykład, niech

• _B1 = {x, y, z} oraz _B2 = {u, v, w} są dwiema różnymi bazami ortonormalnymi tej samej przestrzeni R3, przy czym _B2 otrzymujemy przez obrócenie _B1,
• a1 = (_ax, ay, _az) przedstawia wektor a w kategoriach _B1,
• a2 = (_au, _av, _aw) przedstawiają ten sam wektor w kategoriach obróconej podstawy _B2,
• u1, v1, w1 są obróconymi wektorami bazowymi u, v, w przedstawionymi w kategoriach _B1.

Następnie obrót z _B1 do _B2 jest wykonywany w następujący sposób:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}}}cdot {{mathbf {a}}_{1}} {w}}_{1}}}cdot {{mathbf {a}}_{1}}}}}={begin{bmatrix}a_{u}}}}}a_{v}}}}}}end{bmatrix}}. }

Zauważmy, że macierz rotacji R jest utworzona z obróconych wektorów bazowych u1, v1, w1 jako jej wierszy, a wektory te są wektorami jednostkowymi. Z definicji Ra1 składa się z ciągu iloczynów punktowych pomiędzy każdym z trzech rzędów R i wektorem a1. Każdy z tych iloczynów punktowych wyznacza składową skalarną a w kierunku obróconego wektora bazowego (patrz poprzedni rozdział).

Jeśli a1 jest wektorem wierszowym, a nie kolumnowym, to R musi zawierać obrócone wektory bazowe w swoich kolumnach i musi pomnożyć a1:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {{displaystyle}}={mathbf {a}}_{2}={mathbf {a}}_{1}}{{mathbf {R}}}={begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}}}={begin{bmatrix}{bmathbf {u}}_{1}} {cdot {mathbf {a}}}&{mathbf {v}}_{1}} {cdot {mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

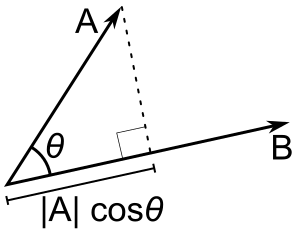
A - B = |A| |B| cos(θ). |A| cos(θ) jest rzutem skalarnym A na B.

Fizyka

W fizyce wielkość jest skalarem w sensie fizycznym, tzn. wielkością fizyczną niezależną od układu współrzędnych, wyrażoną jako iloczyn wartości liczbowej i jednostki fizycznej, a nie tylko liczby. Iloczyn punktowy jest również skalarem w tym sensie, danym wzorem, niezależnym od układu współrzędnych. Przykład:

• Praca mechaniczna to iloczyn punktowy wektorów siły i przemieszczenia.
• Strumień magnetyczny jest iloczynem punktowym pola magnetycznego i wektorów powierzchni.
• Objętościowe natężenie przepływu jest iloczynem punktowym wektorów prędkości płynu i powierzchni.

Właściwości

Następujące własności zachodzą, jeśli a, b i c są wektorami rzeczywistymi, a r jest skalarem.

Iloczyn kropkowy jest komutatywny:

a ⋅ b = b ⋅ a . {\i1}displaystyle \mathbf {a} \i0} = \i0}mathbf {b} = \mathbf {a} . }

Iloczyn kropkowy jest dystrybuantą względem dodawania wektorów:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\a} \mathbf {a} \cdot (\mathbf {b} + \mathbf {c} )= \mathbf {a} \a} \mathbf {b} + \mathbf {a} \cdot \mathbf {c} . }

Iloczyn punktowy jest bilinearny:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) .  }

W przypadku mnożenia przez wartość skalarną, iloczyn kropkowy spełnia warunki:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {cdot (c_{1} ⋅ (c_{2} ⋅ (c_{1} ⋅ (c_{2} ⋅ (c_{1}c_{2})(c 1 c 2 ) ( a ⋅ b )} }

(te dwie ostatnie własności wynikają z dwóch pierwszych).

Dwa niezerowe wektory a i b są prostopadłe wtedy i tylko wtedy, gdy a - b = 0.

W przeciwieństwie do mnożenia zwykłych liczb, gdzie jeśli ab = ac, to b zawsze równa się c, chyba że a jest równe zero, iloczyn kropkowy nie przestrzega prawa anulowania:

Jeśli a - b = a - c oraz a ≠ 0, to możemy napisać: a - (b - c) = 0 na mocy prawa rozdzielności; powyższy wynik mówi, że oznacza to tylko, że a jest prostopadłe do (b - c), co nadal pozwala na to, że (b - c) ≠ 0, a zatem b ≠ c.

Zakładając, że podstawa jest ortonormalna, iloczyn punktowy jest niezmienny przy izometrycznych zmianach podstawy: obrotach, odbiciach i kombinacjach, przy zachowaniu stałego początku. Na tej własności opiera się wspomniana wyżej interpretacja geometryczna. Innymi słowy, dla przestrzeni ortonormalnej o dowolnej liczbie wymiarów iloczyn punktowy jest niezmienniczy przy przekształceniach współrzędnych opartych na macierzy ortogonalnej. Odpowiadają temu dwa następujące warunki:

• Nowa baza jest ponownie ortonormalna (tzn. jest ortonormalna wyrażona w starej bazie).
• Nowe wektory bazowe mają taką samą długość jak stare (tzn. długość jednostkową w odniesieniu do starej bazy).

Jeżeli a i b są funkcjami, to pochodna a - b jest równa a' - b + a - b'

Potrójne rozszerzenie iloczynu

Jest to bardzo przydatna tożsamość (znana również jako wzór Lagrange'a) dotycząca iloczynów kropkowych i krzyżowych. Zapisuje się ją jako

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) { {displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )= \mathbf {b} (\mathbf {a} \cdot \mathbf {c} )- \mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

co jest łatwiejsze do zapamiętania jako "BAC minus CAB", pamiętając, które wektory są razem kropkowane. Wzór ten jest powszechnie używany do uproszczenia obliczeń wektorowych w fizyce.

Dowód interpretacji geometrycznej

Rozważmy element Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . =v_{1} =v_{1} =v_{2} =v_{2} =v_{2} =v_{2} =v_{1} =v_{2} =v_{2} =v_{2} _{1}+v_{2} {mathbf {e}} _{2}+...+v_{n}}mathbf {{hat {e}} _{n}.\,}

Wielokrotne zastosowanie twierdzenia Pitagorejskiego daje dla jego długości |v|

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\i1}displaystyle {\i1}mathbf {\i0} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Ale to jest to samo, co

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , { {{displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},}

Stąd wniosek, że iloczyn punktowy wektora v z samym sobą daje długość wektora podniesioną do kwadratu.

Lemat 1

v ⋅ v = | v | 2 . {\i1}displaystyle \i1}mathbf {\i1} \i1}mathbf {\i1} =|mathbf {\i1}. |^{2}.\,}

Rozważmy teraz dwa wektory a i b wychodzące z początku, oddzielone od siebie kątem θ. Trzeci wektor c można zdefiniować jako

c = d e f a - b . {displaystyle {mathbf {c} {stackrel {mathrm {def} {{=}} \u200} - \u200} - \u200} \u200} \u200}

tworząc trójkąt o bokach a, b i c. Zgodnie z prawem cosinusów mamy

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ . W związku z tym, że nie jest to możliwe |{2}=|mathbf {a} |^{2}+|mathbf {b} |^{2}-2|mathbf {a} ||mathbf {b} |}.

Podstawiając iloczyny punktowe do kwadratów długości zgodnie z Lemmą 1, otrzymujemy

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\i1}displaystyle \i0} = \mathbf {c} = \mathbf {a} \dot \mathbf {a} + \mathbf {b} \cdot \mathbf {b} -2|mathbf {a} ||mathbf {b} |cos \theta \, } (1)

Ale ponieważ c ≡ a - b, mamy również

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\an8}

która zgodnie z prawem rozdzielczym rozszerza się do

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\i1}displaystyle \i0} = \i0}mathbf {\i0} \cdot \mathbf {c} = \mathbf {a} \cdot \mathbf {a} + \mathbf {b} =mathbf {a} +mathbf {b} -2(\mathbf {a} \mathbf {b} ).} (2)

Łącząc dwa równania c - c, (1) i (2), otrzymujemy

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ .  = \mathbf {a} \mathbf {b} -2(\mathbf {a} \mathbf {b} )= \mathbf {a} \mathbf {a} + \mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||mathbf {b} |cos \theta \, }

Odejmując a - a + b - b od obu stron i dzieląc przez -2 otrzymujemy

a ⋅ b = | a | | b | cos θ . {\i1}displaystyle \i0} \i0} \i0} =|\i0}mathbf {\i0} =|mathbf {a} ||mathbf {b} =|mathbf {a} ||mathbf {b} ||cos ™theta

Q.E.D.

Generalizacja

 \rangle } . Ze względu na geometryczną interpretację iloczynu punktowego norma ||a|| wektora a w takiej przestrzeni iloczynu wewnętrznego jest zdefiniowana jako

‖ a ‖ = ⟨ a , a ⟩ {{displaystyle \|mathbf {a} \}={sqrt {{langle \mathbf {a} \,,\mathbf {a} \rangle }}

tak, że uogólnia długość, a kąt θ między dwoma wektorami a i b przez

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . ‖ ‖ ‖ ‖ ‖ ‖ ‖ b‖ . {frac {{frac {{mathbf {a} \, ,\{mathbf {b} \|}}. }

W szczególności, dwa wektory są uważane za ortogonalne, jeśli ich iloczyn wewnętrzny wynosi zero

⟨ a , b ⟩ = 0. {displaystyle ⟨ a , b ⟩ = 0. ⟩ =0.}

Dla wektorów o złożonych wejściach, użycie podanej definicji iloczynu kropkowego prowadziłoby do całkiem innych własności geometrycznych. Na przykład iloczyn punktowy wektora z samym sobą może być dowolną liczbą złożoną i może wynosić zero, przy czym wektor nie jest wektorem zerowym; to z kolei miałoby poważne konsekwencje dla takich pojęć jak długość i kąt. Wiele własności geometrycznych można uratować, kosztem rezygnacji z symetrycznych i biliniowych własności iloczynu skalarnego, definiując alternatywnie

a ⋅ b = ∑ a i b i ¯ {displaystyle \mathbf {a} \cdot \mathbf {b} = \suma {a_{i}{\overline {b_{i}}}}}

gdzie _bi jest koniugatem zespolonym _bi. Wtedy iloczyn skalarny dowolnego wektora z samym sobą jest nieujemną liczbą rzeczywistą i jest niezerowy z wyjątkiem wektora zerowego. Jednak ten iloczyn skalarny nie jest liniowy w b (ale raczej sprzężony liniowy), a iloczyn skalarny nie jest też symetryczny, ponieważ

a ⋅ b = b ⋅ a {{displaystyle \mathbf {a} \cdot \mathbf {b} ={overline \mathbf {b} } }}} .

Ten typ iloczynu skalarnego jest jednak dość użyteczny i prowadzi do pojęć formy hermitowskiej oraz ogólnych przestrzeni iloczynów wewnętrznych.

Wewnętrzny iloczyn Frobeniusa jest uogólnieniem iloczynu kropkowego na macierze. Jest on zdefiniowany jako suma iloczynów odpowiednich składników dwóch macierzy o tym samym rozmiarze.

Uogólnienie na tensory

Iloczyn kropkowy pomiędzy tensorem rzędu n i tensorem rzędu m jest tensorem rzędu n+m-2. Iloczyn punktowy uzyskuje się przez mnożenie i sumowanie przez jeden indeks w obu tensorach. Jeżeli A {displaystyle \mathbf {A} } i B {displaystyle \mathbf {B} } są dwoma tensorami z reprezentacją elementów A i j ... k ℓ ... {displaystyle A_{ij}}^{k}} i B m n ... p ... i {displaystyle B_{mn}}^{p}} elementy iloczynu punktowego A ⋅ B {displaystyle \mathbf {A}} ^{mathbf {B} } są dane przez

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {{displaystyle A_{ij}dots B_{mn\dots }^{p{dots }i}=suma _{i=1}^{n}A_{ij\dots }^{k{ell \dots } B_{mn\dots }^{p{dots }i}

Definicja ta w naturalny sposób redukuje się do standardowego iloczynu wektorowego, gdy jest stosowany do wektorów, i mnożenia macierzowego, gdy jest stosowany do macierzy.

Czasami podwójny iloczyn kropkowy jest używany do reprezentowania mnożenia i sumowania przez dwa indeksy. Podwójny iloczyn kropkowy pomiędzy dwoma tensorami drugiego rzędu jest skalarem.

Powiązane strony

• Nierówność Cauchy'ego-Schwarza
• Produkt krzyżowy
• Mnożenie macierzowe
• Fizyka