Moment magnetyczny (dipolowy): definicja, wzory i zastosowania
Dowiedz się, czym jest moment magnetyczny (dipolowy): definicja, wzory, intuicyjne objaśnienia i praktyczne zastosowania w magnetyzmie, elektronice i fizyce.
Moment magnetyczny magnesu jest wielkością, która określa siłę, jaką magnes może wywierać na prąd elektryczny oraz moment obrotowy, jaki wywiera na niego pole magnetyczne. Pętla prądu elektrycznego, magnes sztabkowy, elektron, cząsteczka i planeta — wszystkie te obiekty mają momenty magnetyczne. Moment magnetyczny określa więc zdolność obiektu do oddziaływania z zewnętrznym polem magnetycznym oraz do wytwarzania własnego pola magnetycznego.
Zarówno moment magnetyczny jak i pole magnetyczne mogą być traktowane jako wektory posiadające wielkość i kierunek. Kierunek momentu magnetycznego jest skierowany od południowego do północnego bieguna magnesu. Pole magnetyczne wytwarzane przez magnes jest również proporcjonalne do jego momentu magnetycznego. Dokładniej, termin moment magnetyczny zwykle odnosi się do magnetycznego momentu dipolowego układu, który tworzy pierwszy człon w multipolowym rozwinięciu ogólnego pola magnetycznego. Składowa dipolowa pola magnetycznego obiektu jest symetryczna względem kierunku jego magnetycznego momentu dipolowego i maleje jako odwrotność sześcianu odległości od obiektu.
Definicja i podstawowe wzory
Dla prostego przewodzącego obwodu w kształcie pętli o powierzchni A, przez którą płynie prąd I, wektorowy moment magnetyczny m definiuje się jako:
- m = I · A (dla pojedynczej pętli, kierunek nadaje reguła prawej dłoni — palce zgodnie z prądem, kciuk wskazuje kierunek m). Dla cewki z N zwojami: m = N·I·A.
- Moment ten ma jednostkę układu SI: amper·metr kwadratowy (A·m2).
Oddziaływanie momentu magnetycznego z zewnętrznym polem B opisują najważniejsze zależności używane w praktyce:
- Moment siły (moment obrotowy) działający na dipol: τ = m × B. Oznacza to, że dipol dąży do obrócenia się tak, aby m ustawić równolegle do pola B.
- Energia potencjalna dipola w polu: U = − m · B. Dipol ma najmniejszą energię, gdy jego moment jest ustawiony równolegle do pola.
Pole magnetyczne dipola (pola dalekiego pola)
Pole magnetyczne daleko od punktowego dipola magnetycznego opisywane jest wzorem (w przybliżeniu dalekiego pola), który pokazuje zależność 1/r3 i kierunkową anizotropię pola. W układzie SI:
B(r) = (μ0/4π) · [ (3 r̂ (m · r̂) − m) / r3 ],
gdzie μ0 ≈ 4π·10−7 N/A2 jest przenikalnością magnetyczną próżni, r — wektor od dipola do punktu obserwacji, a r̂ = r / |r|.
To wyjaśnia, dlaczego pole dipola szybko maleje z odległości i ma charakterystyczny układ linii pola (wychodzących z bieguna północnego i powracających do południowego na zewnątrz dipola).
Moment magnetyczny w skali atomowej i elementarnej
W atomach i cząsteczkach moment magnetyczny pochodzi z ruchu orbitalnego elektronów oraz z ich spinu. Typową jednostką dla momentu magnetycznego elektronów jest magneton Bohra:
μB = e ħ / (2 me) ≈ 9,274 × 10−24 A·m2.
Dla elektronu całkowity moment magnetyczny związany ze spinem można zapisać w postaci m = −g (e/2me) S, gdzie g to czynnik Landé, a S — moment pędu spinowego.
Powiązania z magnetyzacją i wielkościami makroskopowymi
W materiałach magnetycznych użyteczna jest wielkość zwana magnetyzacją M, czyli momentem magnetycznym na jednostkę objętości. Całkowity moment magnetyczny obiektu o objętości V to m = ∫V M dV. Dla ciał stałych moment magnetyczny może wynikać z uporządkowania momentów atomowych (np. w ferromagnetykach) lub z prądów makroskopowych (np. cewki).
Przykłady i zastosowania
- W silnikach elektrycznych i generatorach: moment magnetyczny prądu w polu magnetycznym daje moment obrotowy (zasada działania silników).
- W magnetycznym rezonansie jądrowym (MRI) i spektroskopii: jądra atomowe mają momenty magnetyczne, które oddziałują z zewnętrznym polem B i mogą być wykorzystane do obrazowania oraz analizy struktury materiałów.
- W kompaniach i kompasach: geomagnetyczny moment planety (np. Ziemi) określa orientację pola i jego wpływ na nawigację.
- W przechowywaniu danych magnetycznych: nośniki magnetyczne wykorzystują momenty drobnych domen magnetycznych do zapisu bitów.
- Pomiary momentów magnetycznych wykonywane są za pomocą magnetometrów i momentomierzy, a analiza multipolowa (gdzie dipol jest składową najważniejszą) używana jest w geofizyce i astrofizyce.
Podsumowanie
Moment magnetyczny to kluczowa wielkość opisująca zdolność obiektu do tworzenia pola magnetycznego i oddziaływania z zewnętrznym polem. Jego wektorowy charakter oraz proste zależności (m = I·A, τ = m × B, U = −m·B) pozwalają przewidzieć zachowanie dipoli magnetycznych w wielu układach od elementarnych cząstek po planety. Składowa dipolowa pola jest najważniejsza w opisie oddziaływań na duże odległości ze względu na swoje charakterystyczne zanikanie ∼1/r3.
Dwie definicje momentu
W podręcznikach do definiowania momentów magnetycznych stosowane są dwa uzupełniające się podejścia. W podręcznikach sprzed lat 30-tych definiowano je za pomocą biegunów magnetycznych. W większości najnowszych podręczników definiuje się je w kategoriach prądów Ampèriana.
Definicja bieguna magnetycznego
Fizycy przedstawiają źródła momentów magnetycznych w materiałach jako bieguny. Bieguny północny i południowy są analogią do ładunków dodatnich i ujemnych w elektrostatyce. Rozważmy magnes sztabkowy, który ma bieguny magnetyczne o równej wielkości, ale przeciwnej polaryzacji. Każdy z biegunów jest źródłem siły magnetycznej, która słabnie wraz z odległością. Ponieważ bieguny magnetyczne zawsze występują parami, ich siły częściowo się znoszą, ponieważ podczas gdy jeden biegun przyciąga, drugi odpycha. To zniesienie jest największe, gdy bieguny są blisko siebie, tzn. gdy magnes sztabkowy jest krótki. Siła magnetyczna wytwarzana przez magnes sztabkowy, w danym punkcie przestrzeni, zależy więc od dwóch czynników: zarówno od siły p {styl p}
jego biegunów, jak i od wektora l {styl lathbf {l} } 
oddzielającego je. Moment definiuje się jako
m = p l . {{displaystyle \mathbf {m} =p\mathbf {l} . } 
Skierowany jest w kierunku od bieguna południowego do północnego. Analogia z dipolami elektrycznymi nie powinna być zbyt daleko posunięta, ponieważ dipole magnetyczne są związane z momentem pędu (patrz: Moment magnetyczny i moment pędu). Niemniej jednak, bieguny magnetyczne są bardzo przydatne w obliczeniach magnetostatycznych, szczególnie w zastosowaniach do ferromagnetyków. Praktycy stosujący metodę biegunów magnetycznych na ogół przedstawiają pole magnetyczne jako pole irrotacyjne H { {displaystyle ™mathbf {H} } 
w analogii do pola elektrycznego E {displaystyle \mathbf {E} } 
.
Definicja pętli prądowej
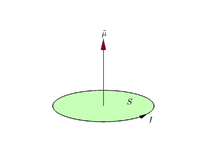
Załóżmy, że planarna pętla zamknięta przewodzi prąd elektryczny I 
i ma pole wektorowe S. } 
( x {displaystyle x} 
, y {displaystyle y} , i z {displaystyle z} ). 
i z {displaystyle z} 
współrzędne tego wektora są obszarami rzutów pętli na punkty y z {displaystyle yz}, z x {displaystyle yz} i z {displaystyle z}. 
, z x {displaystyle zx} 
i x y {displaystyle xy}
). Jej moment magnetyczny m {{displaystyle ™mathbf {m} } 
, wektor, jest zdefiniowany jako:
m = I S . { {displaystyle \mathbf {m} =Imathbf {S} . } 
Umownie kierunek obszaru wektorowego określa zasada chwytu prawą ręką (zawinięcie palców prawej ręki w kierunku prądu wokół pętli, gdy dłoń "dotyka" zewnętrznej krawędzi pętli, a wyprostowany kciuk wskazuje kierunek obszaru wektorowego, a więc i momentu magnetycznego).
Jeśli pętla nie jest planarna, moment jest określany jako
m = I 2 ∫ r × d r . ={frac {I}{2}}}int \mathbf {r} . \frac {I}{2}}int \mathbf {r} . } 
W najbardziej ogólnym przypadku dowolnego rozkładu prądu w przestrzeni, moment magnetyczny takiego rozkładu można znaleźć z następującego równania:
m = 1 2 ∫ r × J d V , {displaystyle \mathbf {m} = {frac {1}{2}}int \mathbf {r} {\i1}times \i0} {{frac {d}}V,} 
gdzie r {displaystyle \mathbf {r} } 
jest wektorem położenia skierowanym od początku do miejsca, w którym znajduje się element objętości, a J {displaystyle \mathbf {J} } 
jest wektorem gęstości prądu w tym miejscu.
Powyższe równanie można wykorzystać do obliczenia momentu magnetycznego dowolnego zespołu poruszających się ładunków, np. wirującego naładowanego ciała stałego, podstawiając
J = ρ v , { {displaystyle \mathbf {J} = \rho \mathbf {v} ,} 
gdzie ρ { 
jest gęstością ładunku elektrycznego w danym punkcie, a v { 
jest chwilową prędkością liniową tego punktu.
Na przykład, moment magnetyczny wytwarzany przez ładunek elektryczny poruszający się po torze kołowym wynosi
m = 1 2 q r × v { {displaystyle \mathbf {m} ={frac {1}{2}}}, q, \mathbf {r}. \times \mathbf {v} } 
,
gdzie r {displaystyle \mathbf {r} } jest położeniem ładunku q {displaystyle q} 
względem środka okręgu, a v {displaystyle \mathbf {v} } jest prędkością chwilową ładunku.
Praktycy stosujący model pętli prądowej zwykle przedstawiają pole magnetyczne jako pole solenoidalne B { {displaystyle ™mathbf {B} } 
, analogicznie do pola elektrostatycznego D {displaystyle \mathbf {D} } 
.
Moment magnetyczny solenoidu
Uogólnieniem powyższej pętli prądowej jest cewka wieloobrotowa, czyli solenoid. Jej moment jest sumą wektorową momentów poszczególnych zwojów. Jeżeli solenoid ma N 
{jednakowych zwojów (uzwojenie jednowarstwowe),
m = N I S . { {displaystyle \mathbf {m} =NI\mathbf {S} . } 
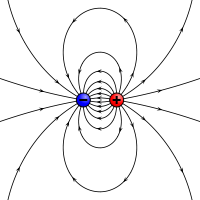
Elektrostatyczny odpowiednik momentu magnetycznego: dwa przeciwne ładunki oddzielone od siebie skończoną odległością.
Moment m {styl \mathbf {m} } planarnej pętli prądowej o powierzchni S {displaystyle S} 
i prądzie I {displaystyle I} .
Trójwymiarowy obraz solenoidu.
Jednostki
Jednostka momentu magnetycznego nie jest jednostką podstawową w Międzynarodowym Układzie Jednostek Miar (SI) i może być reprezentowana na więcej niż jeden sposób. Na przykład, w definicji pętli prądowej, powierzchnia jest mierzona w metrach kwadratowych, a I {tekstekst} jest mierzone w amperach, więc moment magnetyczny jest mierzony w amperach-metrach kwadratowych ( A m 2 {tekst}^{2}}
). W równaniu na moment obrotowy na moment, moment obrotowy jest mierzony w niutonometrach, a pole magnetyczne w teslach, więc moment jest mierzony w N.m na Teslę ( N.m T - 1 {displaystyle {text{N.m T}}^{-1}}
). Te dwie reprezentacje są równoważne:
A m 2 = N.m T - 1 . A m}^{2} = N.m T}^{-1}. } 
W systemie CGS istnieje kilka różnych zestawów jednostek elektromagnetyzmu, z których główne to ESU, Gaussian i EMU. Wśród nich są dwie alternatywne (nierównoważne) jednostki magnetycznego momentu dipolowego w CGS:
(ESU CGS) 1 statA-cm² = 3.33564095×10-14 (m2-A lub N.m/T)
oraz (częściej stosowane)
(EMU CGS i Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m2-A lub N.m/T).
Stosunek tych dwóch nierównoważnych jednostek CGS (EMU/ESU) jest równy dokładnie prędkości światła w wolnej przestrzeni, wyrażonej w cm/s.
Wszystkie wzory w tym artykule są poprawne w jednostkach SI, ale w innych układach jednostek wzory mogą wymagać zmiany. Na przykład, w jednostkach SI pętla prądu o natężeniu I i powierzchni A ma moment magnetyczny I×A (patrz poniżej), ale w jednostkach gaussowskich moment magnetyczny wynosi I×A/c.
| Wewnątrzcząsteczkowe momenty magnetyczne i spiny niektórych cząstek elementarnych | ||
| Cząstki stałe | Magnetyczny moment dipolowy w jednostkach SI (10-27 J/T) | Spinowa liczba kwantowa (bezwymiarowa) |
| -9284.764 | 1/2 | |
| proton | 14.106067 | 1/2 |
| neutron | -9.66236 | 1/2 |
| mion | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
Związek między pojęciami momentu magnetycznego i namagnesowania patrz namagnesowanie.
Pytania i odpowiedzi
P: Jaki jest moment magnetyczny magnesu?
O: Moment magnetyczny magnesu to wielkość, która określa siłę, jaką magnes może wywierać na prądy elektryczne oraz moment obrotowy, jaki wywiera na niego pole magnetyczne.
P: Które obiekty mają moment magnetyczny?
O: Pętla prądu elektrycznego, magnes sztabkowy, elektron, cząsteczka i planeta mają momenty magnetyczne.
P: W jaki sposób można rozpatrywać zarówno moment magnetyczny, jak i pole magnetyczne?
O: Zarówno moment magnetyczny jak i pole magnetyczne mogą być traktowane jako wektory posiadające wielkość i kierunek.
P: W którym kierunku skierowany jest moment magnetyczny magnesu?
O: Kierunek momentu magnetycznego wskazuje od południowego do północnego bieguna magnesu.
P: Jaki jest związek między momentem magnetycznym a polem magnetycznym magnesu?
O: Pole magnetyczne wytwarzane przez magnes jest proporcjonalne do jego momentu magnetycznego.
P: Do czego zwykle odnosi się termin moment magnetyczny?
O: Dokładniej, termin moment magnetyczny zwykle odnosi się do magnetycznego momentu dipolowego układu, który wytwarza pierwszy człon w rozwinięciu multipolowym ogólnego pola magnetycznego.
P: Jak zachowuje się składowa dipolowa pola magnetycznego obiektu wraz ze wzrostem odległości od obiektu?
O: Składowa dipolowa pola magnetycznego obiektu jest symetryczna względem kierunku jego magnetycznego momentu dipolowego i maleje jako odwrotność sześcianu odległości od obiektu.
Przeszukaj encyklopedię