Złoty podział
W przypadku jednej liczby a i drugiej, mniejszej liczby b, stosunek tych dwóch liczb ustala się przez podzielenie ich. Ich stosunek wynosi a/b. Inny stosunek można znaleźć dodając te dwie liczby razem a+b i dzieląc je przez większą liczbę a. Nowy stosunek wynosi (a+b)/a. Jeżeli te dwa współczynniki są równe tej samej liczbie, to ta liczba jest nazywana złotym stosunkiem. Grecka litera φ {\i1} {\i1}wyraźny styl \i0} 
(phi) jest zwykle używany jako nazwa dla złotego stosunku.
Na przykład, jeżeli b = 1 i a/b = φ {\i1}displaystylu \i0}varphi \i0} a następnie a = Displaystyle Varphi. . Druga proporcja (a+b)/a wynosi wtedy ( φ + 1 ) / φ {\i1}styk stylistyczny (\i1+varphi +1)\i0} 
. Ponieważ te dwa wskaźniki są równe, to prawda:
φ = φ + 1 φ φ {\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}{\i1}
Jednym ze sposobów na napisanie tego numeru jest
φ = 1 + 5 2 {\i1}displaystyle \i0}varphi ={\i0}frac {\i1+{\i1}sqrt {\i0}}{\i1}
5
{\i1}jest jak każda liczba, która po pomnożeniu przez siebie, daje 5 (lub która liczba jest mnożona): 5 × 5 = 5 {\i1}
Złota proporcja to nieracjonalna liczba. Jeśli ktoś spróbuje ją napisać, to nigdy się nie zatrzyma i nigdy nie utworzy wzoru, ale zacznie się w ten sposób: 1.6180339887... Ważną rzeczą w tej liczbie jest to, że dana osoba może odjąć od niej 1 lub podzielić przez nią 1. Tak czy inaczej, liczba ta będzie się powtarzać i nigdy się nie zatrzyma.
Złoty prostokąt
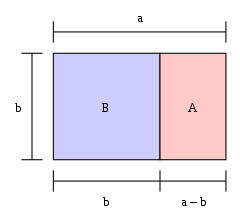
Jeżeli długość prostokąta podzielona przez jego szerokość jest równa złotemu stosunkowi, to prostokąt ten jest "złotym prostokątem". Jeżeli kwadrat jest odcięty od jednego końca złotego prostokąta, to drugi jego koniec jest nowym złotym prostokątem. Na zdjęciu, duży prostokąt (niebieski i różowy razem) jest złotym prostokątem, ponieważ a / b = φ {\i1}styk a/b=\i0}varphi } 
. Niebieska część (B) jest kwadratem. Różowa część (A) sama w sobie jest kolejnym złotym prostokątem, ponieważ b / ( a - b ) = φ {\i1}styk b/(a-b)=\i0}varphi } 
. Duży prostokąt i różowy prostokąt mają tę samą formę, ale różowy prostokąt jest mniejszy i jest obrócony.
Duży prostokąt BA jest złotym prostokątem, to znaczy, proporcja b:a wynosi 1: φ {\i0}displaystyle \i0}varphi \i0} . Dla każdego takiego prostokąta, i tylko dla prostokątów o tej konkretnej proporcji, jeśli usuniemy kwadrat B, to co zostanie, A, jest kolejnym złotym prostokątem, czyli o tych samych proporcjach, co pierwotny prostokąt.
Numery Fibonacciego
Numery Fibonacciego to lista numerów. Osoba może znaleźć następny numer na liście poprzez dodanie dwóch ostatnich numerów razem. Jeśli dana osoba podzieli liczbę na liście przez liczbę, która pojawiła się przed nią, stosunek ten jest coraz bliższy złotemu.
| Numer Fibonacciego | podzielony przez tego, który wcześniej | Stosunek: |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\i1}Displastyle {\i1}varphi?{\i0} | = 1.6180... |
Złota proporcja w przyrodzie
W przyrodzie, złoty stosunek jest często używany do układania liści lub kwiatów. Wykorzystują one złoty kąt około 137,5 stopnia. Liście lub kwiaty ułożone pod tym kątem najlepiej wykorzystują światło słoneczne.
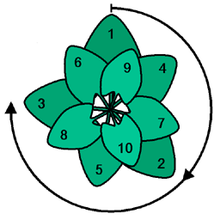
Użycie złotego kąta optymalnie wykorzysta światło słoneczne. Jest to widok z góry.
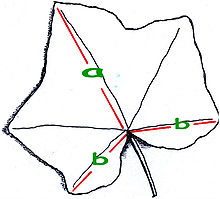
Liść bluszczu pospolitego, wykazujący złotą proporcję
Pytania i odpowiedzi
P: Jaki jest stosunek dwóch liczb?
O: Stosunek dwóch liczb znajduje się przez ich podzielenie, więc stosunkiem będzie a/b.
P: Jak można znaleźć inny stosunek?
O: Inny stosunek można znaleźć, dodając obie liczby do siebie, a następnie dzieląc tę sumę przez większą liczbę, a. Ten nowy stosunek będzie wynosił (a+b)/a.
P: Jak się nazywa sytuacja, w której te dwa stosunki są sobie równe?
O: Kiedy te dwa współczynniki są sobie równe, nazywa się to złotą proporcją. Zazwyczaj przedstawia się ją grecką literą צ lub phi.
P: Jeżeli b = 1 i a/b = צ , to co to oznacza dla a?
O: Jeżeli b = 1 i a/b = צ , to znaczy, że a = צ również.
P: Jak można zapisać tę liczbę?
O: Jednym ze sposobów zapisania tej liczby jest צ = 1 + 5 / 2 = 1,618...
P: Co to znaczy, że odejmuje Pan od niej 1 lub dzieli przez nią 1?
O: Jeżeli odejmie Pan od niej 1 lub podzieli przez nią 1, otrzyma Pan z powrotem tę samą liczbę - innymi słowy, obie będą równe złotej proporcji.
P: Czy złota proporcja jest liczbą irracjonalną?
O: Tak, złota proporcja jest liczbą irracjonalną, co oznacza, że jeśli ktoś spróbuje ją zapisać, to nigdy nie będzie końca i nie będzie wzoru - tylko zacznie się od czegoś w rodzaju "1,6180339887...".
