Przestrzeń probabilistyczna
Przestrzeń prawdopodobieństwa to model matematyczny używany do opisu eksperymentów naukowych Przestrzeń prawdopodobieństwa składa się z trzech części:
- Przykładowa przestrzeń, która zawiera listę wszystkich możliwych wyników
- Zestaw wydarzeń. Każde zdarzenie wiąże się z zerem lub większą liczbą wyników
- Funkcja, która przypisuje prawdopodobieństwa do każdego zdarzenia
Wynik jest wynikiem pojedynczego wykonania modelu. Ponieważ pojedyncze wyniki mogą mieć niewielkie praktyczne zastosowanie, do charakterystyki grup wyników stosuje się bardziej złożone zdarzenia. Zbiór wszystkich takich zdarzeń jest σ-algebra F {\i1}w stylu skryptowym {\i0}. 
. Wreszcie, istnieje potrzeba określenia prawdopodobieństwa wystąpienia każdego zdarzenia. Dokonuje się tego za pomocą funkcji pomiaru prawdopodobieństwa, P.
Po ustaleniu przestrzeni prawdopodobieństwa przyjmuje się, że "natura" wykonuje swój ruch i wybiera jeden wynik, ω, z przestrzeni próbkowania Ω. Wszystkie zdarzenia w F {\i1}stylu graficznym {\i1}, które zawierają wybrany wynik ω (pamiętaj, że każde zdarzenie jest podzbiorem Ω) są uważane za "zaistniałe". Wyboru dokonywanego z natury dokonuje się w taki sposób, że gdyby eksperyment miał być powtarzany nieskończoną ilość razy, to względne częstotliwości występowania każdego ze zdarzeń pokrywałyby się z prawdopodobieństwami określonymi przez funkcję P.
Wybitny radziecki matematyk Andriej Kołmogorow wprowadził w latach trzydziestych XX wieku pojęcie przestrzeni prawdopodobieństwa wraz z innymi aksjomatami prawdopodobieństwa.
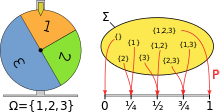
Modelowanie koła fortuny z wykorzystaniem przestrzeni prawdopodobieństwa
Pytania i odpowiedzi
P: Co to jest przestrzeń prawdopodobieństwa?
O: Przestrzeń prawdopodobieństwa to model matematyczny służący do opisu eksperymentów naukowych. Składa się z trzech części: przestrzeni prób, w której wymienione są wszystkie możliwe wyniki, zbioru zdarzeń, które wiążą się z zerowym lub większym wynikiem, oraz funkcji, która przypisuje prawdopodobieństwo każdemu zdarzeniu.
P: Z czego składa się przestrzeń prób?
O: Przestrzeń próbek składa się z wszystkich możliwych wyników, często zapisywanych jako Ω {Omega } oraz wynik jako ω { {omega }. .
P: Co to jest wynik?
O: Wynik to rezultat pojedynczego wykonania modelu.
P: Do czego służą zdarzenia w przestrzeni prawdopodobieństwa?
O: Zdarzenia służą do charakteryzowania grup wyników, ponieważ pojedyncze wyniki mogą być mało przydatne w praktyce. Zbiór wszystkich takich zdarzeń nazywamy σ-algebrą, czasami zapisywaną jako F {mathcal {F}}.
P: Jak przypisuje się prawdopodobieństwo do każdego zdarzenia?
O: Prawdopodobieństwo przypisuje się do każdego zdarzenia za pomocą funkcji miary prawdopodobieństwa P.
P: Kto wprowadził pojęcie przestrzeni prawdopodobieństwa? O: Wybitny matematyk radziecki Andrzej Kołmogorow wprowadził pojęcie przestrzeni prawdopodobieństwa wraz z innymi aksjomatami prawdopodobieństwa w latach 30-tych XX wieku.
