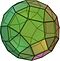
Wielościan półforemny
W geometrii bryła archimedesowa to kształt wypukły, który składa się z wielokątów. Jest to wielościan o następujących własnościach:
- Każda ściana jest zbudowana z wielokąta foremnego
- Wszystkie rogi kształtu wyglądają tak samo
- Kształt ten nie jest ani bryłą platońską, ani graniastosłupem, ani antygraniastosłupem.
W zależności od sposobu liczenia, takich kształtów jest trzynaście lub piętnaście. Z dwóch z tych brył istnieją dwie wersje, których nie da się uzgodnić za pomocą obrotu. Nazwa brył archimedesowych pochodzi od imienia starożytnego greckiego matematyka Archimedesa, który odkrył je prawdopodobnie w III wieku p.n.e.. Pisma Archimedesa zaginęły, ale Pappus z Aleksandrii streścił je w IV wieku. W okresie renesansu artyści i matematycy cenili czyste formy i odkryli je na nowo. Johannes Kepler prawdopodobnie zakończył te poszukiwania około 1620 roku.
Do skonstruowania bryły archimedesowej potrzeba co najmniej dwóch różnych wielokątów.
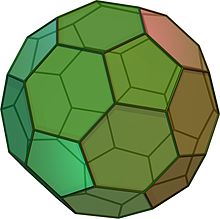
Ikozaedr ścięty wygląda jak piłka nożna. Zbudowany jest z 12 pięciokątów równobocznych i 20 sześciokątów foremnych. Ma 60 wierzchołków i 90 krawędzi. Jest to bryła Archimedesowa.
Właściwości
- Bryły archimedesowe zbudowane są z wielokątów foremnych, dlatego wszystkie krawędzie mają tę samą długość.
- Wszystkie bryły archimedesowe można otrzymać z brył platońskich przez "przecięcie krawędzi" bryły platońskiej.
- Typ wielokątów spotykających się w kącie ("wierzchołku") charakteryzuje zarówno bryłę archimedesową jak i platońską
Związek z bryłami platońskimi
Bryły platońskie można przekształcić w bryły archimedesowe, stosując się do szeregu reguł ich budowy.
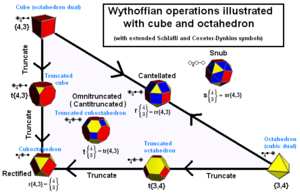
Bryły Archimedesowe mogą być skonstruowane jako pozycje generatorów w kalejdoskopie
Zestawienie brył archimedesowych
Poniżej znajduje się zestawienie wszystkich brył archimedesowych
| Obraz | Nazwa | Twarze | Typ | Krawędzie | Wierzchołki |
|
| Ścięty czworościan foremny | 8 | 4 trójkąty 4 sześciokąty | 18 | 12 |
|
| 14 | 8 trójkątów 6 kwadratów | 24 | 12 | |
|
| Sześcian ścięty | 14 | 8 trójkątów 6 ośmiokątów | 36 | 24 |
|
| Ośmiościan ścięty | 14 | 6 kwadratów 8 sześciokątów | 36 | 24 |
|
| Rombikuboktaedr | 26 | 8 trójkątów 18 kwadratów | 48 | 24 |
|
| Ścięty prostopadłościan | 26 | 12 kwadratów 8 sześciokątów 6 ośmiokątów | 72 | 48 |
|
| Snub cube (2 wersje lustrzane) | 38 | 32 trójkąty 6 kwadratów | 60 | 24 |
|
| Icosidodecahedron | 32 | 20 trójkątów 12 pięciokątów | 60 | 30 |
|
| Dodekaedr ścięty | 32 | 20 trójkątów 12 dekad | 90 | 60 |
|
| Ścięty dwudziestościan foremny | 32 | 12 pięciokątów 20 sześciokątów | 90 | 60 |
|
| Rómbikosidodekanatron | 62 | 20 trójkątów30 kwadratów12 | 120 | 60 |
|
| Ścięty dwudziestościan foremny (icosidodecahedron) | 62 | 30 kwadratów 20 sześciokątów 12 dekad | 180 | 120 |
|
| Dodekaedron ścięty (2 wersje lustrzane) | 92 | 80 trójkątów 12 pięciokątów | 150 | 60 |
Pytania i odpowiedzi
P: Co to jest bryła archimedesowa?
O: Bryła archimedesowa to wypukły kształt zbudowany z wielokątów, który ma takie własności, że każda ściana jest wielokątem foremnym, wszystkie rogi mają taki sam wygląd i nie jest bryłą platońską, graniastosłupem ani antypryzmatem.
P: Ile jest brył archimedesowych?
O: W zależności od sposobu liczenia, istnieje trzynaście lub piętnaście brył archimedesowych.
P: Kto odkrył bryły archimedesowe?
O: Nazwa brył Archimedesa pochodzi od nazwiska starożytnego greckiego matematyka Archimedesa, który odkrył je prawdopodobnie w III wieku p.n.e.
P: Co zrobił Pappus z Aleksandrii z pismami Archimedesa?
O: Pappus z Aleksandrii streścił w IV wieku pisma Archimedesa dotyczące brył Archimedesa.
P: Dlaczego artyści i matematycy odkryli na nowo bryły Archimedesa w okresie renesansu?
O: W okresie renesansu artyści i matematycy cenili czyste formy, a bryły Archimedesa były uważane za czyste formy.
P: Kiedy Johannes Kepler zakończył poszukiwania wszystkich brył archimedesowych?
O: Johannes Kepler zakończył poszukiwania wszystkich brył archimedesowych prawdopodobnie około 1620 roku.
P: Co jest potrzebne do skonstruowania bryły archimedesowej?
O: Skonstruowanie bryły archimedesowej wymaga co najmniej dwóch różnych wielokątów.
Przeszukaj encyklopedię