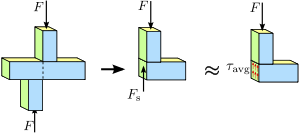Naprężenie: definicja, wzór i jednostki (Pa, psi) w mechanice
Naprężenie: definicja, wzór i jednostki (Pa, psi) — praktyczne wyjaśnienie pojęcia, obliczeń i zastosowań w mechanice continuum. Wzory, przykłady, konwersje.
Naprężenie to siła przypadająca na jednostkę powierzchni materiału, która powoduje dążenie do zmiany jego kształtu lub objętości. Jest to miara wewnętrznych sił między cząstkami ciała, wynikających z działania sił zewnętrznych (np. obciążenia zewnętrznego, ciśnienia powierzchniowego). Napięcie przedstawia średnią siłę, jaką jedna część materiału wywiera na sąsiednią przez wyimaginowaną powierzchnię rozdzielającą te części.
Wzór i podstawowa jednostka
W najprostszym, jednoosiowym przypadku naprężenie normalne (prostopadłe do powierzchni) definiuje się jako stosunek siły do pola przekroju:
σ = F A {\i1}Displaystyle {\i0}== Frac {\i1}{\i1}(A)}
gdzie σ jest naprężeniem, F — siłą działającą na powierzchnię, a A — polem tej powierzchni. Dla naprężenia ścinającego używa się analogicznie symbolu τ i siły stycznej do powierzchni.
W jednostkach SI siła mierzy się w niutonach (N), pole powierzchni w metrach kwadratowych (m²). Stąd jednostką naprężenia jest N/m², która ma własną nazwę: paskal (Pa). 1 Pa = 1 N/m². Częściej używane praktyczne jednostki to MPa (megapaskal = 10⁶ Pa) i GPa (gigapaskal = 10⁹ Pa).
W jednostkach Imperial naprężenie bywa podawane jako funty siły na cal kwadratowy (lbf/in²), zwykle skracane do „psi”. Przybliżone przeliczenie: 1 psi ≈ 6894,76 Pa.
Wymiar fizyczny
Wymiar naprężenia jest taki sam jak wymiar ciśnienia: M·L⁻¹·T⁻². Naprężenie jest więc wielkością tensyjną o tej samej jednostce co ciśnienie, mimo że mechanicznie opisuje różne zjawiska (rozkład sił wewnątrz ciała vs. ciśnienie w gazie/cieczy).
Rodzaje naprężeń
- Naprężenie normalne (σ) — działa prostopadle do rozważanej powierzchni (np. rozciąganie, ściskanie).
- Naprężenie ścinające (τ) — działa równolegle do powierzchni (np. ścinanie warstw materiału).
- Naprężenie wieloosiowe — w ogólnym trójwymiarowym stanie naprężeń opisujemy tensorem naprężeń σij (macierz 3×3), gdzie na przekątnej są naprężenia normalne, a poza przekątną komponenty ścinające.
- Naprężenia główne — wartości własne tensora naprężeń, dla których komponenty ścinające zanikałyby w układzie współrzędnych; użyteczne przy analizie wytrzymałościowej.
Znaki i konwencje
Stosowane są różne konwencje znaków; najczęściej przyjmuje się, że rozciąganie daje dodatnie naprężenie, a ściskanie ujemne. Ważne jest konsekwentne stosowanie przyjętej konwencji w obliczeniach inżynierskich.
Naprężenie w mechanice kontinuum
W mechanice kontinuum materiał traktuje się jako ciągłe medium, więc wewnętrzne siły są rozłożone w sposób ciągły w całej objętości. Rozkład naprężeń zależy od położenia i czasu i zwykle opisuje się go funkcją σ(x,t). Naprężenia są powiązane z odkształceniami przez równania konstytutywne (np. prawo Hooke’a dla sprężystych materiałów liniowych), co pozwala przejść od znanej deformacji do odpowiednich naprężeń:
σ = C : ε (ogólnie tensora sprężystości C działający na tensor odkształcenia ε).
Pomiar i znaczenie praktyczne
- Pomiar: naprężenia w konstrukcjach mierzy się najczęściej przy pomocy tensometrów (strain gauges), które mierzą odkształcenia, a następnie przelicza się je na naprężenia korzystając z modułu sprężystości materiału.
- Wytrzymałość: materiał jest projektowany tak, aby maksymalne naprężenia nie przekroczyły granicy plastyczności lub niszczenia (np. wytrzymałość na rozciąganie, granica plastyczności).
- Analiza numeryczna: w praktyce inżynierskiej rozkład naprężeń w skomplikowanych elementach oblicza się metodą elementów skończonych (MES/FEM).
Przykłady
- Jeśli na pręt o polu przekroju A = 10 mm² działa siła F = 1000 N osiowo rozciągająca, to σ = F/A = 1000 N / (10×10⁻⁶ m²) = 100×10⁶ Pa = 100 MPa.
- Ciśnienie w oponie (np. 2 bar ≈ 0,2 MPa) jest także naprężeniem dla wewnętrznej ściany opony, choć w praktyce analizuje się złożone stany naprężeń.
Krótko o kryteriach zniszczenia
Aby ocenić, czy materiał lub konstrukcja bezpiecznie wytrzyma obciążenie, stosuje się kryteria wytrzymałościowe: np. kryterium Kirchhoffa, Tresca, czy bardziej rozpowszechnione kryterium von Misesa, które porównuje równoważne naprężenie z granicą plastyczności materiału.
Podsumowanie: Naprężenie to kluczowa wielkość mechaniki materiałów i mechaniki konstrukcji — opisuje, jak duże wewnętrzne siły działają wewnątrz ciała na jednostkę powierzchni. Prawidłowe określenie rozkładu naprężeń i porównanie go z własnościami materiału pozwala projektować bezpieczne i ekonomiczne konstrukcje.
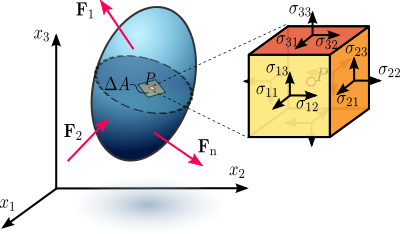
Rys. 1.1 Naprężenia w obciążonym, odkształcalnym materialnym korpusie założonym jako kontinuum.
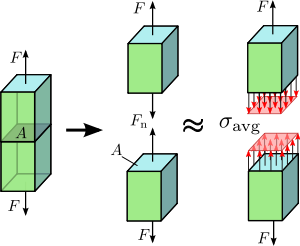
Rysunek 1.2 Naprężenie osiowe w pręcie pryzmatycznym obciążonym osiowo.
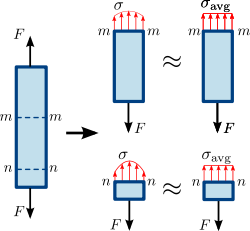
Rys. 1.3 Naprężenie normalne w pręcie pryzmatycznym (prostym o jednolitym przekroju poprzecznym). Naprężenia lub rozkład sił w przekroju poprzecznym pręta nie muszą być równomierne. Jednakże średnie naprężenie normalne σ a v g {\i0}sigma {\i0}mathrm {avg} }\,\! {y:
Rys. 1.4 Naprężenie ścinające w pręcie pryzmatycznym. Rozkład naprężeń lub siły w przekroju poprzecznym pręta nie musi być jednolity. Niemniej jednak, średnie naprężenie ścinające τ a v g {\i0}naprętem pryzmatycznym nie jest równomierne. }\,\! {y:
Stres ścinający
Dalsze informacje: Stres ścinający
Proste naprężenia
W niektórych sytuacjach stres wewnątrz obiektu może być opisany za pomocą jednej liczby lub jednego wektora (liczby i kierunku). Trzy takie proste sytuacje stresowe to jednoosiowy stres normalny, prosty stres ścinający i izotropowy stres normalny.
Unijny stres normalny
Naprężenie rozciągające (lub rozciąganie) jest stanem naprężenia prowadzącym do wydłużenia; to znaczy, że długość materiału ma tendencję do zwiększania się w kierunku rozciągania. Objętość materiału pozostaje stała. Gdy na ciało działają równe i przeciwstawne siły, wówczas naprężenie spowodowane tą siłą nazywane jest naprężeniem rozciągającym.
Dlatego w materiale jednoosiowym długość zwiększa się w kierunku naprężenia rozciągającego, a pozostałe dwa kierunki zmniejszają się. W jednoosiowym sposobie rozciągania, naprężenie rozciągające jest indukowane przez siły rozciągające. Naprężenie rozciągające jest przeciwieństwem naprężenia ściskającego.
Elementami konstrukcyjnymi poddawanymi bezpośredniemu rozciąganiu są liny, kotwy gruntowe i gwoździe, śruby itp. Belki narażone na działanie momentów zginających mogą zawierać naprężenia rozciągające, jak również naprężenia ściskające i/lub ścinające.
Naprężenie rozciągające może być zwiększone aż do osiągnięcia wytrzymałości na rozciąganie, czyli stanu granicznego naprężenia.
Stres w ciałach jednowymiarowych
Wszystkie prawdziwe obiekty zajmują trójwymiarową przestrzeń. Jeśli jednak dwa wymiary są bardzo duże lub bardzo małe w porównaniu z innymi, obiekt może być modelowany jako jednowymiarowy. Upraszcza to modelowanie matematyczne obiektu. Do obiektów jednowymiarowych zalicza się kawałek drutu załadowany na końcach i oglądany z boku oraz blachę metalową załadowaną na powierzchnię czołową i oglądaną z bliska i przez przekrój poprzeczny.
Powiązane strony
- Napięcie
- Gięcie
Pytania i odpowiedzi
P: Co to jest naprężenie?
O: Naprężenie to siła działająca na jednostkę powierzchni ciała, która powoduje zmianę jego kształtu. Jest to miara sił wewnętrznych w ciele pomiędzy jego cząstkami i jest to średnia siła na jednostkę powierzchni, jaką cząstka ciała wywiera na sąsiednią cząstkę na wyimaginowanej powierzchni, która je dzieli.
P: Jak siły zewnętrzne wpływają na naprężenia?
O: Siły zewnętrzne są albo siłami powierzchniowymi, albo siłami ciała i powodują odkształcenie kształtu ciała, co może prowadzić do trwałej zmiany kształtu lub uszkodzenia konstrukcji, jeżeli materiał nie jest wystarczająco mocny.
P: Jaki jest wzór na jednoosiowe naprężenie normalne?
O: Wzór na jednoosiowe naprężenie normalne to σ = F/A, gdzie σ to naprężenie, F to siła, a A to pole powierzchni. W jednostkach układu SI siłę mierzy się w niutonach, a powierzchnię w metrach kwadratowych, co oznacza, że naprężenie byłoby równe niutonom na metr kwadratowy (N/m2). Istnieje jednak własna jednostka SI dla naprężeń zwana paskal (Pa), która jest równa 1 N/m2. W jednostkach imperialnych naprężenie byłoby mierzone w funtach na cal kwadratowy (psi).
P: Co mechanika kontinuum zakłada na temat siły?
O: Klasyczne modele mechaniki kontinuum zakładają średnią siłę i nie uwzględniają właściwie czynników geometrycznych - to znaczy nie biorą pod uwagę tego, jak geometria wpływa na gromadzenie się energii podczas działania siły zewnętrznej.
P: Jak to się dzieje, że różne modele dają różne wyniki w przypadku deformacji materii i ciał stałych?
O: Różne modele różnie patrzą na deformację materii i ciał stałych, ponieważ właściwości materii i ciał stałych są trójwymiarowe - dlatego każde podejście uwzględnia inne aspekty, co może prowadzić do różnych wyników.
P: Jak mechanika continuum traktuje obciążone ciała odkształcalne?
O: Mechanika kontinuum traktuje obciążone ciała odkształcalne jako kontinua - co oznacza, że siły wewnętrzne są rozłożone w sposób ciągły w objętości ciała materialnego, a nie skoncentrowane w pewnych punktach, jak w modelach klasycznych.
Przeszukaj encyklopedię