Suma kontrolna
Suma kontrolna to liczba. Jest to rodzaj kontroli nadmiarowej. Są różne sposoby jej obliczania. Służy ona do sprawdzenia, czy przy zapisie liczby nie popełniono żadnych błędów. W najprostszej formie, cyfry są po prostu sumowane. Nie pozwala to jednak na wykrycie błędów związanych z zamianą cyfr wokół. Lepszymi sposobami (algorytmami) obliczenia sumy kontrolnej jest użycie kodu Hamminga, cyklicznej kontroli nadmiarowości lub modułowej arytmetyki. Jednym z zastosowań sum kontrolnych jest sprawdzenie, czy numery kont zostały wprowadzone poprawnie.
Portugalskie identyfikatory kont bankowych są dobrym przykładem działania sum kontrolnych. Mają one 21 cyfr. Pierwsze 19 cyfr identyfikuje bank, oddział i numer konta. Dwie ostatnie cyfry to cyfry sumy kontrolnej "mod 97" oparte na arytmetyce modułowej. Typowy portugalski numer rachunku bankowego to 0002.0123.12345678901.54. Cyfry te mają następujące znaczenia:
· Cyfry "0002" reprezentują bank.
· Cyfry "0123" oznaczają oddział banku.
· Cyfry "12345678901" oznaczają numer rachunku.
· Cyfry "54" reprezentują sumę kontrolną.
Jeśli 000201231234567890154 (numer rachunku bankowego bez punktów) zostanie podzielony przez 97, to odpowiedź brzmi 207458809978249, w pozostałej części 1. Ponieważ pozostała część to "1", to prawdopodobnie identyfikator rachunku bankowego jest poprawny. Gdyby osoba zapisująca numer pominęła jakąś cyfrę, zamieniła dwie cyfry dookoła lub zapisała błędnie jakąś cyfrę, to reszta nie byłaby "1". Jeśli tak, to komputer powinien wykryć błąd i podać komunikat o błędzie.
Innym miejscem, w którym wykorzystywane są sumy kontrolne, są numery seryjne oprogramowania komputerowego.
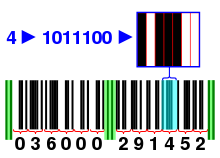
Nowoczesny kod kreskowy EAN: Części w kolorze zielonym nazywane są przekładkami: Oddzielają one grupy numerów. Każdy numer jest zakodowany za pomocą 7 bitów, jak pokazano na rysunku. Pierwsze 11 cyfr oznacza numer produktu. Ostatnią cyfrą, w tym przypadku liczbą "2", jest suma kontrolna. Suma kontrolna jest dodawana w ten sposób, że suma pozycji parzystych i nieparzystych pomnożona przez trzy, modulo 10 wynosi 0.
Pytania i odpowiedzi
P: Co to jest suma kontrolna?
O: Suma kontrolna to liczba wykorzystywana do sprawdzania nadmiarowości. Służy do sprawdzenia, czy podczas zapisywania numeru nie popełniono błędów.
P: Jak oblicza się sumy kontrolne?
O: Sumy kontrolne można obliczać na różne sposoby, ale w najprostszej formie cyfry są po prostu sumowane. W ten sposób nie można jednak wykryć błędów polegających na zamianie cyfr.
P: Jaki jest przykład działania sum kontrolnych?
O: Dobrym przykładem działania sum kontrolnych są portugalskie identyfikatory kont bankowych. Mają one 21 cyfr, a dwie ostatnie cyfry stanowią sumę kontrolną "mod 97", opartą na arytmetyce modułowej.
P: Jak to pomaga w wykrywaniu błędów?
O: Jeżeli jakaś cyfra zostanie pominięta, zamieniona lub źle zapisana, to reszta nie będzie "1". W takim przypadku komputer powinien wykryć błąd i podać informację o błędzie.
P: Gdzie jeszcze stosuje się sumy kontrolne?
O: Sumy kontrolne są również stosowane w numerach seryjnych oprogramowania komputerowego.
P: Co się stanie, jeżeli suma kontrolna wykryje błąd?
O: Jeżeli suma kontrolna wykryje błąd, to komputer powinien go wykryć i podać komunikat o błędzie.
