Geometria Wszechświata: kształt, topologia i dowody obserwacyjne

Geometria Wszechświata: odkryj kształt, topologię i dowody obserwacyjne — od krzywizny po najnowsze pomiary potwierdzające płaskość kosmosu.

Autor: Leandro Alegsa

13-02-2026 22:26

Kształt Wszechświata nie może być omawiany z codziennymi terminami, ponieważ wszystkie terminy muszą być względami einsteinowskimi. Geometria Wszechświata nie jest więc zwykłą euklidesową geometrią naszego codziennego życia.

Zgodnie ze szczególną teorą względności nie można stwierdzić, czy dwa odrębne zdarzenia zachodzą w tym samym czasie, jeśli zdarzenia te są rozdzielone w przestrzeni. Mówienie o "kształcie wszechświata (w danym momencie)" jest naiwne z punktu widzenia szczególnej względności. Ze względu na relatywność jednoczesności nie możemy mówić o różnych punktach w przestrzeni jako o "tym samym punkcie w czasie", a zatem o "kształcie wszechświata w punkcie czasowym".

To, co robią astrofizycy, to pytanie, czy dany model wszechświata jest zgodny z tym, co jest znane z obserwacji i pomiarów wszechświata. Jeśli obserwowalny wszechświat jest mniejszy od całego wszechświata (w niektórych modelach jest o wiele rzędów wielkości mniejszy lub nawet nieskończony), obserwacja ogranicza się do części całości.

Rozważania na temat kształtu wszechświata można podzielić na dwa:

geometria lokalna, która odnosi się szczególnie do krzywizny wszechświata, zwłaszcza we wszechświecie obserwowalnym, oraz
geometria globalna, która odnosi się do topologii wszechświata jako całości, której pomiar może nie być możliwy.

Obserwowalny wszechświat jest podstawą do testowania każdego modelu wszechświata. Jest to kulista objętość (kula) skupiona na obserwatorze, niezależnie od kształtu wszechświata jako całości. Każda lokalizacja we wszechświecie ma swój własny obserwowalny wszechświat, który może, ale nie musi pokrywać się z tym, który jest wyśrodkowany na Ziemi.

Ostatnie pomiary doprowadziły NASA do stwierdzenia: "Teraz wiemy, że wszechświat jest płaski z tylko 0,4% marginesem błędu". W ramach jednego modelu, modelu FLRW, najpopularniejszym obecnie kształtem Wszechświata, który pasuje do danych obserwacyjnych, jest nieskończenie płaski model. Istnieją inne modele, które również pasują do danych.

Geometria lokalna — krzywizna przestrzeni

Geometria lokalna opisuje, jak przestrzeń wygląda w małych (lokalnych) skalach i jest określona przez krzywiznę przestrzeni. W kontekście kosmologicznym rozróżniamy trzy podstawowe typy krzywizny przestrzennej:

Krzywizna dodatnia — odpowiada przestrzeni zamkniętej (analogia: powierzchnia kuli w 2D). W prostych modelach jest to tzw. trójwymiarowa sfera (3-sfera) o skończonej objętości.
Krzywizna zerowa — przestrzeń płaska (euklidesowa) na dużą skalę; równoległe proste pozostają równoległe, suma kątów w trójkącie wynosi 180°.
Krzywizna ujemna — przestrzeń hiperboliczna (otwarta), w której geometria różni się od euklidesowej (trójkąty mają sumę kątów mniejszą niż 180°).

W praktyce krzywiznę mierzy się za pomocą parametru krzywizny przestrzennej, często zapisywanego jako Ω_k (albo poprzez stałą krzywizny k). W modelach FLRW wielkości takie jak gęstość materii, prędkość ekspansji (Hubble'a) i energii ciemnej determinują efektywnie geometryczną postać metryki.

Promień krzywizny (czyli skala, na której odchylenia od płaskości stają się istotne) można oszacować prostym wzorem porównawczym: R_c ≈ c / (H0 · sqrt(|Ω_k|)), gdzie c to prędkość światła, a H0 stała Hubble’a. Dla bardzo małego |Ω_k| promień krzywizny jest bardzo duży — znacznie większy od obserwowalnego wszechświata.

Geometria globalna — topologia

Topologia dotyczy kształtu przestrzeni jako całości — czy jest ona skończona czy nieskończona, czy ma strukturę wielokrotnie połączoną (multiply connected) itp. Topologia nie jest wprost równoważna krzywiźnie: przestrzeń o zerowej krzywiźnie może być nieskończona (standardowa przestrzeń euklidesowa) lub skończona (np. trójwymiarowy torus, powstały przez "sklejanie" przeciwległych ścian sześcianu).

Przykłady topologii, które bywały rozważane:

3-sfera (zamknięta i skończona) — związana z dodatnią krzywizną.
3-torus (trójwymiarowy torus) — płaski, ale skończony i wielokrotnie połączony.
Przestrzenie hiperboliczne o złożonych topologiach — mogą być skończone mimo ujemnej krzywizny.

Topologia może pozostawić obserwowalne ślady, np. powtarzające się obrazy odległych struktur (wielokrotne obrazy tej samej galaktyki z różnych "kierunków") lub specyficzne korelacje w mikrofalowym promieniowaniu tła (CMB), jak zasugerowane niegdyś hipotezy o "dodekaedrycznej" topologii. Do dziś jednak nie znaleziono przekonujących dowodów na powtarzalność wzorców o skali mniejszej niż rozmiar obserwowalnego wszechświata.

Dowody obserwacyjne i metody pomiaru

Obserwacje pozwalają odróżnić (i ograniczyć) możliwe geometrie i topologie. Główne metody to:

Mikrofalowe promieniowanie tła (CMB) — analiza anisotropii i położenia pierwszego z wielu akustycznych piku w spektrum kątowym pozwala precyzyjnie wyznaczyć geometrię przestrzeni na dużej skali. Pozycja pierwszego piku jest szczególnie czuła na ogólną krzywiznę.
Oscylacje akustyczne barionów (BAO) — standardowa skala długości w rozkładzie galaktyk, porównywana z przewidywaniami modeli kosmologicznych, daje informacje o geometrii i ekspansji wszechświata.
Supernowe typu Ia — jako mierniki odległości (standardowe świece) pozwalają badać zależności jasność–czerwone przesunięcie i w konsekwencji krzywiznę/rozwój ekspansji.
SOCZEWKOWANIE grawitacyjne i duże struktury — soczewkowanie słabe i analiza struktury wielkoskalowej dostarczają dodatkowych ograniczeń na parametry kosmologiczne.
Poszukiwanie efektów topologicznych — m.in. metoda "matched circles" (szukanie pasujących okręgów w CMB), analiza powtarzalnych wzorców w rozmieszczeniu obiektów, które występują przy wielokrotnym połączeniu przestrzeni.

Połączenie tych metod (CMB + BAO + SNe + lensering) w ramach modelu ΛCDM daje obecnie bardzo silne ograniczenia: przestrzeń jest zgodna z byciem płaską z niepewnością na poziomie co najwyżej części promila do promila rzędu 10^-3–10^-2 w parametrze Ω_k (co odpowiadać może często cytowanym wartościom rzędu 0,1–0,5% płaskości). Różne zestawy danych i metody dają nieco różne dokładności, ale konsensus jest taki, że nie ma statystycznie istotnego odchylenia od płaskości.

Horyzonty, układy odniesienia i "teraz" w kosmologii

Pojęcie obserwowalnego wszechświata jako kuli wokół obserwatora wynika z istnienia horyzontu cząstek — maksymalnej odległości, z której światło miało czas do nas dotrzeć od początku ekspansji. W praktyce promień obserwowalnego wszechświata (w odległościach komowych) wynosi dziś około 46 miliardów lat świetlnych, mimo że wiek wszechświata to ~13,8 miliarda lat — różnica wynika z ekspansji przestrzeni.

Chociaż szczególna teoria względności odbiera absolutny sens jednoczesności, w kosmologii praktycznie wprowadza się naturalną foliację czasową związaną z czasem kosmicznym i układem obserwatorów komowych (poruszających się z ekspansją Hubble’a). Dla takich obserwatorów można mówić o "chwili" (powierzchniach stałego czasu kosmicznego) i definiować "kształt przestrzeni w danym czasie kosmicznym". To ułatwia porównywanie modeli z danymi obserwacyjnymi.

Ograniczenia i otwarte pytania

Mimo wysokiej precyzji pomiarów kilka istotnych kwestii pozostaje otwartych:

Możliwa, ale mała, krzywizna lub niestandardowa topologia ukryta na skalach większych od obserwowalnego wszechświata — w takim przypadku żadna obserwacja wewnątrz naszego horyzontu nie pozwoli tego stwierdzić bezpośrednio.
Systematyki i napięcia pomiędzy różnymi pomiarami parametrów kosmologicznych (np. obecne napięcie wartości H0 z różnych metod) mogą wpływać na wyciągane wnioski o geometrii w przyszłości.
Hipotezy bardziej egzotyczne (np. lokalne aniotropie, przejścia fazowe wpływające na globalny kształt) wymagają dalszych badań i nowych obserwacji.

Wnioski

Podsumowując: obserwacje wskazują, że lokalna geometria Wszechświata jest z dużą precyzją zbliżona do płaskiej. Globalna topologia pozostaje mniej ograniczona — wiele konfiguracji jest wciąż dopuszczalnych, gdy ich skale charakterystyczne przekraczają rozmiar obserwowalnego wszechświata. Dalsze, coraz dokładniejsze pomiary CMB, BAO, soczewkowania oraz przeglądy galaktyk będą dalej zawężać możliwe scenariusze i mogą kiedyś ujawnić ślady nietrywialnej topologii lub drobnych odchyleń od płaskości.

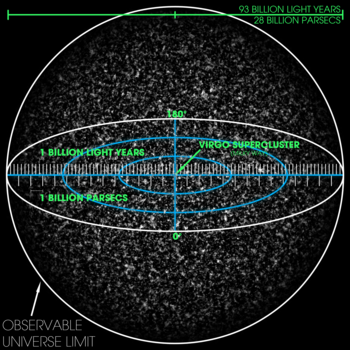
Wizualizacja 93 miliardów lat świetlnych - czyli 28 miliardów parseksu - trójwymiarowego obserwowalnego wszechświata. Skala jest taka, że drobne ziarna reprezentują kolekcje dużych ilości superklastrów. Panna Supercluster - dom Drogi Mlecznej - jest zaznaczona w centrum, ale jest zbyt mała, aby można ją było zobaczyć na obrazie.

Pytania i odpowiedzi

P: Jaki jest kształt wszechświata według obecnych obserwacji?

O: Według ostatnich pomiarów NASA stwierdziła, że wszechświat jest płaski z marginesem błędu wynoszącym zaledwie 0,4%.

P: Jak szczególna względność wpływa na nasze rozumienie kształtu wszechświata?

O: Z powodu względności równoczesności nie można stwierdzić, czy dwa różne zdarzenia występują w tym samym czasie, jeżeli te zdarzenia są oddzielone w przestrzeni. Oznacza to, że nie można mówić o różnych punktach w przestrzeni jako o "tym samym punkcie w czasie", a tym samym o "kształcie wszechświata w danym momencie".

P: Jakiego rodzaju geometrii używają astrofizycy, gdy omawiają kształt Wszechświata?

O: Astrofizycy używają względności Einsteina przy omawianiu i testowaniu modeli opisujących i przewidujących aspekty Wszechświata. Biorą również pod uwagę geometrię lokalną, która dotyczy w szczególności krzywizny, oraz geometrię globalną, która dotyczy topologii.

P: Czy każde miejsce we Wszechświecie jest częścią obserwowalnego wszechświata?

O: Tak, każde miejsce we Wszechświecie ma swój własny obserwowalny wszechświat, który może, ale nie musi pokrywać się z tym skupionym na Ziemi.

P: Co oznacza słowo "płaski" w odniesieniu do modelu opisującego/przewidującego aspekty Wszechświata?

O: W ramach jednego modelu, zwanego FLRW (Friedmann-Lemaître-Robertson-Walker), "płaski" odnosi się do nieskończonego płaskiego modelu, który najlepiej pasuje do danych obserwacyjnych. Oznacza to, że przestrzeń wydaje się jednolita bez względu na to, gdzie się patrzy, a w tym konkretnym modelu nie ma żadnych krzywych ani zagięć.

P: Czy oprócz nieskończenie płaskiego modelu FLRW istnieją inne modele, które pasują do danych obserwacyjnych?

O: Tak, oprócz nieskończenie płaskiego modelu FLRW istnieją inne modele, które również pasują do danych obserwacyjnych.

Przeszukaj encyklopedię