Postulat równoległości (piąty postulat Euklidesa) — definicja i znaczenie
Poznaj piąty postulat Euklidesa: definicję, dowody i znaczenie w geometrii euklidesowej i nieeuklidesowej — jasne wyjaśnienie dla uczniów i pasjonatów.
W geometrii postulat równoległości jest jednym z aksjomatów geometrii euklidesowej. Czasami nazywany jest również piątym postulatem Euklidesa, ponieważ jest piątym postulatem w Elementach Euklidesa.
Postulat ten mówi, że:
Jeśli przetniemy odcinek prostej dwiema prostymi, a dwa kąty wewnętrzne, które tworzą te proste, sumują się do mniej niż 180°, to te dwie proste w końcu się spotkają, jeśli przedłużymy je wystarczająco długo.
Dziedzina geometrii, która spełnia wszystkie aksjomaty Euklidesa, nazywana jest geometrią euklidesową. Geometrie, które nie spełniają wszystkich aksjomatów Euklidesa nazywamy geometrią nieeuklidesową.
Różne formułowania postulatu
Postulat Euklidesa występuje w kilku równoważnych formach, spośród których najbardziej znane to:
- Postulat Euklidesa (oryginalne sformułowanie) — cytowane powyżej stwierdzenie o sumie kątów wewnętrznych mniejszych niż 180°.
- Zasada Playfaira — przez punkt poza daną prostą przechodzi dokładnie jedna prosta równoległa do tej prostej. Jest to najczęściej używane współczesne sformułowanie równoważne postulatowi Euklidesa.
- Różne inne aksjomaty równoważne — na przykład: suma kątów trójkąta równa się 180°; istnieje podobieństwo trójkątów o dowolnych rozmiarach; stosunek odcinków w podobnych trójkątach jest zachowany itp.
Niezależność postulatu i historia
Przez ponad dwa tysiące lat matematycy próbowali dowieść piątego postulatu z pozostałych aksjomatów Euklidesa, uważając go za mniej naturalny i trudniejszy niż pozostałe. W pracy nad tym problemem pojawiło się wiele prób modyfikacji i dowodów — m.in. prace Saccheriego, Lambert'a i innych — jednak końcowy przełom nastąpił na początku XIX wieku.
Matematycy tacy jak János Bolyai, Nikolaj Łobaczewski i Bernhard Riemann wykazali, że można konsekwentnie rozważać geometrię, w której postulat równoległości nie obowiązuje, co doprowadziło do powstania geometrii nieeuklidesowych (hiperbolicznej i eliptycznej). Modele tych geometrii (np. model Beltramiego, model Poincarégo, model Kleina) pokazały, że piąty postulat jest niezależny od pozostałych aksjomatów Euklidesa — czyli nie można go dowieść ani zaprzeczyć korzystając jedynie z pozostałych aksjomatów.
Konsekwencje przyjęcia postulatu
Przyjęcie piątego postulatu ma dalekosiężne konsekwencje dla własności przestrzeni geometrycznej. W geometrii euklidesowej wynikają m.in.:
- Każdy trójkąt ma sumę kątów równą 180°.
- Istnieje dokładnie jedna prosta równoległa do danej prostej przechodząca przez punkt poza nią (zasada Playfaira).
- Wiele twierdzeń dotyczących podobieństwa trójkątów oraz zachowania proporcji odcinków jest prawdziwych.
- Równoległość jest relacją przechodnią i działania na prostych i kątach mają dobrze znane własności używane w geometrii analitycznej i euklidesowej geometrii przestrzeni.
Geometrie nieeuklidesowe — krótki opis
Gdy odrzucimy lub zmienimy piąty postulat, uzyskujemy alternatywne spójne systemy geometryczne:
- Geometria hiperboliczna (Lobaczewskiego–Bolyai): przez punkt spoza danej prostej przechodzi co najmniej więcej niż jedna prosta równoległa do tej prostej; suma kątów trójkąta jest mniejsza niż 180°.
- Geometria eliptyczna (Riemanna): nie istnieją proste równoległe; sumy kątów trójkątów są większe niż 180°; przykładem jest powierzchnia sfery z geodezyjnymi jako "prostymi".
Znaczenie matematyczne i praktyczne
Postulat równoległości miał i ma ogromne znaczenie dla rozwoju matematyki:
- Rozwiązanie problemu niezależności postulatu doprowadziło do powstania nowych działów matematyki — geometrii nieeuklidesowej oraz badań nad aksjomatyzacją teorii matematycznych.
- Modele nieeuklidesowe mają bezpośrednie zastosowanie w teorii względności Einsteina (geometria pseudo-Riemanna), gdzie geometria przestrzeni zależy od obecności masy i energii.
- Badania nad aksjomatyzacją geometrii wpłynęły na rozwój logiki matematycznej i teorii modeli.
Podsumowanie
Postulat równoległości jest kluczowym elementem, który wyróżnia geometrię euklidesową spośród innych geometrii. Choć na pierwszy rzut oka wygląda na intuicyjny, jego rola aksjomatu (a nie twierdzenia wynikającego z innych zasad) i możliwość stworzenia spójnych alternatywnych geometrii uczyniły z niego jeden z najważniejszych problemów w historii matematyki, wpływając na dalszy rozwój teorii i zastosowań geometrycznych.
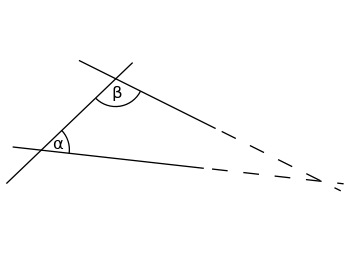
Jeżeli suma kątów wewnętrznych α (alfa) i β (beta) jest mniejsza niż 180°, to te dwie proste gdzieś się przetną, jeżeli obie zostaną przedłużone do nieskończoności.
Historia
Niektórzy matematycy uważali, że piąty postulat Euklidesa jest znacznie dłuższy i bardziej skomplikowany niż pozostałe cztery postulaty. Wielu z nich sądziło, że można go udowodnić z innych, prostszych aksjomatów. Niektórzy matematycy ogłosili, że dowiedli tego postulatu z prostszych postulatów, ale okazało się, że wszyscy się pomylili.
Aksjomat Playfaira
Inna, nowsza teza, znana jako aksjomat Playfaira, jest podobna do piątego postulatu Euklidesa. Mówi ono, że:
Biorąc pod uwagę prostą i punkt nie leżący na tej prostej, można narysować tylko jedną prostą przechodzącą przez ten punkt, która nie spotka się z drugą prostą.
W rzeczywistości matematycy odkryli, że aksjomat ten jest nie tylko podobny do piątego postulatu Euklidesa, ale ma dokładnie takie same implikacje. Z matematycznego punktu widzenia te dwie propozycje są nazywane propozycjami równoważnymi. Obecnie aksjomat Playfaira jest częściej używany przez matematyków niż oryginalny postulat równoległości Euklidesa.
Geometria nieeuklidesowa
W końcu niektórzy matematycy próbowali zbudować nowe geometrie bez użycia aksjomatu. Jeden z rodzajów geometrii nieeuklidesowej nazywany jest geometrią eliptyczną. W geometrii eliptycznej postulat równoległości jest zastąpiony aksjomatem, który mówi, że:
Biorąc pod uwagę prostą i punkt nie leżący na tej prostej, nie można narysować prostej przechodzącej przez ten punkt, która nie przetnie tej drugiej prostej.
Matematycy odkryli, że gdy zastąpili piąty postulat Euklidesa tym aksjomatem, nadal byli w stanie udowodnić wiele innych twierdzeń Euklidesa. Jednym ze sposobów wyobrażenia sobie geometrii eliptycznej jest myślenie o powierzchni kuli ziemskiej. Na kuli ziemskiej linie długości geograficznej wydają się równoległe na równiku, ale wszystkie spotykają się na biegunach. Pod koniec XIX wieku wykazano, że geometria eliptyczna jest spójna. Dowiodło to, że piąty postulat Euklidesa nie jest niezależny od pozostałych postulatów. Po tym wydarzeniu matematycy w większości zaprzestali prób udowodnienia piątego postulatu z pozostałych czterech postulatów. Zamiast tego, wielu matematyków zaczęło badać inne geometrie, które nie są zgodne z piątym postulatem Euklidesa.
Inny aksjomat, którym matematycy czasami zastępują piąty aksjomat Euklidesa, mówi, że:
Mając do dyspozycji prostą i punkt nie leżący na tej prostej, można narysować co najmniej dwie proste przechodzące przez ten punkt, które nie przetną drugiej prostej.
Nazywa się to geometrią hiperboliczną.
Inna geometria po prostu usuwa piąty postulat Euklidesa i nie zastępuje go niczym. Nazywa się to geometrią neutralną lub geometrią absolutną.
Przeszukaj encyklopedię