Regresja liniowa
Regresja liniowa jest sposobem na wyjaśnienie zależności między zmienną zależną a jedną lub kilkoma zmiennymi objaśniającymi za pomocą linii prostej. Jest to szczególny przypadek analizy regresji.
Regresja liniowa była pierwszym rodzajem analizy regresji, który był rygorystycznie badany. Wynika to z faktu, że modele, które zależą liniowo od swoich nieznanych parametrów, są łatwiejsze do dopasowania niż modele, które są nieliniowo powiązane z ich parametrami. Co więcej, właściwości statystyczne estymatorów wynikowych są łatwiejsze do określenia.
Regresja liniowa ma wiele praktycznych zastosowań. Większość zastosowań należy do jednej z dwóch szerokich kategorii:
- Regresja liniowa może być stosowana w celu dopasowania modelu predykcyjnego do zbioru obserwowanych wartości (danych). Jest to przydatne, jeśli celem jest przewidywanie, prognozowanie lub redukcja. Po opracowaniu takiego modelu, jeśli następnie zostanie podana dodatkowa wartość X bez towarzyszącej jej wartości y, to dopasowany model może być użyty do przewidywania wartości y.
- Biorąc pod uwagę zmienną y oraz szereg zmiennych X1, ..., Xp, które mogą być związane z y, analizę regresji liniowej można zastosować do ilościowego określenia siły związku między y a Xj, do oceny, który Xj nie ma żadnego związku z y, oraz do określenia, które podzbiory Xj zawierają zbędne informacje o y.
Modele regresji liniowej starają się, aby odległość pionowa pomiędzy linią a punktami danych (np. resztami) była jak najmniejsza. Nazywa się to "dopasowaniem linii do danych" (ang. fitting the line to the data). Często modele regresji liniowej starają się minimalizować sumę kwadratów reszt (najmniej kwadratów), ale istnieją inne sposoby dopasowania. Obejmują one minimalizowanie "braku dopasowania" w jakiejś innej normie (jak w przypadku regresji z najmniejszymi odchyleniami absolutnymi) lub minimalizowanie karanej wersji funkcji utraty najmniejszych kwadratów, jak w przypadku regresji grzbietowej. Metoda najmniejszych kwadratów może być również stosowana do dopasowania modeli, które nie są liniowe. Jak przedstawiono powyżej, terminy "najmniej kwadratów" i "model liniowy" są ściśle powiązane, ale nie są one synonimami.
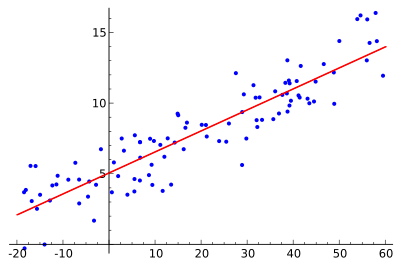
Chodzi o to, aby znaleźć czerwoną krzywą, niebieskie punkty to prawdziwe próbki. Za pomocą regresji liniowej wszystkie punkty można połączyć za pomocą jednej, prostej linii. Ten przykład wykorzystuje prostą regresję liniową, gdzie kwadrat odległości między czerwoną linią a każdym punktem próbki jest zminimalizowany.
Zastosowanie
Ekonomia
Regresja liniowa jest głównym narzędziem analitycznym w ekonomii. Na przykáad jest ona wykorzystywana do odgadywania wydatków konsumpcyjnych, wydatków na inwestycje staáe, inwestycji w zapasy, zakupu krajowego eksportu, wydatków na import, popytu na posiadanie aktywów páynnych, popytu na pracĊ i podaĪy pracy.
Pytania i odpowiedzi
P: Co to jest regresja liniowa?
O: Regresja liniowa to sposób na sprawdzenie za pomocą matematyki, jak coś się zmienia, gdy zmieniają się inne rzeczy. Wykorzystuje zmienną zależną i jedną lub więcej zmiennych objaśniających, aby stworzyć linię prostą, zwaną "linią regresji".
P: Jakie są zalety regresji liniowej?
O: Modele, które zależą liniowo od swoich nieznanych parametrów, są łatwiejsze do dopasowania niż modele, które są nieliniowo związane ze swoimi parametrami. Ponadto łatwiej jest określić właściwości statystyczne otrzymanych estymatorów.
P: Jakie są niektóre praktyczne zastosowania regresji liniowej?
O: Regresję liniową można wykorzystać do dopasowania modelu predykcyjnego do obserwowanych wartości (danych) w celu dokonania przewidywań, prognoz lub redukcji. Można ją również wykorzystać do ilościowego określenia siły związków między zmiennymi i identyfikacji podzbiorów danych, które zawierają zbędne informacje o innej zmiennej.
P: W jaki sposób modele regresji liniowej starają się minimalizować błędy?
O: Modele regresji liniowej starają się, aby pionowa odległość między linią a punktami danych (resztami) była jak najmniejsza. W tym celu minimalizuje się sumę kwadratów reszt (najmniejsze kwadraty), brak dopasowania w innej normie (najmniejsze odchylenia bezwzględne) lub minimalizuje się karaną wersję funkcji straty najmniejszych kwadratów (regresja grzbietowa).
P: Czy jest możliwe, aby modele regresji liniowej nie były oparte na najmniejszych kwadratach?
O: Tak, możliwe jest, aby modele regresji liniowej nie opierały się na metodzie najmniejszych kwadratów, lecz stosowały takie metody, jak minimalizacja braku dopasowania w innej normie (najmniejsze odchylenie bezwzględne) lub minimalizacja karnej wersji funkcji straty najmniejszych kwadratów (regresja grzbietowa).
P: Czy "model liniowy" i "najmniejszy kwadrat" to synonimy?
O: Nie, to nie są synonimy. Chociaż są blisko spokrewnione, "model liniowy" odnosi się do linii prostej, natomiast "najmniejszy kwadrat" odnosi się do próby zminimalizowania błędów poprzez upewnienie się, że między linią a punktami danych jest minimalna odległość w pionie.
Przeszukaj encyklopedię