Zegar świetlny

Zegar świetlny to prosty sposób na pokazanie podstawowej cechy Szczególnej względności. Zegar jest przeznaczony do pracy poprzez odbijanie błysku światła od odległego lustra i wykorzystanie jego powrotu do wyzwalania kolejnego błysku światła, przy jednoczesnym liczeniu, ile błysków wystąpiło po drodze. Łatwo jest pokazać, że osoby na Ziemi obserwujące statek kosmiczny lecący nad nami z takim zegarem widziałyby jak tyka on stosunkowo wolno. Efekt ten nazywany jest dylatacjączasu.

Zanim zbadamy zegar świetlny, rozważmy inny rodzaj względności. Wyobraźmy sobie, że ktoś dryfuje piłkę do koszykówki w ładowni dużego odrzutowca towarowego. Koszykarz porusza się w tym samym kierunku co samolot odrzutowy. Pozostałe osoby w samolocie widzą, jak porusza się na metr lub dwa, gdy jeden z nich dryfuje. Między pierwszym odbijaniem piłki a drugim odbijaniem, minęła około jedna sekunda. Ale kiedy nastąpiło pierwsze odbicie, koszykówka znajdowała się nad Gibraltarem, a kiedy nastąpiło drugie odbicie, koszykówka znajdowała się nad wodą bliżej Hiszpanii. Więc koszykówka przesunęła się o 280 metrów w stosunku do Ziemi.

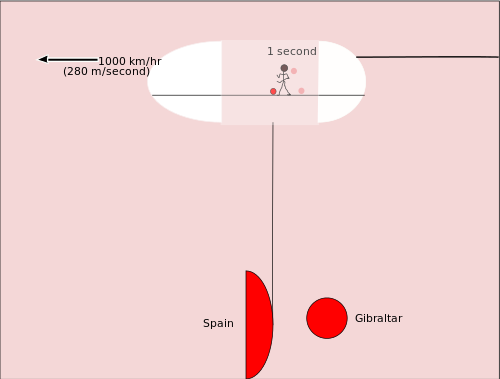
Teraz rozważmy nieco podobną kwestię ruchu względnego. Tym razem rozważymy co ludzie patrząc na gwiazdy z Bieguna Północnego widzą gdy przelatuje nad nimi bardzo szybki statek kosmiczny. Możemy użyć algebry i pitagorejskiego twierdzenia do obliczenia, ile czasu zwalnia na statku kosmicznym. Jedyną inną rzeczą, której potrzebujemy, jest równanie, które odnosi się do odległości, d, tempa lub prędkości podróży, r, i czasu, t:

d = rt

Prędkość światła jest stała, więc zastosujemy tę wartość do dwóch problemów. Prędkość światła nazwiemy c, ponieważ jest to litera, którą naukowcy zwykle używają do jej określenia.

Zegar wykonywany jest poprzez umieszczenie w dolnej części długiego bieguna strumienia światła, lustra na górze bieguna oraz elektronicznego detektora światła w dolnej części bieguna. Zegar uruchamia się przez krótkie zamknięcie wyłącznika, który wysyła jedno mrugnięcie światła z dołu słupa na górę słupa, gdzie jest ono odbijane z powrotem na dół słupa. Gdy detektor światła na dole słupa zauważy mrugnięcie światła, robi dwie rzeczy. Dodaje jedną do licznika, który jest do niego przymocowany, i wystrzeliwuje kolejne mrugnięcie światła do lustra. Kiedy to mrugnięcie światła wraca na dno, liczba zmienia się na dwie, a kolejne mrugnięcie światła zostaje uruchomione. Ponieważ światło przemieszcza się bardzo szybko (300.000 km/sekundę), na każdą sekundę mierzoną przez zwykły zegar, zegar świetlny "tyka" bardzo dużą ilość razy.

Aby ułatwić matematykę, powiemy, że kij ma pół kilometra długości. Więc jeśli staniemy przy zegarze świetlnym, który jest zbudowany obok dużej lunety na biegunie północnym, zobaczymy, że światło przechodzi jeden kilometr na każdy "tick" zegara świetlnego. Ponieważ przebyta odległość, d, równa się prędkości pomnożonej przez czas, a chodzi o prędkość c, mamy to równanie:

d = ct

i możemy rozwiązać to równanie dla t, aby dowiedzieć się, jak długo w sekundach każdy "tick" jest.

1 km = 300 000 km/sekundę * t sekund

t sekunda = 1 km/300 000 (km/sekundę) = 1/300 000 sekund = 0,00000333...3 sekundy

Innymi słowy, każde "tyknięcie" zegara świetlnego zajmie 0,00000333...3 sekundy.

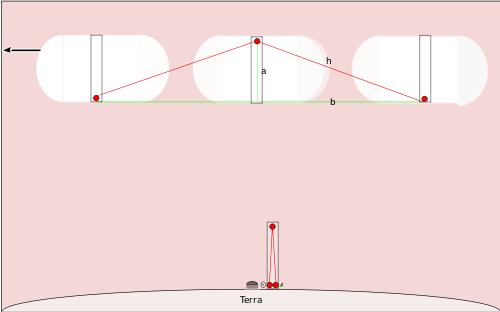
Gdyby statek kosmiczny leciał po linii prostej przechodzącej nad biegunem północnym z dużą cząstką prędkości światła i miał podobny zegar, ludzie obserwujący jego przejazd zobaczyliby, że lustro na górze bieguna przesunęło się od razu nad emitującym światło, więc światło podróżowałoby wzdłuż linii oznaczonej h na wykresie, a następnie podążałoby za drugą hipotenezą z powrotem w dół do podstawy bieguna - która już by się przesunęła, ponieważ statek kosmiczny porusza się tak szybko. Możemy dowiedzieć się, ile czasu trwałby jeden kleszcz według ludzi na Ziemi. Wiemy, że biegun statku kosmicznego ma długość jednego metra, ponieważ jest to ten sam rodzaj zegara, którego ludzie używają na Biegunie Północnym. Chcemy obliczyć t' , czas potrzebny do wykonania jednego tyknięcia zegara na statku kosmicznym.

Wiemy, że statek kosmiczny będzie podróżował 1/2 r t' podczas gdy mrugnięcie światła skierowane jest w górę w kierunku lustra, a kolejne 1/2 r t' podczas gdy mrugnięcie światła skierowane jest w dół w kierunku podstawy słupa. Tak więc wyliczenie to daje nam długość linii b na wykresie. Znamy a, więc możemy obliczyć h według twierdzenia Pitagorejczyka:

h = √(a2 + (rt' /2)²)

Zatem całkowita odległość, jaką pokonuje światło, wynosi 2 h lub d = 2 √(a2 + (rt' /2)²).

Wiemy też, że prędkość światła, c, jest stała. Bez względu na to, kto ją mierzy, okazuje się, że jest to ta sama prędkość. Możemy więc wykorzystać ten fakt do innego sposobu obliczenia, jak długo trwa błysk światła od podstawy do górnej części słupa i z powrotem:

t' = d/c

Innymi słowy, d = c t' .

Więc możemy napisać

c t' = 2 √(a2 + (rt' /2)²)

lub

1/2 c t' = √(a2 + (rt' /2)²)

Aby rozwiązać powyższe równanie, będziemy musieli:

1. Kwadrat po obu stronach
2. Podzielić obie strony przez t' ²
3. Pomnożyć obie strony przez 4
4. Podzielić obie strony przez c2
5. Uprościć c2 / c2
6. Odejmij r2/c2 z obu stron
7. Weźmy pierwiastek kwadratowy z obu stron
8. Pomnożyć obie strony przez t'
9. Podzielić obie strony przez √(1-r2/c2)

Rozwiązując powyższe równanie stwierdzamy, że:

t" = 2a/(c√(1-r2/c2)

Czas pomiędzy kliknięciami na zegarze na biegunie północnym wynosi 2a/c, więc możemy wtedy pisać:

t' = t/√(1-r2/c2)

Jeżeli t = 1 sekunda, to jeżeli statek kosmiczny porusza się z połową prędkości światła, t' = 1,1547 sek.

Eksperyment z różnymi prędkościami podróżowania na stronie: http://www.1728.org/reltivty.htm

Pytania i odpowiedzi

P: Co to jest dzwonek świetlny?

P: Co to jest dylatacja czasu?

P: Jak można obliczyć, jak bardzo czas zwalnia w statku kosmicznym?

P: Jak działa zegar świetlny?

P: Jakie równanie jest potrzebne do tego obliczenia?

P. Jak twierdzenie Pitagorasa odnosi się do tego obliczenia?

Szukaj według litery