Równanie Younga–Laplace'a (prawo Laplace'a): definicja i zastosowania
Równanie Younga–Laplace'a (prawo Laplace'a): definicja, matematyka i praktyczne zastosowania w fizyce, inżynierii i medycynie — napięcie powierzchniowe i ciśnienie kapilarne.
W fizyce równanie Young-Laplace'a (/ləˈplɑːs/) opisuje skok ciśnienia między dwiema fazami spowodowany napięciem powierzchniowym. Jest to nieliniowe, częściowe równanie różniczkowe, które łączy różnicę ciśnień z krzywizną powierzchni rozdzielającej dwa płyny statyczne, na przykład wodę i powietrze. Różnica ta wynika ze zjawiska napięcia powierzchniowego (czasem zwanego też napięciem ściany dla bardzo cienkich ścian). Równanie Young-Laplace'a jest podstawowym narzędziem w opisie powierzchni kapilarnych i kształtów kropli oraz pęcherzyków.
W fizjologii jest to znane jako prawo Laplace'a. Jest ono używane do opisania zależności między ciśnieniem, promieniem i napięciem ściany w pustych organach (np. naczynia krwionośne, pęcherzyki płucne).
Równanie i interpretacja
Ogólna postać równania Young-Laplace'a wyraża skok ciśnienia Δp przez napięcie powierzchniowe γ i sumę odwrotności dwóch głównych promieni krzywizny R1 i R2 powierzchni:
Δp = p_in – p_out = γ (1/R1 + 1/R2)
Alternatywnie, korzystając z pojęcia średniej krzywizny H = (1/2)(1/R1 + 1/R2), zapisuje się też
Δp = 2 γ H
Jednostki: γ w N/m, Δp w Pa, krzywizna w 1/m. Znak skoku ciśnienia zależy od orientacji normalnej do powierzchni — przyjmuje się zwykle, że wypukłość w stronę fazy wewnętrznej daje dodatni wkład krzywizny.
Przykłady szczególne
- Kula (kropla lub pęcherzyk sferyczny): R1 = R2 = R → Δp = 2γ / R. Dla kropli lub pęcherzyka o promieniu 1 mm i γ(woda–powietrze) ≈ 0,072 N/m otrzymujemy Δp ≈ 144 Pa.
- Walec (np. cienki pęcherzyk wzdłuż osi): jeśli jedna krzywizna ≈ 0 i druga = R → Δp = γ / R.
- Kapilara w rurce (ciśnienie kapilarne): przy zanurzeniu cienkiej rurki o promieniu r ciecz podnosi się do wysokości h, gdzie siły napięcia równoważą ciężar słupa cieczy. W uproszczeniu:
h = 2 γ cos θ / (ρ g r),
gdzie θ to kąt zwilżania, ρ g przyspieszenie grawitacyjne pomnożone przez gęstość cieczy. W praktyce często używa się uproszczonego wzoru na ciśnienie kapilarne w porach: Δp = 2 γ cos θ / r.
Warunki brzegowe i kąt zwilżania
Równanie Young-Laplace'a opisuje lokalne równanie równowagi sił przy powierzchni, natomiast kształt powierzchni zależy również od warunków brzegowych, zwłaszcza od kąta zwilżania θ między powierzchnią stałą a cieczą. Kąt ten związany jest z równaniem Younga:
γ_SV − γ_SL = γ_LV cos θ
(gdzie γ_SV, γ_SL, γ_LV to odpowiednio napięcia powierzchniowe między stałą a parą, stałą a cieczą oraz cieczą a parą).
Zastosowania
- Opis kształtu kropli i pęcherzyków, stabilność pęcherzyków i emulsji.
- Kapilarność: podnoszenie cieczy w cienkich rurkach, przesiąkanie w porowatych materiałach, procesy w glebie i papierze.
- Inżynieria mikrofluidyczna i druk atramentowy (inkjet): kształt menisku i ciśnienie wewnątrz kropli determinują zachowanie płynów na małych skalach.
- Fizjologia i medycyna: prawo Laplace'a stosowane do naczyń krwionośnych i pęcherzyków płucnych — relacja między ciśnieniem transmuralnym, napięciem ściany i promieniem (daje wyjaśnienie np. dlaczego większe naczynia wymagają innego napięcia, a małe pęcherzyki są bardziej podatne na zapadanie się bez surfaktantu).
- Technologie powierzchniowe: tworzenie powłok, zwilżalność materiałów, projektowanie struktur superhydrofobowych.
Ograniczenia i założenia
- Równanie Young-Laplace'a dotyczy równowagi statycznej (brak przepływu masy lub przy przepływie o małym wpływie dynamicznym).
- Zakłada jednorodność i izotropowość napięcia powierzchniowego — w obecności gradientów napięcia (efekt Marangoniego) lub surfaktantów jego postać i rozwiązania się zmieniają.
- Grawitacja może znacząco modyfikować kształt dużych kropli i pęcherzyków; wtedy trzeba łączyć równanie Young-Laplace'a z równaniem hydrostatycznym.
- Przy bardzo małych skalach (nanoskala) dodatkowe efekty, jak linia kontaktu czy struktury molekularne, mogą wymagać korekt.
Krótka historia
Równanie nosi imię Thomasa Younga, który opracował jakościową teorię napięcia powierzchniowego w 1805 roku, oraz Pierre'a-Simona Laplace'a, który uzupełnił opis matematyczny w następnym roku. Czasami bywa też nazywane równaniem Young-Laplace'a-Gaussa: Carl Friedrich Gauss ujednolicił prace Younga i Laplace'a w 1830 roku, wyprowadzając równanie różniczkowe i warunki brzegowe korzystając z zasad pracy wirtualnej Johanna Bernoullego.
Równanie Young-Laplace'a pozostaje jednym z podstawowych narzędzi w mechanice płynów przy badaniu zjawisk powierzchniowych — od skali makro (menisku w rurce) po zastosowania mikroskopowe i biologiczne.
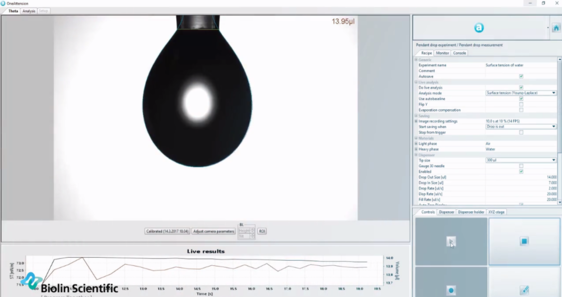
Tensjometry optyczne wykorzystują równanie Young-Laplace'a do automatycznego określania napięcia powierzchniowego cieczy w oparciu o kształt wiszącej kropli.
Pytania i odpowiedzi
P: Co to jest równanie Younga-Laplace'a?
O: Równanie Younga-Laplace'a to nieliniowe równanie różniczkowe cząstkowe, które opisuje różnicę ciśnienia kapilarnego na granicy dwóch statycznych płynów, takich jak woda i powietrze.
P: Do czego odnosi się to równanie?
O: Odnosi się do różnicy ciśnień do kształtu powierzchni lub ściany.
P: Kto opracował tę teorię?
O: Teoria została opracowana przez Thomasa Younga w 1805 roku, a Pierre-Simon Laplace ukończył jej matematyczny opis w następnym roku. Później, w 1830 roku, ujednolicił ją Carl Friedrich Gauss.
P: Jak się ją wykorzystuje w fizjologii?
O: W fizjologii znane jest jako prawo Laplace'a i służy do opisu ciśnienia wewnątrz pustych organów.
P: Jakie zjawisko wyjaśnia?
A: Równanie Younga-Laplace'a wyjaśnia zjawisko napięcia powierzchniowego lub napięcia ścian.
P: Czy napięcie ścienne ma zastosowanie w przypadku grubych ścian? O: Nie, napięcie ścienne można stosować tylko w przypadku bardzo cienkich ścian.
Przeszukaj encyklopedię