Okrąg jednostkowy — definicja, równanie i zastosowania w trygonometrii

Poznaj okrąg jednostkowy — definicję, równanie x²+y²=1 oraz praktyczne zastosowania w trygonometrii. Przykłady, intuicyjne objaśnienia i zastosowania krok po kroku.

Autor: Leandro Alegsa

21-03-2026 14:36

W matematyce okrąg jednostkowy to okrąg o promieniu 1. Równanie okręgu jednostkowego ma postać x 2 + y 2 = 1 {{displaystyle x^{2}+y^{2}=1}} $x^{2}+y^{2}=1$ . Okrąg jednostkowy ma środek w punkcie początkowym, czyli na współrzędnych (0,0). Jest on często używany w trygonometrii.

Definicja i podstawowe własności

Okrąg jednostkowy to zbiór punktów (x,y) w płaszczyźnie kartezjańskiej spełniających równanie x² + y² = 1. Jego środek leży w punkcie (0,0), promień r = 1. Do najważniejszych wielkości należą:

Obwód: 2π·1 = 2π.
Pole powierzchni koła o promieniu 1 (jeśli rozważamy wnętrze): π·1² = π.
Symetrie: symetryczny względem osi OX i OY oraz względem początku układu współrzędnych.

Postać parametryczna i orientacja

Każdy punkt na okręgu jednostkowym można zapisać parametrycznie za pomocą kąta θ mierzonego od dodatniej półosi OX:

x = cos θ, y = sin θ.

Przy wzroście θ punkt porusza się po okręgu w kierunku przeciwnym do ruchu wskazówek zegara (orientacja standardowa). W zapisie parametrycznym pochodna wektora pozycji daje wektor styczny: (dx/dθ, dy/dθ) = (−sin θ, cos θ).

Trygonometria — współrzędne punktów i kluczowe kąty

W trygonometrii okrąg jednostkowy pozwala zdefiniować funkcje sinus i cosinus dla dowolnego kąta. Punkt odpowiadający kątowi θ ma współrzędne (cos θ, sin θ). Dla najważniejszych kątów wartości są:

θ = 0: (1, 0)
θ = π/6 (30°): (√3/2, 1/2)
θ = π/4 (45°): (√2/2, √2/2)
θ = π/3 (60°): (1/2, √3/2)
θ = π/2 (90°): (0, 1)

Symetrie okręgu pomagają też wyznaczać wartości funkcji trygonometrycznych dla kątów w II, III i IV ćwiartce (zmiany znaków współrzędnych).

Tożsamości wynikające z równania okręgu

Bezpośrednią konsekwencją równania okręgu jest podstawa wielu tożsamości trygonometrycznych:

cos²θ + sin²θ = 1 (tożsamość pitagorejska)
z niej wynikają: 1 + tan²θ = sec²θ oraz cot²θ + 1 = csc²θ (tam, gdzie funkcje są określone).

Zastosowania okręgu jednostkowego

Definicja funkcji trygonometrycznych dla wszystkich kątów (nie tylko tych ostrych).
Rozwiązywanie równań i nierówności trygonometrycznych oraz analizowanie okresowości funkcji sin i cos.
Analiza fazy i amplitudy w fizyce fal oraz elektrotechnice.
Reprezentacja obrotów w płaszczyźnie: macierz obrotu o kąt θ ma elementy oparte na cos θ i sin θ.
W teorii liczb i analizie zespolonej — powiązanie z liczbami zespolonymi i wykładniczą formą Eulera.

Okrąg jednostkowy w płaszczyźnie zespolonej i wzór Eulera

W płaszczyźnie zespolonej punkt na jednostkowym okręgu odpowiada liczbie zespolonej o module 1. Wzór Eulera łączy funkcje trygonometryczne z wykładnikiem zespolonym:

e^iθ = cos θ + i sin θ.

To odwzorowanie jest użyteczne przy opisie rotacji, szeregu Fouriera oraz rozwiązywaniu równań różniczkowych.

Praktyczne wskazówki

Kąty mierzone w radianach są naturalne przy pracy z okręgiem jednostkowym (pełny obrót = 2π rad).
Ujemne kąty oznaczają przesunięcie zgodne z ruchem wskazówek zegara.
Aby znaleźć wartość funkcji trygonometrycznej danego kąta, można odczytać współrzędne odpowiedniego punktu na okręgu.

Okrąg jednostkowy to podstawowe narzędzie w trygonometrii i analizie matematycznej — pozwala wizualizować funkcje trygonometryczne, rozumieć ich własności oraz łączyć geometrię z analizą i algebrą zespoloną.

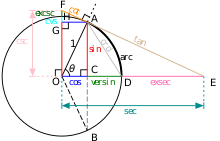
Koło jednostkowe może być użyte do modelowania każdej funkcji trygonometrycznej.

Funkcje trygonometryczne w kole jednostkowym

Na okręgu jednostkowym, gdzie t {t} $t$ jest pożądanym kątem, x {displaystyle x} i y {displaystyle y} można zdefiniować jako cos ( t ) = x {displaystyle cos(t)=x} $\cos(t)=x$ i sin ( t ) = y {displaystyle sin(t)=y} $\sin(t)=y$ . Korzystając z funkcji okręgu jednostkowego, x 2 + y 2 = 1 {displaystyle x^{2}+y^{2}=1}}. $x^{2}+y^{2}=1$ , znajdujemy kolejne równanie dla okręgu jednostkowego, cos 2 ( t ) + sin 2 ( t ) = 1 {displaystyle cos ^{2}(t)+sin ^{2}(t)=1}} $\cos ^{2}(t)+\sin ^{2}(t)=1$ . Przy pracy z funkcjami trygonometrycznymi warto posługiwać się głównie kątami o miarach od 0 do π 2 {displaystyle ^pi ^2} $\pi \over 2$ radianów, czyli od 0 do 90 stopni. Możliwe jest jednak uzyskanie większych kątów. Korzystając z okręgu jednostkowego, można znaleźć dwie tożsamości: cos ( t ) = cos ( 2 ⋅ π k + t ) {cos(t)=cos(2) } $\cos(t)=\cos(2\cdot \pi k+t)$ oraz s i n ( t ) = sin ( 2 ⋅ π k + t ) {displaystyle sin(t)=sin(2) } $sin(t)=\sin(2\cdot \pi k+t)$ dla dowolnej liczby całkowitej k {displaystyle k} .

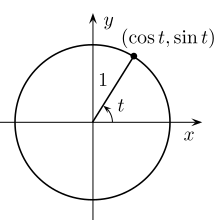
Koło jednostkowe może zastąpić zmienne dla funkcji trygonometrycznych.

Pytania i odpowiedzi

P: Co to jest okrąg jednostkowy?

O: Okrąg jednostkowy to okrąg o promieniu 1.

P: Jakie jest równanie okręgu jednostkowego?

O: Równanie okręgu jednostkowego ma postać x^2 + y^2 = 1.

P: Gdzie znajduje się środek okręgu jednostkowego?

O: Środek okręgu jednostkowego znajduje się w punkcie początkowym, czyli we współrzędnych (0,0).

P: Do czego służy okrąg jednostkowy w matematyce?

O: Okrąg jednostkowy jest często używany w trygonometrii.

P: Dlaczego okrąg jednostkowy jest ważny?

O: Okrąg jednostkowy jest ważny, ponieważ pomaga w zrozumieniu zależności między kątami i funkcjami trygonometrycznymi.

P: Jaki jest promień okręgu jednostkowego?

O: Promień okręgu jednostkowego wynosi 1.

P: Jakie znaczenie ma to, że promień okręgu jednostkowego wynosi 1?

O: Znaczenie promienia okręgu jednostkowego równego 1 polega na tym, że upraszcza on obliczenia i ułatwia powiązanie kątów z wartościami trygonometrycznymi.

Przeszukaj encyklopedię