Funkcja skokowa Heaviside’a

Funkcja Heaviside'a, H jest funkcją nieciągłą, której wartość wynosi zero dla wejścia ujemnego i jeden dla wejścia dodatniego.

Funkcja ta jest używana w matematyce teorii sterowania do reprezentowania sygnału, który włącza się w określonym czasie i pozostaje włączony na czas nieokreślony. Została ona nazwana na cześć Anglika Olivera Heaviside'a.

Funkcja Heaviside'a jest całką z funkcji delta Diraca: H′ = δ. Zapisuje się ją czasami jako

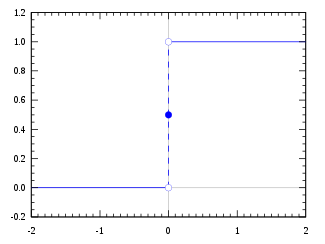
Funkcja kroku Heaviside'a, wykorzystująca konwencję połowy maksimum

Forma dyskretna

Możemy również zdefiniować alternatywną postać funkcji stopnia Heaviside'a jako funkcję zmiennej dyskretnej n:

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {displaystyle H[n]={begin{cases}0,&n<0,&n<1,&n<0,&n<0,&end{cases}}. $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

gdzie n jest liczbą całkowitą.

Lub

H ( x ) = lim z → x - ( ( | z | / z + 1 )/2 ) { {przykład H(x)= ((|z|/z+1)/2)} $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

Impuls jednostkowy czasu dyskretnego jest pierwszą różnicą kroku czasu dyskretnego

δ [ n ] = H [ n ] - H [ n - 1 ] . = H[n] - H[n-1]. } $\delta \left[n\right]=H[n]-H[n-1].$

Funkcja ta jest sumą kumulatywną delty Kroneckera:

H [ n ] = ∑ k = - ∞ n δ [ k ] {{displaystyle H[n]=suma _{k=-infty }^{n}delta [k]} $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

gdzie

δ [ k ] = δ k , 0 {{displaystyle \delta [k]= δ k , 0 {{k,0}} $\delta [k]=\delta _{k,0}\,$

jest dyskretną funkcją impulsu jednostkowego.

Reprezentacje

Często przydatna jest całkowa reprezentacja funkcji kroku Heaviside'a:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ ∞ 1 τ - i ϵ e i x τ d τ . {displaystyle H(x)=lim _{epsilon \ do 0^{+}}-{1 \powyżej 2 \i \i \mathrm {i} }int _{-epsilon }^{1 \\\\\\\\\\ \\epsilon } \mathrm {e} ^{- ^mathrm {i} xtau } ^{mathrm {d} \tau = \lim _{epsilon \ do 0^{+}}{1 \powyżej 2 \i \mathrm {i} \\}int _{- \infty }^{1 \infty }}{1 \over \tau - \mathrm {i} ^ ^ ^ ^ ^ ^ epsilon } ^{mathrm {i} xtau } ^{mathrm {d} . } $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

Wartość funkcji w punkcie 0 może być określona jako H(0) = 0, H(0) = ½ lub H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

Powiązane strony

Transformacja Laplace'a

Pytania i odpowiedzi

P: Co to jest funkcja Heaviside'a?

O: Funkcja Heaviside'a jest nieciągłą funkcją, której wartość wynosi zero dla ujemnych danych wejściowych i jeden dla dodatnich danych wejściowych.

P: Dlaczego funkcja Heaviside'a jest używana w teorii sterowania?

Funkcja Heaviside'a jest używana w teorii sterowania do reprezentowania sygnału, który włącza się w określonym czasie i pozostaje włączony przez czas nieokreślony.

P: Od kogo pochodzi nazwa funkcji Heaviside'a?

O: Funkcja Heaviside'a została nazwana na cześć Anglika Olivera Heaviside'a.

P: Jaki jest związek między funkcją Heaviside'a a funkcją delta Diraca?

O: Funkcja Heaviside'a jest całką z funkcji delta Diraca: H′(x)= δ(x).

P: Co daje funkcja Heaviside'a dla dodatnich wartości wejściowych?

O: Funkcja Heaviside'a daje wynik jeden dla dodatnich wartości wejściowych.

P: Jakie jest wyjście funkcji Heaviside'a dla ujemnych wartości wejściowych?

O: Funkcja Heaviside'a daje zero dla ujemnych wartości wejściowych.

P: Jakim typem funkcji jest funkcja Heaviside'a?

O: Funkcja Heaviside'a jest funkcją nieciągłą.