Theorema Egregium
Twierdzenie Gaussa (łac. Theorema Egregium) to ważny wynik geometrii różniczkowej udowodniony przez Carla Friedricha Gaussa. Twierdzenie dotyczy krzywizny powierzchni. Twierdzenie mówi, że krzywiznę można wyznaczyć mierząc kąty, odległości i ich współczynniki na samej powierzchni. Nie ma potrzeby mówić o szczególnym sposobie, w jaki powierzchnia jest osadzona w otaczającej ją trójwymiarowej przestrzeni euklidesowej. Innymi słowy, krzywizna gaussowska powierzchni nie zmienia się, jeśli zginamy powierzchnię bez jej rozciągania.
Gauss przedstawił to twierdzenie w taki sposób (w tłumaczeniu z łaciny):
Z tego powodu wzór z poprzedniego artykułu prowadzi do znamiennego twierdzenia. Jeśli zakrzywiona powierzchnia jest rozwinięta na jakiejkolwiek innej powierzchni, to miara krzywizny w każdym punkcie pozostaje niezmieniona.
Twierdzenie jest "godne uwagi", ponieważ wyjściowa definicja krzywizny gaussowskiej bezpośrednio wykorzystuje położenie powierzchni w przestrzeni. Jest więc dość zaskakujące, że wynik nie zależy od jej osadzenia, pomimo wszystkich poddanych deformacji zginających i skręcających.
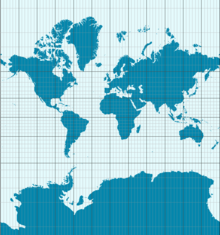
Konsekwencją Theorema Egregium jest to, że Ziemia nie może być wyświetlana na mapie bez zniekształceń. Projekcja Merkatora, pokazana tutaj, zachowuje kąty, ale zmienia powierzchnię. Na przykład, Antarktyda jest przedstawiona jako znacznie większa niż jest w rzeczywistości.
Pytania i odpowiedzi
P: Czym jest Theorema Egregium Gaussa?
O: Teoremat Egregium Gaussa to główny wynik geometrii różniczkowej dotyczący krzywizny powierzchni, udowodniony przez Carla Friedricha Gaussa.
P: W jaki sposób można wyznaczyć krzywiznę zgodnie z twierdzeniem Gaussa?
O: Zgodnie z Theorema Egregium Gaussa, krzywiznę można wyznaczyć mierząc kąty, odległości i ich prędkości na samej powierzchni.
P: Czy konieczne jest mówienie o szczególnym sposobie, w jaki powierzchnia jest osadzona w otaczającej ją trójwymiarowej przestrzeni euklidesowej, aby określić krzywiznę?
O: Nie, nie jest konieczne mówienie o szczególnym sposobie, w jaki powierzchnia jest osadzona w otaczającej ją trójwymiarowej przestrzeni euklidesowej, aby określić krzywiznę zgodnie z Theorema Egregium Gaussa.
P: Czy gaussowska krzywizna powierzchni zmienia się, jeśli zginamy powierzchnię bez jej rozciągania?
O: Nie, krzywizna gaussowska powierzchni nie zmienia się, jeśli zginamy powierzchnię bez jej rozciągania zgodnie z twierdzeniem Gaussa Egregium.
P: Kto przedstawił twierdzenie w ten sposób?
O: Gauss przedstawił twierdzenie w ten sposób.
P: Czym wyróżnia się to twierdzenie?
O: Twierdzenie jest "niezwykłe", ponieważ początkowa definicja krzywizny gaussowskiej bezpośrednio wykorzystuje położenie powierzchni w przestrzeni. Jest więc dość zaskakujące, że wynik nie zależy od jej osadzenia, pomimo wszystkich poddanych zginaniu i skręcaniu deformacji.
P: W jaki sposób Gauss przedstawił to twierdzenie?
O: Gauss przedstawił twierdzenie w taki sposób, że jeśli zakrzywiona powierzchnia jest rozwinięta na dowolnej innej powierzchni, miara krzywizny w każdym punkcie pozostaje niezmieniona.
Przeszukaj encyklopedię